лекции / В. А. Бородавкин, И. Л. Петрова -ТАУ дискретных систем / 9 Лекция

5

Лекция 9.

Устойчивость импульсных систем.

9.1 Условия устойчивости.

Анализ устойчивости дискретной системы управления является важным этапом при определении работоспособности системы управления. Так же как и в случае непрерывных линейных систем, дискретная система управления называется устойчивой, если ее переходная функция остается ограниченной при любых ограниченных по абсолютной величине входных возмущениях. Поэтому для определения устойчивости ДАС можно воспользоваться разностным уравнением, описывающим поведение системы.

Динамика переходного процесса в замкнутой импульсной системе может быть описана разностными уравнениями первого порядка в виде

……………………………………

где n – безразмерное время, выражаемое порядковым номером импульсов (n=1,2,..); m – порядок системы разностных уравнений; - первая разность (аналог первой производной в дифференциальных уравнениях).

Характеристическое уравнение для этой системы записывается в виде

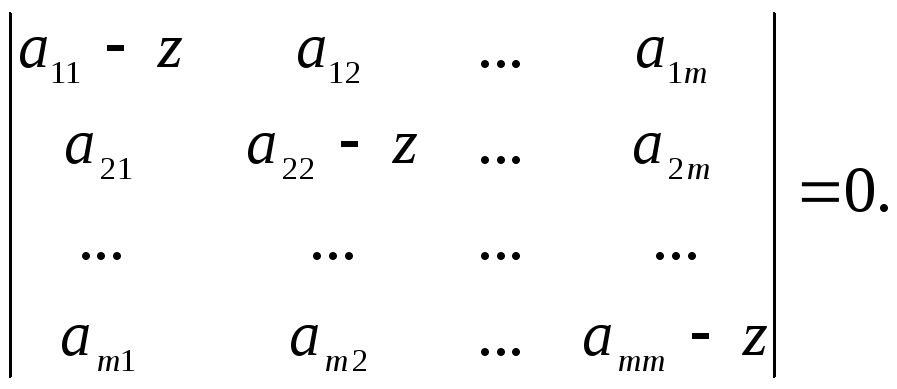
Вместо системы в разностных уравнений первого порядка можно записать одно разностное уравнение высокого порядка

с характеристическим уравнением

(1)

Процесс, протекающий в дискретной системе, может быть представлен двумя составляющими – собственными и вынужденными движениями. Первая составляющая определяет устойчивость системы и вычисляется в результате общего решения однородного разностного уравнения (1).

По аналогии с непрерывными системами, если

(2)

то ДАС будет устойчивой.

Решение разностного уравнения (когда корни простые) имеет вид

(3)

где z_i - корни характеристического уравнения (i=1,2,…,m) и

причем являются полюсами передаточной функции замкнутой импульсной системы Ф^* (q).

Из решения (3) видно, что для устойчивости импульсной системы необходимо и достаточно, чтобы все корни характеристического уравнения замкнутой дискретной системы (как известно из теории разностных уравнений), были по модулю меньше единицы. Следовательно, необходимым и достаточным условием устойчивости ДАС является соблюдение неравенства

(4)

Если хотя бы один корень система будет неустойчивой.

9.2 Границы устойчивости. Области устойчивости.

Значением кого-либо корня при всех остальных определяется граница устойчивости импульсной системы.

Следовательно, геометрически область устойчивости системы на плоскости корней z изобразится единичным кругом (рис.1), т.е. границей устойчивости является окружность единичного радиуса.

z

W

Im

Im

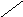
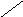
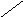
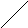
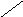-1 1

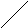
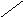
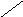Re Re

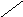
Рис.1 Рис.2

Если применить w-преобразование

(5)

то этот круг отобразится в левую полуплоскость w (рис.2).

Подставив (5) в характеристическое уравнение импульсной системы (1),получим

что приводится к виду

(6)

Все корни z_i уравнения (1), лежащие внутри единичного круга (рис.1), перейдут в левую полуплоскость w (рис.2). Поэтому при использовании преобразованного характеристического уравнения (6) для устойчивости импульсной системы необходимо и достаточно, чтобы все корни w_i (i=1,2,…,m) имели отрицательные вещественные части. Границей устойчивости будет случай попадания какого-либо корня w_i на мнимую ось, когда все остальные w_i лежат слева от нее.

Пример.

Исследуем уравнение

(7)

Произведя замену переменных согласно (5) а именно

получим

(8)

где

Условием устойчивости такой системы будет положительность коэффициентов уравнения (8). Но это условие нельзя применять к исходному уравнению (7). В самом деле, пусть а₀=1, а₁=3, а₂=10.

Тогда b₀=8, b₁=-18, b₂=14. Поскольку не выполнено необходимое условие устойчивости для уравнения (8) – положительность коэффициентов, - то данная система будет неустойчивой, хотя исходное уравнение (7) имеет все положительные коэффициенты.

Вычислим, какие при этом корни будут иметь исходное уравнение (7)

Для устойчивости требуется

Т.е. система с данными коэффициентами характеристического уравнения действительно неустойчива.

Определение устойчивости линейной ДАС по расположению корней характеристического уравнения относительно окружности единичного радиуса связано с трудоемкими вычислениями при высоком порядке уравнения. В связи с этим, все известные в теории САУ непрерывного действия критерии устойчивости были обобщены для исследования дискретных систем. Применение этих критериев позволяет без вычисления корней характеристического уравнения устанавливать соотношения для определения устойчивости, вытекающие из неравенства (2). Рассмотрим критерии, наиболее часто применяемые на практике.

9.3 Критерии устойчивости.

Аналог критерия Михайлова.

Аналог критерия Михайлова позволяет исследовать устойчивость импульсной системы непосредственно по исходному характеристическому уравнению (1), не преобразовывая его.

Вывод такого критерия делается аналогично выводу критерия Михайлова, но в другой комплексной плоскости, следующим образом.

Согласно принципу аргумента число корней многочлена

(9)

лежащих внутри единичного круга можно определить по числу полных оборотов вектора H(z) при изменении z вдоль границы этого круга, т.е. при

Следовательно если все m корней характеристического многочлена (9) лежат внутри единичного круга, то

,

Это условие необходимое и достаточное для устойчивости импульсной системы.

Поскольку известно свойство

то достаточно рассмотреть интервал и потребовать

(10)

это и является аналогом критерия устойчивости Михайлова для импульсных систем

Подстановка в (9) дает

(11)

причем в крайних точках и имеем

()

По выражению (11) строится аналог кривой Михайлова, причем в этом выражении выделяется вещественная и мнимая части:

Для устойчивости импульсной системы, например, при m=3 аналог кривой Михайлова имеет вид, изображенный на рис.3; для неустойчивой системы при m=3 – вид, изображенный на рис.4. Из этого примера хорошо видна специфика очертания аналога кривой Михайлова для импульсных систем по сравнению с непрерывными.

Очевидна здесь и другая формулировка аналога критерия Михайлова – перемежаемость корней (рис.5).

Y^* Y^*

Y^*

0 0

X^* X^*

X^*

Рис.3 Рис.4 Рис.5