
лекции / В. А. Бородавкин, И. Л. Петрова -ТАУ дискретных систем / 2 Лекция
.doc
2 Лекция
Содержание лекции:
Дискретные системы: импульсные, цифровые, релейные.
Виды модуляции.
Решетчатая функция.
-
Дискретные системы автоматического управления.
Основные понятия. Терминология. Квантование сигналов.
В технике управления наряду с непрерывными широко применяются дискретные системы, в которых контур управления замыкается только на определенные промежутки времени, осуществляя воздействие на исполнительный орган импульсами. В паузах между импульсами цепь управления остается разомкнутой.
Дискретные САУ – это системы, в которых содержится одно или несколько звеньев, производящих квантование непрерывного сигнала в дискретный. Таким образом, процесс преобразования непрерывной величины в дискретную называют квантованием. Различают квантование по уровню и по времени.
При
квантовании по времени значения
непрерывного сигнала выделяются в виде
дискретных сигналов через равные
промежутки времени
![]() ,
при этом уровни сигнала могут принимать
произвольные значения (рис.1).
,
при этом уровни сигнала могут принимать
произвольные значения (рис.1).
При
квантовании по уровню осуществляется
преобразование непрерывного сигнала
в дискретный в произвольные моменты
времени с выделением значений непрерывного
сигнала в момент пересечения им
равноотстоящих уровней
![]() (рис.2).
(рис.2).
При смешанном квантовании происходит преобразование непрерывного сигнала в дискретный через равные временные промежутки, но при этом выделяется ближайший уровень непрерывного сигнала (рис.3).

 х
х







![]() 3
3![]() 5
5![]() t рис.1
t рис.1
х



![]()
 0 t
0 t
 -
-![]() рис.2
рис.2
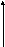





 х
х
 3
3![]()

![]()
 0
0
![]() 3
3![]() 5
5![]() t рис.3
t рис.3
В зависимости от вида квантования различают системы:
-
релейные;
-
импульсные;
-
цифровые.
В релейных системах – квантование по уровню.
В импульсных – по времени.
В цифровых – по времени и по уровню.
При большой разрядной сетке цифровых систем (малый шаг квантования по уровню) квантованием по уровню можно пренебречь.
Все релейные системы являются существенно нелинейными.
Импульсные системы (содержащие импульсный элемент) можно рассматривать как линейные.
Импульсный
элемент –
устройство, осуществляющее квантование
сигнала по времени. Выходной сигнал
импульсного элемента представляет
собой последовательность импульсов.
Например, при прямоугольной форме
импульса его можно охарактеризовать
следующими основными параметрами
(рис.4): высотой, или амплитудой, импульса
А;
длительностью, или шириной импульса
![]() ;
периодом повторения импульсов Т;
паузой между соседними импульсами Т-
;
периодом повторения импульсов Т;
паузой между соседними импульсами Т-![]() ;
скважностью
;
скважностью
![]() .
.
Импульсы можно классифицировать по форме: прямоугольные, треугольные, синусоидальные и т.д.
Рассмотрим прямоугольный импульс.
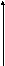
 s
s


![]()

 t
t
![]()

![]() -
период квантования
-
период квантования
![]() -
скважность
-
скважность
![]() -
длительность импульса
-
длительность импульса
Если имеем систему
Им-пульсный Элемент
y(t) ![]()


то
![]()


 функция
формы
функция
формы
Единичный прямоугольный импульс можно представить в виде разложения двух непрерывных функций
![]()
Введем
в рассмотрение идеальный импульсный
элемент, у которого функция формы
импульса есть дельта-функция
![]() .
.
Расчленим условно импульсный элементна две части:
-
простейший импульсный элемент; ()
-
формирователь импульса (ФИ).
S(t)
ФИ
 g(t) u y
g(t) u y


первый дает решетчатую функцию
![]()
![]() .
.
Второй придает каждому импульсу определенную длительность и форму.
Введение идеального импульсного элемента позволяет построить теорию для исследования класса импульсных систем.
Найдем ПФ формирователя импульса для прямоугольного импульса:
![]()
![]()
![]()
![]() (Если
вводится запаздывание в реальной
области).
(Если
вводится запаздывание в реальной
области).
Процесс
квантования непрерывного сигнала в
импульсных системах может рассматриваться
как процесс импульсной модуляции, под
которой понимают изменение какого-либо
параметра переносчика сообщений по
закону передаваемого сигнала. Устройство,
осуществляющее модуляцию, называется
модулятором.
Обычно он имеет два входа, на один из
которых подается подлежащий модуляции
сигнал
![]() ,
а на другой – так называемый «опорный»,
или «несущий» сигнал
,
а на другой – так называемый «опорный»,
или «несущий» сигнал
![]() ,
играющий роль переносчика информации,
содержащейся в сигнале
,
играющий роль переносчика информации,
содержащейся в сигнале
![]() .
Выходной сигнал модулятора (результат
модуляции)
.
Выходной сигнал модулятора (результат
модуляции)
![]() представляет собой функцию входных
сигналов, вид которой зависит от типа
модулятора.
представляет собой функцию входных
сигналов, вид которой зависит от типа
модулятора.




![]()
![]()


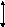


А



0 Т t рис.4

Виды квантования по времени (рис.5).
-
Амплитудно-импульсная модуляция (АИМ) (амплитуда импульса пропорциональна входному сигналу);
-
Широтно-импульсная модуляция (ШИМ) (ширина импульса пропорциональна входному сигналу);
-
Фазо-импульсная модуляция (ФИМ) (фаза импульса пропорциональна входному сигналу).
Во всех случаях период чередования импульсов (период квантования) является постоянным. Возможны и более сложные случаи.
ИЭ
x(t) y(t)


x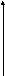





 T
– период
квантования
T
– период
квантования
x(t)
0
t
x
x[nT] - решетчатая
функция



 x[nT]
x[nT]




T nT t

 АИМ
АИМ
y

 Длительность
Длительность
![]()
(0<<1)
![]() Величина
импульса x[nT]
Величина
импульса x[nT]


 x
x ![]()



 t
t
y
ШИМ ![]()



![]()
![]()
![]()


![]()


![]()





![]() t
t
y

![]() ФИМ
ФИМ



![]()

![]()
T nT t
Рис.5
Рассмотрим амплитудно-импульсную модуляцию.
Период следования импульсов – период квантования.
![]() -
дискретное время, которое может быть
размерным и безразмерным
-
дискретное время, которое может быть
размерным и безразмерным
![]() -
целая часть от
-
целая часть от
![]() .
.


 y
y





 t
t
![]() 3
3![]()
Функция
![]() - решетчатая функция (функция в конкретных
точках – узлах).)
- решетчатая функция (функция в конкретных
точках – узлах).)
Решетчатые функции
Математическое описание импульсных САУ усложняется из-за дискретного характера сигнала. Квантованный по времени сигнал может быть представлен выборкой ординат непрерывной функции времени (см. рис.1). Эти ординаты разделены периодом квантования, а внутри периодов все промежуточные значения равны нулю. Поэтому дискретный сигнал удобно описывать функциями дискретной переменной.
Рассмотрим
функцию времени
![]() ,
определенную для всех значений t
и
тождественно равную нулю для
,
определенную для всех значений t
и
тождественно равную нулю для
![]() .
Пусть n
– натуральное
число (n=0,12,3…)
и Т
– период дискретности. Функцией
дискретного аргумента называется
числовая
последовательность x[0],
x[T],
x[2T],…, x[nT], получающаяся
в результате выборки значений функции
.
Пусть n
– натуральное
число (n=0,12,3…)
и Т
– период дискретности. Функцией
дискретного аргумента называется
числовая
последовательность x[0],
x[T],
x[2T],…, x[nT], получающаяся
в результате выборки значений функции
![]() в точках
в точках
![]() ,
n
–
натуральное
число. Для краткости ее называют
решетчатой
функцией и
обозначают x[n].
При заданном
интервале дискретности Т
то по функции
,
n
–
натуральное
число. Для краткости ее называют
решетчатой
функцией и
обозначают x[n].
При заданном
интервале дискретности Т
то по функции
![]() решетчатая функция функция x[n]
определяется
однозначно. Непрерывная функция
решетчатая функция функция x[n]
определяется
однозначно. Непрерывная функция
![]() - огибающая для своей решетчатой функции
x[n].
Но
поскольку через дискретные точки
решетчатой функции можно провести
множество огибающих, то обратного
соответсвия между решетчатой функцией
и «породившей»
ее функцией
- огибающая для своей решетчатой функции
x[n].
Но
поскольку через дискретные точки
решетчатой функции можно провести
множество огибающих, то обратного
соответсвия между решетчатой функцией
и «породившей»
ее функцией
![]() нет:
x[n]
нет:
x[n]
![]() .
.
Если необходимо определять значения функции между точками квантования, то вводят понятие смещенной решетчатой функции.
Смещенной
решетчатой функцией называется
числовая последовательность - x[T],
x[T+T],…,
x[iT+T],…,
x[nT+T],
0
1,
образованная в результате выборкизначений
функций
![]() в точках
в точках
![]() оси времени,
где
- постоянное
число, лежащее в интервале 01.
Сокращенно
x[n,
].
оси времени,
где
- постоянное
число, лежащее в интервале 01.
Сокращенно
x[n,
].
Поскольку значения решетчатой функции известны только для дискретных значений аргумента,то для изучения поведения таких функций методы дифференциального и интегрального исчисления оказываются непригодными. Для оценки свойств решетчатой функции используется аппарат конечных разностей и конечных сумм, позволяющий оценивать свойства числовых последовательностей (функций дискретного аргумента). Для исследования динамики дискретных импульсных СУ используются разностные уравнения. Их решение, так же как и дифференциальных, представляет известные трудности. В связи с этим, в теории дискретных (импульсных) САУ широко используются операционные методы.
Аналог преобразования Лапласа – это дискретное преобразование Лапласа или т.н. Z – преобразование.
Z
– преобразованием
решетчатой функции
![]() называется функция комплексного
аргумента Z,
определяемая выражением
называется функция комплексного
аргумента Z,
определяемая выражением
![]() , (1)
, (1)
Это
выражение может быть получено следующим
образом. Если предыстория системы
относительно
![]() учитывается соответствующими граничными
условиями, то допустимо полагать, что
непрерывная функция времени
учитывается соответствующими граничными
условиями, то допустимо полагать, что
непрерывная функция времени
![]() при t<0.
В этом
случае, как известно, функция
при t<0.
В этом
случае, как известно, функция
![]() может быть заменена изображением по
Лапласу (одностороннее преобразование)
может быть заменена изображением по
Лапласу (одностороннее преобразование)
![]() (2)
(2)
Взяв
конечный интервал времени равным периоду
дискретности (![]() )
и представив текущее время в виде
последовательности
)
и представив текущее время в виде
последовательности
![]() можно в выражении (2) интеграл заменить
суммой, а величину dt
периодом
квантования
можно в выражении (2) интеграл заменить
суммой, а величину dt
периодом
квантования
![]() :
:
![]() . (3)
. (3)
Выражение
(3) представляет собой дискретное
преобразование Лапласа. Предел этого
выражения при
![]() даст преобразование Лапласа непрерывной
величины (2).
даст преобразование Лапласа непрерывной
величины (2).
Если
обозначить
![]() ,
то
,
то
![]() (4)
(4)
(


 Обозначив
Обозначив
![]()
![]() )
)
Комплексное
переменное
При этом Z-преобразование, как следует из формулы (1), отличается от дискретного преобразования Лапласа только множителем Т, т.е.
![]() .
.
Итак,
преобразование Лапласа для дискретной
функции привело к бесконечной сумме.
Бесконечная сумма является функцией
комплексного переменного
![]() .
.
Операция
суммирования носит название прямого
дискретного преобразования Лапласа
(или Z-преобразования)
для решетчатой функции
![]() в функцию комплексного переменного
Z. Эта
операция кратко обозначается как
в функцию комплексного переменного
Z. Эта
операция кратко обозначается как
![]() И
указывает, что
И
указывает, что
![]() есть Z
– изображение
решетчатой функции
есть Z
– изображение
решетчатой функции
![]() или, короче,
или, короче,
![]() .
Соответственно
.
Соответственно
![]() является оригиналом
является оригиналом
![]() .
Изображение
.
Изображение
![]() существует, если (1) сходится.
существует, если (1) сходится.
На основе выражения (1) получены таблицы Z-преобразований различных функций времени.
