
лекции / В. А. Бородавкин, И. Л. Петрова -ТАУ дискретных систем / 4 Лекция
.doc
4 Лекция
Математические модели импульсных систем в виде разностных уравнений и структурных схем.
Математические основы теории импульсных систем.
4.1 Математические основы теории импульсных систем.
Приведем основные положения, рассмотренные на предыдущей лекции.
Запишем основные формулы, применяемые при исследовании
непрерывных САУ:
Преобразование Лапласа
![]()
![]()
![]() ; (1)
; (1)
![]() ;
(прямое)
;
(прямое)
![]() ; (2)
; (2)
![]() .
(обратное)
.
(обратное)
дискретных САУ:
а) Дискретное преобразование Лапласа (D-преобразование)
![]() -
оригинал
(решетчатая функция)
-
оригинал
(решетчатая функция)
![]() -
изображение
-
изображение
![]()
![]() (3)
(3)
q=st=+j - комплексная переменная
![]() -
смещенная
решетчатая функция
-
смещенная
решетчатая функция
![]() (4)
(4)
![]() (5)
(5)
(5) – D-преобразование для смещенной решетчатой функции.
Примечание:
В
зависимости от
![]() ряды (3), (5)
могут быть как сходящимися, так и
расходящимися.
ряды (3), (5)
могут быть как сходящимися, так и
расходящимися.
Теорема:
Ряд 3 сходится
абсолютно в каждой точке переходного
процесса
![]() ,
равномерно в переходном процессе
,
равномерно в переходном процессе
![]() и расходится
в переходном процессе
и расходится
в переходном процессе
![]() .
.
Пример 1.
Дано:
Функция
![]()
Найти:
Определить
D –
преобразование
функции
![]()
Решение:
![]()
Это
геометрическая прогрессия
![]() (r
-
знаменатель)
(r
-
знаменатель)
Сумма
членов геометрической прогрессии со
знаменателем
![]()
![]() ;
;

![]()
б) Z – преобразование. (Принципиальной разницы между D-преобразованием и Z – преобразованием не существует.)
Вводится
новая переменная
![]() ,
,
![]()
![]()
Если
известно изображение
![]() некоторой
решетчатой функции, то соответствующее
изображение
некоторой
решетчатой функции, то соответствующее
изображение
![]() может быть найдено с помощью замены
комплексной переменной q
на q=lnZ.
может быть найдено с помощью замены
комплексной переменной q
на q=lnZ.
![]()
аналогично
![]()
т.о. принципиальной разницы между D-преобразованием и Z – преобразованием не существует.
Непосредственно из определения D-преобразования по формуле
![]() (*)
(*)
следует,
что функция
![]() является
периодической вдоль мнимой оси плоскости
q
c периодом
2.
является
периодической вдоль мнимой оси плоскости
q
c периодом
2.
Действительно
![]() (**)
(**)
где
r
– любое
целое число. Поэтому достаточно получить
свойства функции
![]() в любой полосе шириной 2.
Наиболее
удобна для этой цели полоса
в любой полосе шириной 2.
Наиболее
удобна для этой цели полоса
![]() ,
симметричная
относительно действительной оси
плоскости q.
Она называется основной
полосой (рис.1).
,
симметричная
относительно действительной оси
плоскости q.
Она называется основной
полосой (рис.1).
q z
![]()
![]() e
e










![]() 1
1
1



 Re
Re
Re
Re
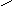

-![]()
Рис.1 Рис.2
Связь между областями определения D-преобразования (в плоскости комплексного переменного q) и Z – преобразования (в плоскости комплексного переменного Z).
Преобразование
![]() переводит основную полосу плоскости q
на всю
расширенную плоскость комплексной
переменной Z.
При этом
отрезок мнимой оси
переводит основную полосу плоскости q
на всю
расширенную плоскость комплексной
переменной Z.
При этом
отрезок мнимой оси
![]() отображается в окружность единичного
радиуса
отображается в окружность единичного
радиуса
![]() (
(![]() ).
Левая полуполоса Re
q<0 плоскости
q
отображается во внутренность единичного
круга /Z/<1
плоскости
Z,
а правая полуполоса Re
q>0 –
во внешность этого круга (рис.2).
).
Левая полуполоса Re
q<0 плоскости
q
отображается во внутренность единичного
круга /Z/<1
плоскости
Z,
а правая полуполоса Re
q>0 –
во внешность этого круга (рис.2).
Связь
между преобразованием Лапласа и
D-преобразованием
осуществляется с помощью
![]() - преобразования.
- преобразования.
![]() - преобразование позволяет определить
изображение
- преобразование позволяет определить
изображение
![]() решетчатой функции
решетчатой функции
![]() по заданному
изображению по Лапласу
по заданному
изображению по Лапласу
![]() функции
функции
![]() .
.
В
ТАУ
![]() -преобразование
позволяет установить связь между
свойствами непрерывных и импульсных
систем.
-преобразование
позволяет установить связь между
свойствами непрерывных и импульсных
систем.
Пусть
![]() (безразмерное время),
(безразмерное время),
![]() ,
,
![]()
Преобразование
Лапласа для функции
![]() запишем в виде
запишем в виде
![]() (
(![]() - безразмерный аргумент)
- безразмерный аргумент)
![]()
где
![]() .
.
Таким образом
![]()
Обозначим
![]() ,
тогда справедливы следующие равенства:
,
тогда справедливы следующие равенства:
![]()
![]() ;
;
![]()
![]()
Это
формулы и обозначения для прямого и
обратного
![]() - преобразования.
- преобразования.
Теоремы для выполнения Z – преобразований (аналогично с непрерывными функциями).
-
Теорема линейности.
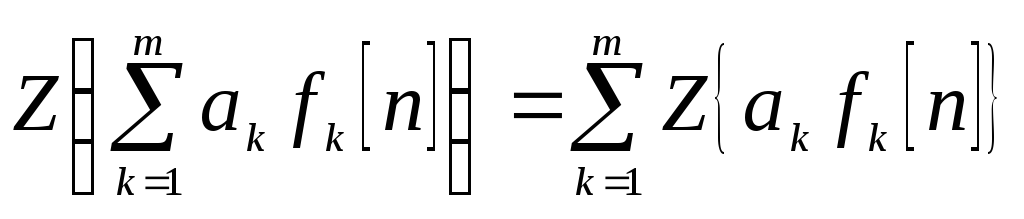
-
Теорема сдвига. (Смещения аргумента в области оригиналов на целое число периодов повторения)
![]()
4.2 Модель импульсной системы в виде структурной схемы.

![]()
![]()


![]()
![]()
![]()
Дискретная передаточная функция – отношение изображений выходной и входной величины при нулевых начальных условиях.
Другой способ определения дискретной передаточной функции изложен ниже. Этапы:
2 ![]()
Аппарат D - и Z – преобразований позволяет использовать частотные методы для анализа импульсных систем.
Примечание:
При
исследовании импульсных систем часто
бывает удобно пользоваться нормированными
выражениями, в которых аргумент
![]() -
безразмерный.
Время
-
безразмерный.
Время
![]() измеряется в долях периода повторения
Т:
измеряется в долях периода повторения
Т: ![]() .
.
При
этом период
становится равным единице, а длительность
импульса – равной скважности. Решетчатая
функция, соответствующая непрерывной
функции
![]() ,
будет
,
будет
![]() ,
а смещенная решетчатая функция -
,
а смещенная решетчатая функция -
![]() .
.
Чтобы
перейти от обычных изображений Лапласа
к нормированным, надо заменить S
на q/T
и разделить
передаточную функцию на Т.
Если
![]() - ненормированное Z
– преобразование,
то нормированное преобразование можно
получить, заменив Т
на единицу.
- ненормированное Z
– преобразование,
то нормированное преобразование можно
получить, заменив Т
на единицу.
По аналогии с определениями теории непрерывных систем функции
![]()
![]()
называются передаточными функциями разомкнутой импульсной системы.
Выражения
ПФ импульсных систем аналогичны
выражениям дробно-рациональных функций
![]() аргумента
аргумента
![]() в изображении решений разностных
уравнений Линейные импульсные системы
с линейной непрерывной частью могут
быть описаны уравнениями в конечных
разностях в дискретные моменты времени
n=0,
1, 2, … .
в изображении решений разностных
уравнений Линейные импульсные системы
с линейной непрерывной частью могут
быть описаны уравнениями в конечных
разностях в дискретные моменты времени
n=0,
1, 2, … .
Основные свойства передаточных функций импульсных систем.
-
ПФ импульсной системы является функцией аргумента
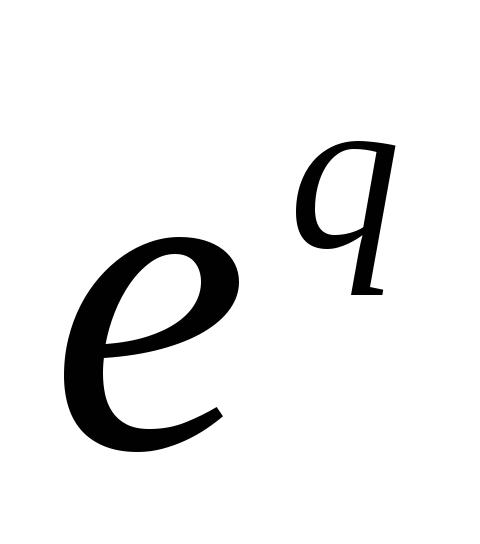 .
Т.к.
.
Т.к.
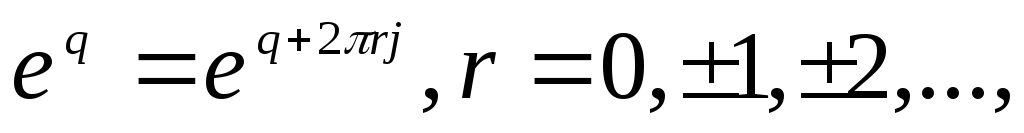 то
то
 есть периодическая функция с периодом
2.
В качестве основной определяющей полосы
обычно выбирают полосу
есть периодическая функция с периодом
2.
В качестве основной определяющей полосы
обычно выбирают полосу
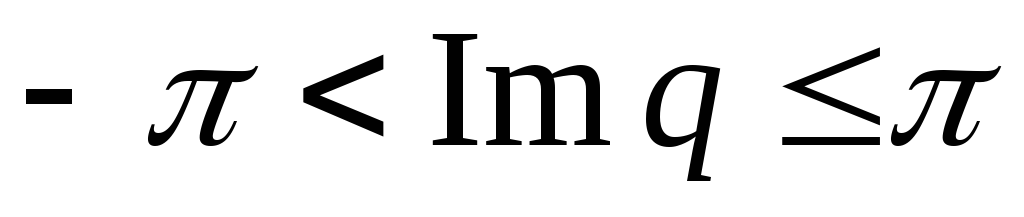 (основная полоса). Все корни полинома
знаменателя, лежащие внутри этой полосы,
называются основными
корнями.
(основная полоса). Все корни полинома
знаменателя, лежащие внутри этой полосы,
называются основными
корнями. -
ПФ
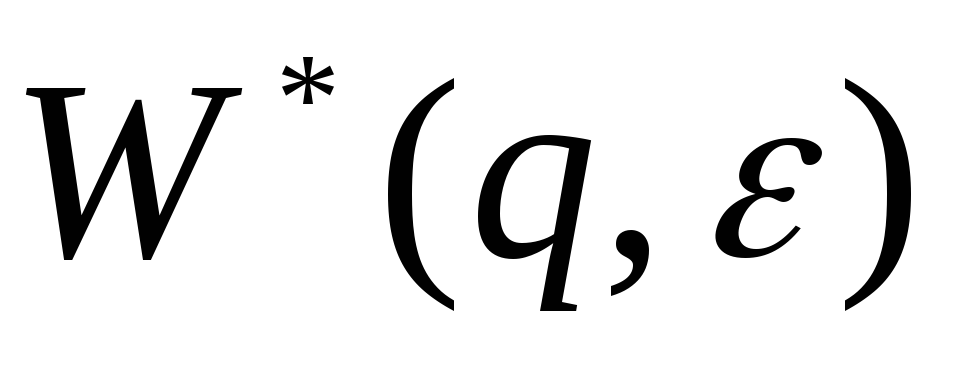 имеет бесчисленное множество значений,
соответствующих различным значениям
параметра
имеет бесчисленное множество значений,
соответствующих различным значениям
параметра
 .
. -
Для импульсов с паузами значения ПФ для интервалов действия отличаются от значений их для пауз.
4.3 Математические модели импульсных систем в виде системы разностных уравнений.
![]()
Рассмотрим дискретное время, заменим производную конечной разностью
 (1)
(1)
запишем (1) в виде рекуррентного соотношения
![]() (2)
(2)
![]() (3)
(3)
![]()
![]() (4)
(4)
Соотношение (3) – разностное уравнение, описывающее импульсную систему.
Запишем Z – преобразование для нулевых начальных условий.
![]()
![]() (5)
(5)
![]() -
передаточная функция
-
передаточная функция
![]()
![]() (6)
(6)
Характеристическое уравнение импульсной системы:
Для
непрерывных ![]()
Для
импульсных ![]()
Для
исследования импульсных систем могут
быть использованы методы теории линейных
непрерывных систем. Для этого необходимо
выполнить конформное отображение
плоскости комплексного переменного Z
на плоскость
комплексного переменного W
т.о., чтобы
единичная окружность
![]() перешла в мнимую ось на плоскости
комплексного переменного W,
а внутренность единичного круга
перешла в мнимую ось на плоскости
комплексного переменного W,
а внутренность единичного круга
![]() отобразилась на левую полуплоскость
Re
W<0
(см.рис.1 предыдущей лекции).
отобразилась на левую полуплоскость
Re
W<0
(см.рис.1 предыдущей лекции).
Такое отображение выполняется с помощью дробно-линейного преобразования
![]()
z W

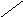 Im
Im
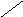
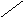
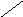







![]() =+- /T
1
0
=+- /T
1
0






![]() =0 Re Re
=0 Re Re



![]()
б) в)
Рис.1
![]()
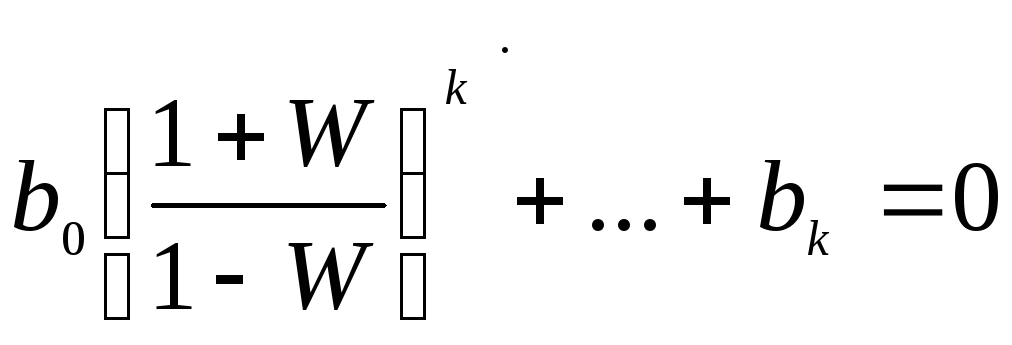
![]()
Например,
![]()
![]()
![]()
![]()
Нули
![]() отображаются в нули
отображаются в нули
![]() по формуле
по формуле
![]() .
.
Отсюда
![]() .
.
Таким образом, можно привести обобщенную структурную схему импульсной системы


 Идеальный
импульсный элемент
Идеальный
импульсный элемент

![]()
![]()


![]()







![]()


![]() -
Приведенная
непрерывная часть.
-
Приведенная
непрерывная часть.
Для такого класса импульсных систем можно построить теорию.
