42. Понятие решетчатой и модулированной функций. Дискретное преобразование Лапласа.

 

Математическим аппаратом для исследования импульсных систем является дискретное преобразование Лапласа.

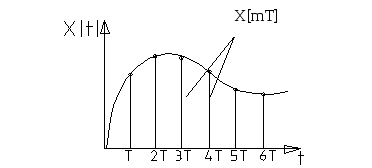
х[mT]-решетчатая функция, состоит из ординат;

 

Модулированный сигнал (последовательность -функций, модулированная ординатами входного сигнала в дискретные моменты времени).

 

;

;

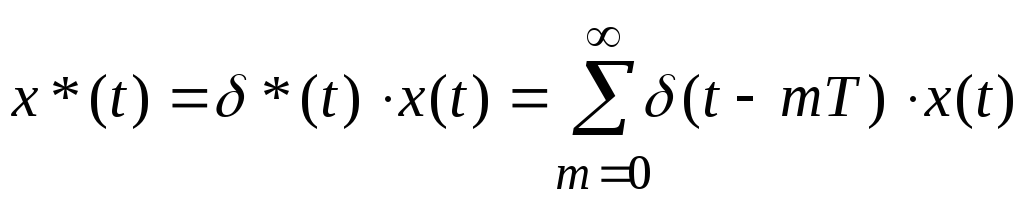Сигнал -реально существующий сигнал;

;

;

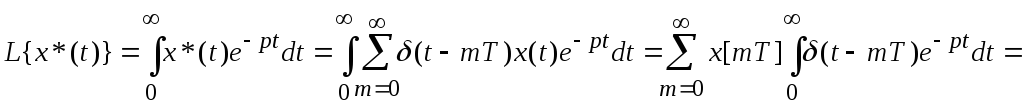
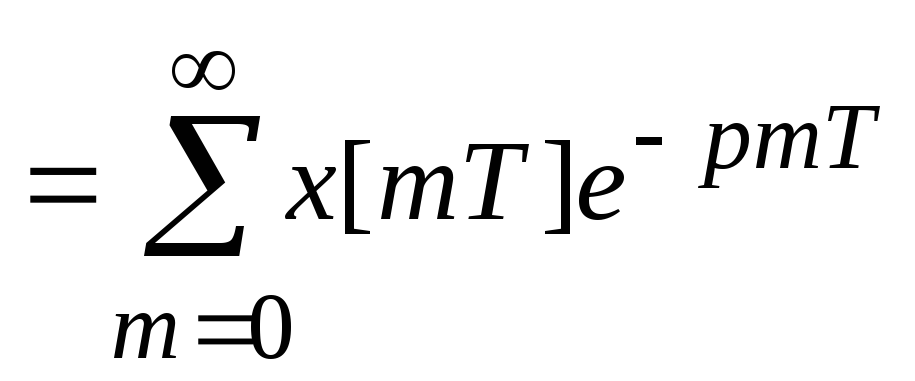D-дискретное преобразование Лапласа.

 

 

43. Свойства дискретного преобразования Лапласа.

1. 1.      Линейность.

;

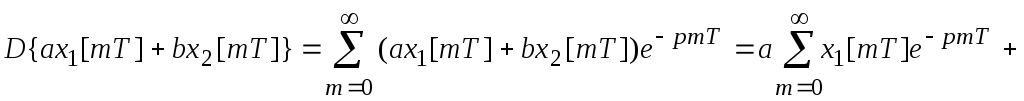
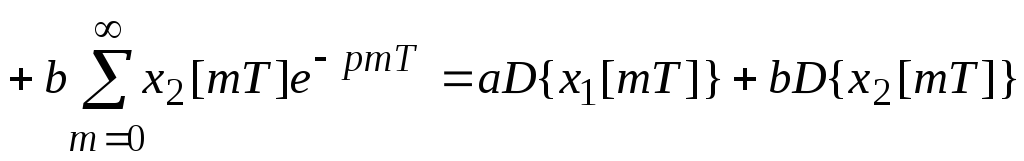2. 2.      (Преобразование Лапласа от запаздывающего аргумента). Смещение по времени.

а) Запаздывание на Sтактов.

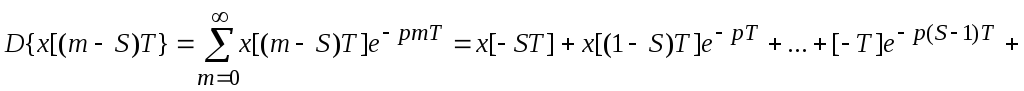
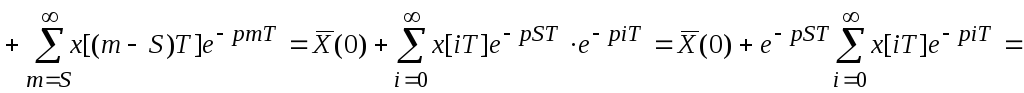
; где i=m-S.

При нулевых начальных условиях (ННУ):

;

;

б) Упреждение m+S=i; m=i-S;

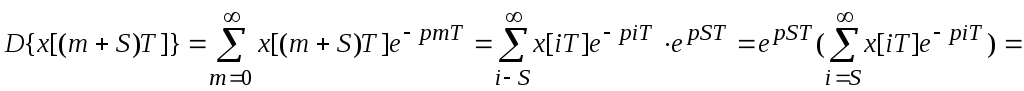
; при не ННУ

При ННУ:

;

;

3. 3.      Преобразование Лапласа от конечных разностей.

Первая разность - ;

;

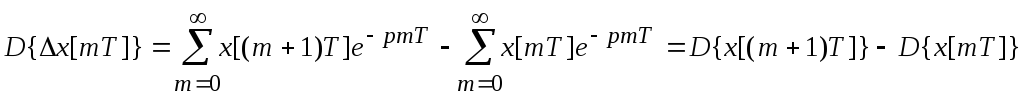При ННУ: ;

Непрерывные системы-p;

Дискретные системы-;

Вторая разность-

;

При ННУ:

;

-к-ая разность-

;

4. 4.      Преобразование от суммы:

Найдем первую разность.

;

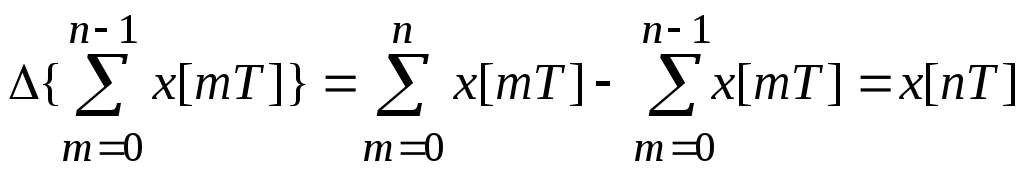Возьмем преобразования Лапласа от правой и левой части выражения.

;

;

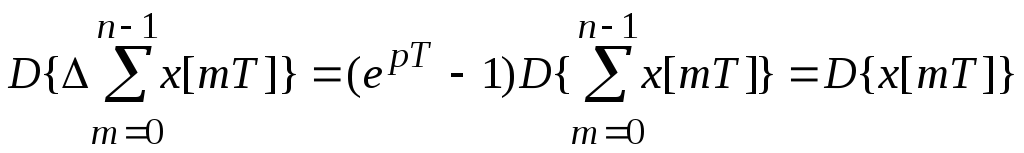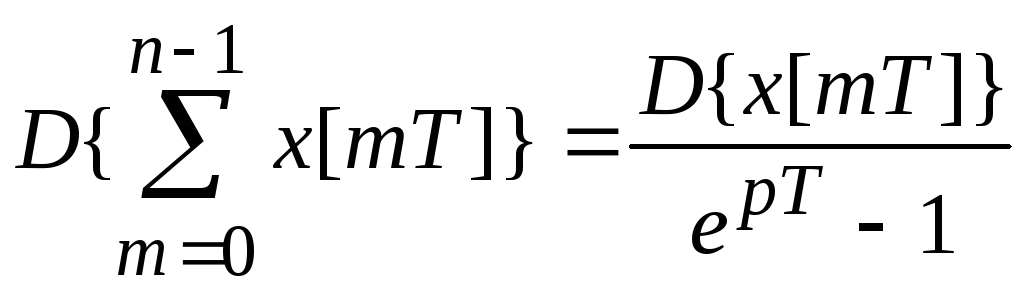5. 5.      Теорема о предельном значении.

По анологии с непрерывными системами:;

6. 6.      Сумма ординат решетчатой функции.

;

;

 

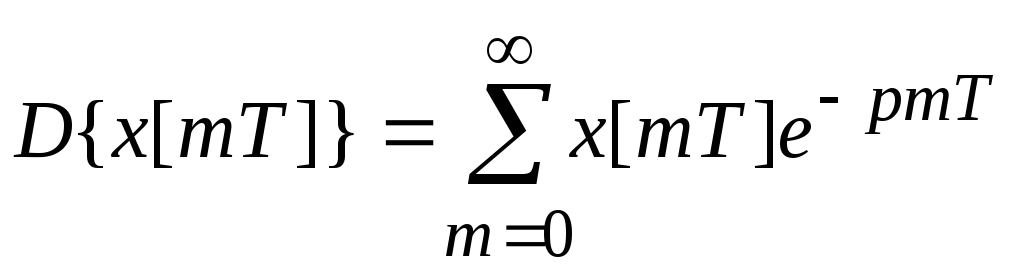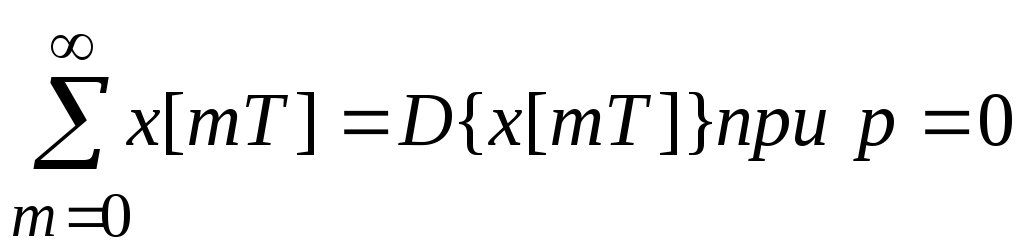44. Дискретные передаточные функции. Дискретные типовые сигналы и их изображение.

Для непрерывных систем: при ННУ;

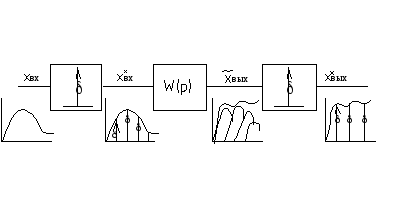Для дискретной системы:

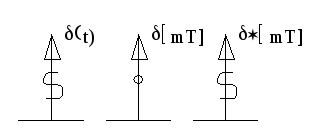
при ННУ;

1. 1.      Дельта-функция.

 

;

;

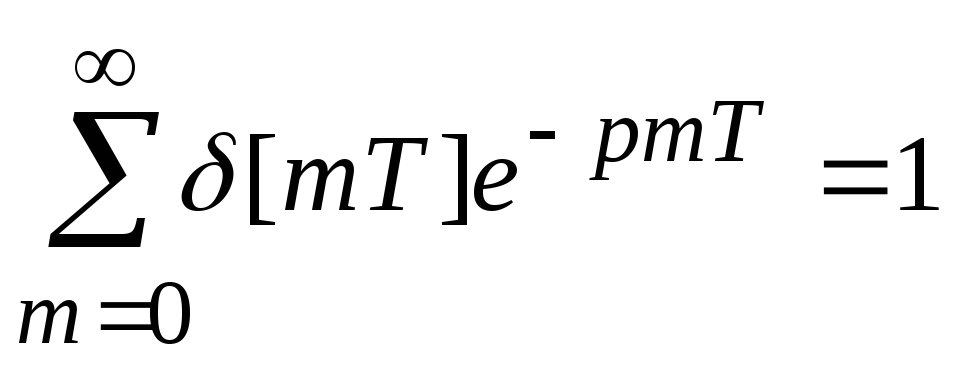2. 2.      Единичная ступенчатая функция.(1(t))

;

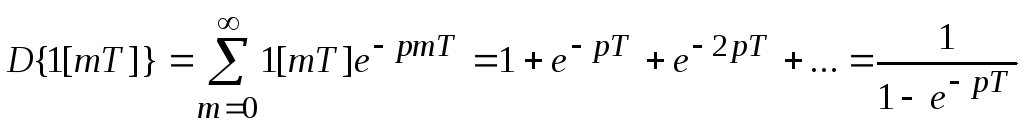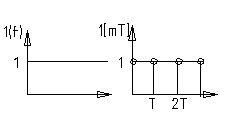Это бесконечно убывающая прогрессия: ;

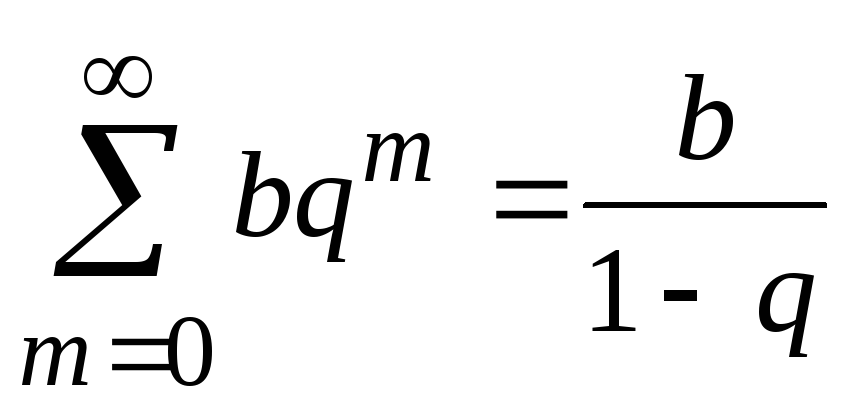3. 3.      Линейно возрастающая функция.

;

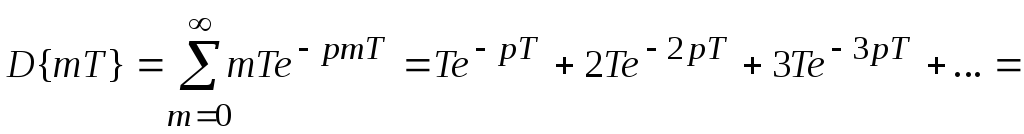
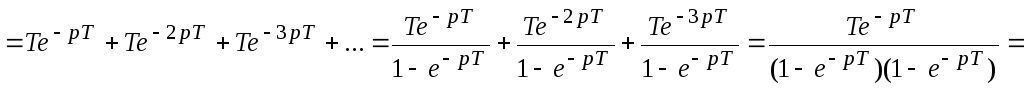
4. 4.      Экспонента.

;

;
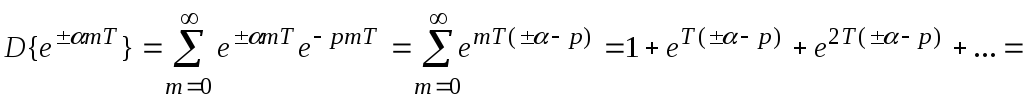