25. Устойчивость систем автоматического управления. Необходимые и достаточные условия устойчивости.

Опр.:Система наз. устойчивой, если после снятия кратковременного воздействия она возвращается в исходное положение.

Опр.:Система наз. нейтрально-устойчивой, если после снятия кратковременного воздействия она занимает новое положение.

Опр.:Система наз. неустойчивой, если после снятия кратковременного воздействия она уходит от положения равновесия.

Применим эти определения к САУ.

1. 1.      Кратковременное воздействие: реакция системы на -функцию является весовая функция .

а) Система устойчива: б) Система нейтральная: в) Система неустойчивая:

 

 

 

 

 

Формула разложения для весовой функции: ,

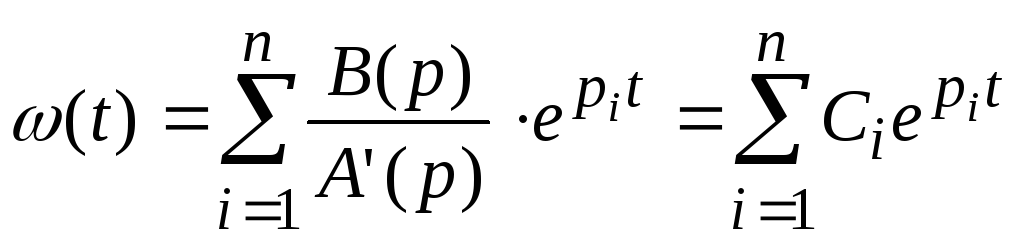где -корни характеристического уравнения А(p)=0;

Как влияет расположение корней на характер весовой функции?

1. Корни :

; ;

; ;

; ;

;

Система устойчива.

2. 2.      Корень , ;

;

Система устойчива.

3. 3.      Корень , , ;

;

Система устойчива.

4. 4.      Корень , ;

;

Система нейтральная.

5. 5.      Корень , ;

Система неустойчива.

6. 6.      Корни , ;

;

Система неустойчива.

Вывод:система устойчива, если все корни её характеристического уравнения лежат в левой части комплексной плоскости. Система нейтрально-устойчивая, если корни её характеристического уравнения лежат в левой части комплексной плоскости и на мнимой оси. Система неустойчива, если хотя бы 1 корень её характеристического уравнения лежит в правой полуплоскости.

Необходимым и достаточным условиемустойчивости линейной системы является расположение её корней (полюсов) в левой части комплексной плоскости.

 

26. Критерий устойчивости Гурвица. Пример.

В основе лежит характеристический полином исследуемой системы.

;

;

По главной диагонали все коэффициенты начиная с а₁.

Выше главной диагонали коэффициенты в порядке возрастания индексов.

Ниже главной диагонали – в порядке убывания индексов.

Формулировка критерия Гурвица:

Для устойчивости системы необходимо и достаточно, чтобы а₀>0, (i=1..n).

Система нейтрально-устойчива, если хотя бы один определитель Гурвица равен нулю.

на границе колебательной устойчивости;

на границе апериодической устойчивости (1 из корней попал в ноль);

Определитель Гурвица , получается отчеркиваниемiстрок иiстолбцов из определителя .

Частный случай устойчивости системы:

, ;

;

Если: , то система устойчива.

 

27. Принцип аргумента. Критерий устойчивости Михайлова.

Принцип аргумента.

Рассмотрим А(р) при подстановке jwвместо р.

А(jw)-характеристический полином от аргументаjw.

;

Если рассматривать А(jw):

;

-это фаза (аргумент);

;

Обычно интересуются приращением:

при ;

при ;

 

Приращение аргумента вектора А(jw) равно разности левых и правых полюсов, умноженной на при изменении частоты от и умноженной на при изменении частоты от .

Критерий Михайловаявляется геометрической интерпретацией принципа аргумента.

Ответим на вопрос: является ли система с характеристическим полиномом А(р) устойчивой?

Пусть в А(р) нет нулевых корней. Частоту изменяем от . Еслиl=0, то правых корней нет, т.е. система устойчива.

Примеры устойчивости гадографов Михайлова.

1. 1.      , , , полагаем, что >0;

2. 2.      , , ;

3. 3.      и т.д.

Для устойчивости системы необходимо и достаточно, чтобы гадограф Михайлова, начинаясь на действительной оси обходил в положительном направленииn-квадрантов.

Гадограф Михайлова-это геометрическое место конца вектора А(jw).(положительное направление-против часовой стрелки).

Примеры неустойчивости:

 

28. Критерий устойчивости Найквиста для устойчивой в разомкнутом состянии системы.

Критерий Найквиста позволяет судить об устойчивости замкнутой системы по гадографу разомкнутой системы. Удобство использования определяется тем, что гадограф может быть построен экспериментально.

Критерий Найквиста связывает разомкнутую и замкнутую систему.

Вводится фунцция: ;

где С(р)-характеристический полином разомкнутой системы, ;

;

При каких условиях замкнутая система устойчива?

При условии устойчивости замкнутой системы изменение в диапазоне от

или будет равно:

, при и при .

Разомкнутая система устойчива.

Характеристический полином разомкнутой системы не имеет правых корней (l=0).

при и при ;

Т. о. , система автоматического регулирования устойчива, если изменение аргумента вектора F(jw) при изменении w от 0 до , равно нулю.

;

На рис.(*) показаны два годографа ; 1-соответствует устойчивой системе: он не охватывает точку (0,0), 2-неустойчивой: он охватывает точку (0,0). Так как отличается от от на +1, то сказанное можно сформулировать непосредственно для характеристики . рис.(**)

 

Формулировка:

Если разомкнутая система устойчива, то для устойчивой замкнутой системы необходимо и достаточно, чтобы гадограф разомкнутой системы не охватывал точку с координатами (-1, j0).