Решение.

где , .

Исключим t из выражений. Подставим в выражение для . , тогда – семейство парабол, направленных в отрицательную сторону оси с вершиной в точке В(;0), причем каждая парабола является образом двух прямых: z = ± C+i. (рис. 28).

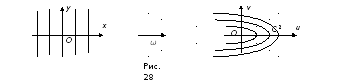
Замечание. Обратная к степенной функция – – многозначная, ее однозначная ветвь, выделяемая образом одной их точек, отображает плоскость (z) с разрезом по неотрицательной оси (Оx) на соответствующий сектор.

5. Показательная функция

Функция является периодической с мнимым периодом . Это гармоническая функция; отображение, осуществляемое ей, конформно на всей плоскости.

Пример . Найти образы семейства прямых, параллельных оси (Оу) z = C+it при отображении .

Решение.

т.е. – параметрическое уравнение окружности с радиусом . Когда точка z проходит прямую на плоскости (z), то точка при обходит бесконечно много раз окружность (рис. 29).

Замечание. Обратная к показательной функция является однозначной на римановой поверхности. Ее главное значение определяет конформное отображение всей плоскости () с разрезом ( на полосу шириной , параллельную действительной оси.

6. Тригонометрические и гиперболические функции

1) .

Функция однолистна в полуполосе и отображает эту полуполосу на плоскость с разрезом Склеивание листов римановой поверхности происходит отдельно по лучу и по отрезку [–1,1].

2) .

Функция сводится к при помощи соотношения: .

3) , .

Функции сводятся к и при помощи соотношений: ; .

7. Функция Жуковского

Функция аналитическая во всей плоскости Гаусса за исключением точек z₁ =1, z₂ = –1, z₃ =0, так как .

Функция конформна в расширенной плоскости, за исключением точек z₁ =1, z₂ = –1, z₃ =0 и осуществляет конформное отображение как внешности, так и внутренности единичного круга плоскости (z) на плоскость с разрезом по отрезку Полная плоскость (z) отображается на двулистную риманову поверхность, склеенную крест-накрест по разрезам

Обратная функция – двузначна, причем каждая ветвь осуществляет отображение плоскости с разрезом по на внутренность или внешность единичного круга в плоскости (z).

Конформное отображение, осуществляемое функцией, было использовано Н.Е.Жуковским для решения задач обтекания крыла самолета.

§ 8. Интеграл от фкп п. 1. Определение, теорема существования

Пусть l – дуга направленной кусочно–гладкой кривой, уравнение которой где , лежащей в плоскости (z). Пусть на l лежат точки А и В. Кривая направлена, значит на ней задано направление: при возрастании t точка перемещается от т. А к т. В. Пусть на кривой задана однозначная и непрерывная ФКП . Разобьем дугу АВ произвольным образом точками на n элементарных дуг, , соответствующим значениям параметра: . Обозначим . Выберем на каждой элементарной дуге по точке , и составим интегральную сумму: .

Определение . Если существует конечный предел интегральной суммы при , который не зависит ни от способа разбиения дуги на элементарные дуги, ни от выбора на них точек , то он называется интегралом от функции по дуге кривой l и обозначается .

Теорема существования. Если функция непрерывна на l , то интеграл от нее по дуге l существует.

(без доказательства)