Решение.
,
,
,
тогда
Пример .
Найти образ окружности
при отображении
.
Решение.
z
= x
+ iy,
= x
– iy.
Подставим в
уравнение окружности
формулы
и
:
,
,
,
.
Заменим
,
.
1)
2)
.
(*)
Заменим
на
Подставим в (*):
1)
– прямая.
2)
(
точка О).
Образом окружности
при отображении
будет прямая
.
Для построения окружности, приведем ее уравнение к каноническому виду:
центр в точке
,
радиус –
(рис. 26).
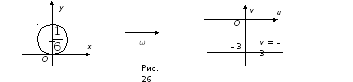
3. Дробно-линейная
функция
,
ad–bc
≠ 0, a,b,c,d
.
может
быть приведена к виду
где
.
–
аналитическая во
всей расширенной плоскости Гаусса,
кроме
.
Если принять, что
,
и углы между кривыми при переходе от
точки
к точке
и наоборот равны, то отображение будет
конформно во всей расширенной плоскости
Гаусса.
Геометрический
смысл отображения:
параллельный перенос, инверсия с полюсом
в точке
,
зеркальное отображение относительно
прямой, проходящей через точку
параллельно действительной оси, и
линейное преобразование. Т.е.
представляется в виде композиции трех
функций: линейной
,
простейшей дробно-линейной
и снова линейной
,
следовательно,
также отображает окружность в окружность.
Замечание 1.
Дробно-линейная функция
вполне определяется заданием образов
трех точек, например, если
,
то
.
( )
Если одна из точек
или
является
бесконечно удаленной, то в формуле все
разности, содержащие эту точку, следует
заменить единицами.
Замечание 2.
Точки А
и В,
симметричные относительно прямой или
окружности в плоскости (z),
отображаются дробно-линейной функцией
в точки Аۥ
и Вۥ,
симметричные относительно образа прямой
или окружности в плоскости
.
Бесконечно удаленная точка считается
симметричной центру окружности.
Замечание 3.
Отображение
,
обратное к дробно-линейному, само
является дробно-линейным, хотя и не
совпадает с прямым отображением, т.е.
не является инволюцией.
Пример . Найти дробно-линейное отображение, переводящее точки 1, i, i–1 в точки 0, 3i, 1+i.
Решение.
Подставим данные
точки в формулу (17):
Преобразуем
полученное выражение.
.
4. Степенная
функция
,
z
≥ 2.
–
аналитическая
функция на всей плоскости Гаусса:
кроме z
= 0. Следовательно, отображение, задаваемое
функцией конформно всюду, кроме начала
координат.
(формула Муавра).
Рассмотрим луч z
= At,
где
выходящий
из начала координат на плоскости (z)
под углом
(
)
к оси (Оx).
Следовательно, образом этого луча на
плоскости (
)
будет луч
,
выходящий из начала координат под углом
к оси
;
.
Если луч z
= At
будет двигаться против часовой стрелки
вокруг т. О
по плоскости (z)
, то луч
будет двигаться с угловой скоростью в
n
раз большей по плоскости (
).
Следовательно, когда луч z
= At
пройдет угловой сектор
,
луч
пройдет всю плоскость (
):
(рис. 27).
Вывод:
сектор раствором
плоскости
(z)
конформно отображается на всю плоскость
(
).
Точки плоскости
(z),
не лежащие внутри сектора, будут
отображаться в точки плоскости (
),
уже занятые отображениями точек
рассматриваемого сектора, но тогда
нарушится взаимная однозначность
отображения. Чтобы такого не происходило,
Риман предложил, что эти точки будут
отображаться на новую плоскость (
,
лежащую над плоскостью (
),
т.е. Риман предложил рассматривать n
– слойную
поверхность для данного отображения:
луч от оси
обходит первый слой поверхности,
переходит на второй и т.д., а пройдя все
n
слоев, переходит на первый. (Это можно
рассмотреть лишь в абстракции).
Определение .
Функцию, осуществляющую такое отображение,
называют многозначной, а n
– слойную
поверхность – римановой. Примеры
многозначных функций:
Ln
.
Определение .
Однозначная
функция
,
аналитическая в области
,
называется однозначной ветвью многозначной
функции
,
если для любой точки
значения
,
принадлежат множеству значений
функции
в точке
.
Определение . Точка z комплексной плоскости, обладающая тем свойством, что обход вокруг нее в достаточно малой окрестности влечет за собой переход от одной ветви многозначной функции к другой, называется точкой ветвления рассматриваемой многозначной функции.
В приведенном выше
примере точками, общими для всех слоев,
или точками ветвления римановой
поверхности являются
.
Геометрический
смысл отображения:
лучи, выходящие из начала координат,
отображаются в лучи; окружность с центром
в начале координат О
и радиусом R
отображается в спираль (проекцией
которой на основную плоскость (
)
является окружность радиуса
),
переходящую постепенно из одного листа
поверхности Римана в следующий и из
верхнего вновь переходящую в нижний.
Пример .
Найти образы семейства прямых, параллельных
оси (Оу)
z
= C+it
при отображении
.
С
– постоянная, t
– переменный действительный параметр.