Теорема Котельникова
Пусть непрерывная функция
преобразуема
по Фурье, примем модель ее спектральной
характеристики
тождественно равной нулю, начиная с
некоторой частоты
:
при
(1)
Тогда функция может быть восстановлена
по своим дискретным значениям
,
отсчитанным с периодом повторения:
(2)
(или с частотой повторения
)
Доказательство:
Рассмотрим уравнение:
Примем
,
тогда получим:
(3)
Если выполняются условия (1) и (2), то из уравнения (3) следует:
при
(4)
Поскольку функция
определяется
преобразованием Фурье непрерывной
функции
,
а
определяется
дискретным преобразованием Фурье
функции
,
последовательно получаем:
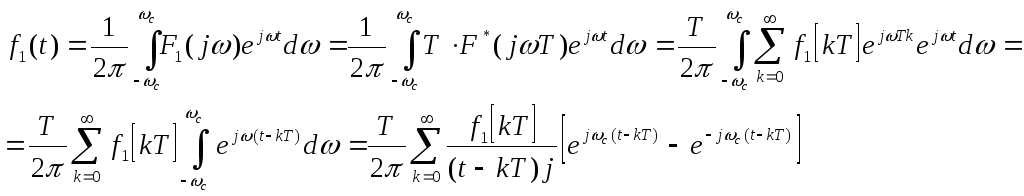Почленное
интегрирование ряда, которое было
использовано при выводе этой формулы,
оправдано тем, что ряд, стоящий под
знаком интеграла, сходится равномерно
при
.
Из последнего равенства следует:
(5)
Эта формула определяет непрерывную
функцию
по
ее дискретным значениям
,
что и доказывает теорему.