
- •I семестр Управление техническими системами.
- •Исторический путь развития автоматики
- •Терминология
- •Объекты управления
- •Обобщенная структурная схема сау
- •Типовая структурная схема 3-х-координатной сау
- •Скорректированная структурная схема регулирования одной величины
- •Классификация сау
- •Фундаментальные принципы управления
- •1. В рассматриваемом случае уравнение системы регулирования будет иметь вид .
- •Статические характеристики звеньев и объектов сау.
- •Динамические характеристики систем регулирования.
- •Типовые входные воздействия
- •Линейные непрерывного действия системы автоматического регулирования
- •Математическое описание сау
- •Передаточная функция сау
- •Переходная функция сау
- •Частотные характеристики
- •Типовые динамические звенья сау
- •Статические (позиционные) звенья.
- •Логарифмические частотные характеристики колебательного звена
- •II. Интегрирующие звенья.
- •III. Дифференцирующие звенья.
- •2. Форсирующее звено.
- •IV. Трансцендентные звенья.
- •Передаточные функции и частотные характеристики систем различной структуры
Логарифмические частотные характеристики колебательного звена
Частотная
передаточная функция колебательного
звена имеет вид
 откуда
откуда
 при
при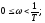

 ;
при
;
при .
.
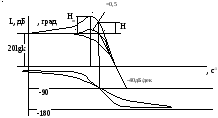
Логарифмическая амплитудно-частотная функция имеет вид

 низкочастотная
асимптота имеет наклон 0 дБ/дек;
низкочастотная
асимптота имеет наклон 0 дБ/дек; высокочастотная
асимптота имеет наклон –
40дБ/дек.
высокочастотная
асимптота имеет наклон –
40дБ/дек. обе
асимптоты пересекаются на сопрягающей
частоте.
обе
асимптоты пересекаются на сопрягающей
частоте.

![]()
![]()

При
значениях 0,5 1 характеристика близка
к ломаной. Если же 0,5, то получается
заметный “горб”. Здесь необходимо
вычислять превышение
 на частоте
на частоте В упрощенных расчетах достаточно
находить
В упрощенных расчетах достаточно
находить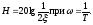
Величина
погрешности на сопрягающей частоте для
различных :

при =1 L=6,
=0,5 L=0,
=0,1 L=-14.
Если от 1 до 0.3, то можно не строить точную ЛАЧХ, а доверитmся асимптотической.
Примеры колебательных звеньев: двигатели постоянного тока, LRC-цепи, регуляторы Уатта и др.
II. Интегрирующие звенья.
Идеальное интегрирующее звено.
Дифференциальное
уравнение
 переходная функция
переходная функция передаточная функция
передаточная функция
![]()


![]()

![]()
![]()
![]()

Дифференциальное
уравнение может быть получено и в такой
форме:
 проинтегрируем это уравнение и получим:
проинтегрируем это уравнение и получим:
Выведем
передаточную функцию:

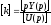 -
размерность передаточного коэффициента;
в частном случае, когда входное воздействие
и выходная функция имеют одинаковую
размерность, [k]=c-1.
-
размерность передаточного коэффициента;
в частном случае, когда входное воздействие
и выходная функция имеют одинаковую
размерность, [k]=c-1.




![]()
Импульсная переходная характеристика:

Пример. Двигатель постоянного тока, выходная координата которого - угол поворота ротора . Постоянную времени двигателя принять малой и не учитывать.


 после
интегрирования получим
после
интегрирования получим
 в форме изображений Лапласа
в форме изображений Лапласа
III. Дифференцирующие звенья.
Идеальное дифференцирующее звено.
Дифференциальное
уравнение
 определим передаточную функцию
определим передаточную функцию






![]()

![]()
Дифференциальное
уравнение записывают и в такой форме:

Пример. Тахогенератор- генератор постоянного или переменного тока, предназначенный для измерения скорости вращения механизмов.


Стат. характ. ТГ Стат. характ. ТГ
пост. тока. перем. тока.
Тахогенератором пост. тока свойственны пульсации из-за коллектора.
Высокий уровень помех и у тахогенераторов переменного тока.
Если пренебречь инерционностью тахогенератора, то, считая входом угол поворота вала, выходом напряжение, тахогенератор можно считать идеальным дифференцирующим звеном.
Пусть измерительным устройством (датчиком скорости) в проектируемой системе является тахогенератор постоянного тока (рис.1.)

При
использовании ТГ в качестве датчика
угловой скорости
 в качестве преобразователя угла поворота
в качестве преобразователя угла поворота

Рис. 1.
-
конденсатор; если uc
– вход,
ic
– выход,
то
 конденсатор – идеальное дифференцирующее
звено.
конденсатор – идеальное дифференцирующее
звено.
2. Форсирующее звено.
Дифференциальное
уравнение
 переходная функция
переходная функция передаточная функция
передаточная функция
ЛЧХ
=1/T
()
L ()
+20
+90
20lgk
, с-1
, град
L, дБ







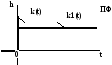

![]()
+45

Пример. ПД-регудятор.

![]()

IV. Трансцендентные звенья.
Звено чистого запаздывания.
(транспортного)

- скорость перемещения ленты;
Q1 – подается через шибер, может меняться (вход);
Q2 – выход.
Время
чистого запаздывания
 .
.
В природе нет ни одного процесса без чистого запаздывания.


 преобразуем
по Лапласу это выражение (теорема
запаздывания), получим
преобразуем
по Лапласу это выражение (теорема
запаздывания), получим
 отсюда
отсюда







Рассмотренные выше наиболее часто встречающиеся на практике основные типы звеньев характеризуются отсутствием корней с положительной вещественной частью характеристических уравнений числителя (т.е. нулей передаточных функций) и знаменателя (т.е. полюсов) называются МИНИМАЛЬНО-ФАЗОВЫМИ. Из всех возможных звеньев с одинаковыми амплитудными характеристиками минимально-фазовые звенья обладают наименьшими по абсолютным значениям фазовыми характеристиками; второе их важное свойство – однозначное соответствие амплитудной и фазовой частотных характеристик (т.е. по амплитудной характеристике можно определить фазовую и наоборот (при k=1) для приведенных амплитудных характеристик).
 -
неминимально-фазовое звено.
-
неминимально-фазовое звено.
В примерах рассматривались звенья, в которых переносчиком информации является постоянный ток. Иногда САУ строятся из звеньев с модулированным сигналом (на несущей переменного тока).
