
ТЕСТ
ПО «ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»
для специальности «Управление и
информатика в технических системах»
дневной формы обучения5 Вариантов по 15 вопросов
Указание: все задания имеют 4 варианта ответа, из которых правильный только один. Номер выбранного ответа обведите кружочком в бланке для ответов.
Вариант 1.
Критерий устойчивости Гурвица.
1) Условие устойчивости по Гурвицу сводится к тому, чтобы при a0>0 все диагональные миноры главного определителя были >0.
2) Если корни характеристического уравнения расположены на комплексной плоскости, то для устойчивости системы необходимо, чтобы все корни лежали слева от мнимой оси.
3) Если характеристическое уравнение линеаризованной системы имеет хотя бы один корень с положительной вещественной частью, то исходная система неустойчива.
4) Чтобы САУ описываемая линейными дифференциальными уравнениями с постоянными коэффициентами была устойчивой, необходимо и достаточно, чтобы вещественные корни дифференциального уравнения были отрицательны.
Передаточная функция апериодического звена 1-го порядка.
А)
![]() В)
В)![]() С)
С)![]() Д)
Д)![]()
Передаточная функция последовательного соединения звеньев.
1)
![]() 2)
2)![]()
3)
![]() 4)
4)
![]()
Понятие времени регулирования системы.
1)
Время регулирования
![]() – это время, в течении которого начиная
с момента приложения воздействия на
систему отклонение регулируемой величины
– это время, в течении которого начиная
с момента приложения воздействия на
систему отклонение регулируемой величины![]() от
ее установившегося значения
от
ее установившегося значения![]() будут
больше наперед заданного значения
будут
больше наперед заданного значения![]() .
.
2)
Время регулирования
![]() – время, за которое регулируемая величина
впервые достигает установившегося
значения.
– время, за которое регулируемая величина
впервые достигает установившегося
значения.
3) Время регулирования определяет быстродействие переходного процесса.
4)
Время регулирования
![]() – это время, в течении которого начиная
с момента приложения воздействия на
систему отклонение регулируемой величины
– это время, в течении которого начиная
с момента приложения воздействия на
систему отклонение регулируемой величины![]() от
ее установившегося значения
от
ее установившегося значения![]() будут
меньше наперед заданного значения
будут
меньше наперед заданного значения![]() .
.
Понятие амплитудно-частотной характеристики системы.
1)
2
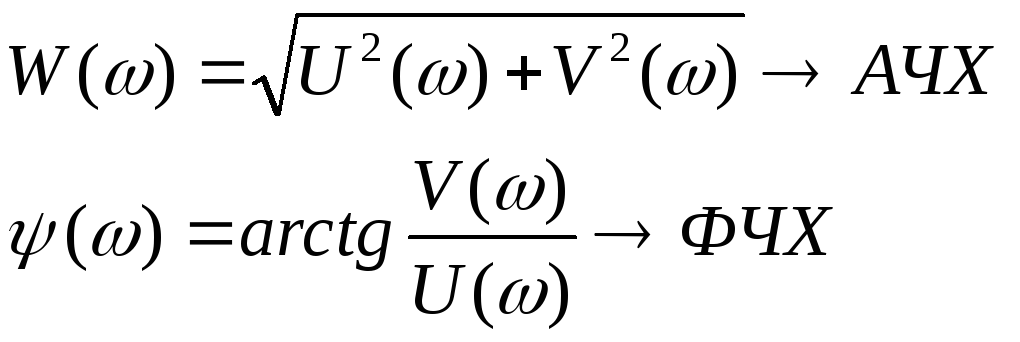
![]()
3)
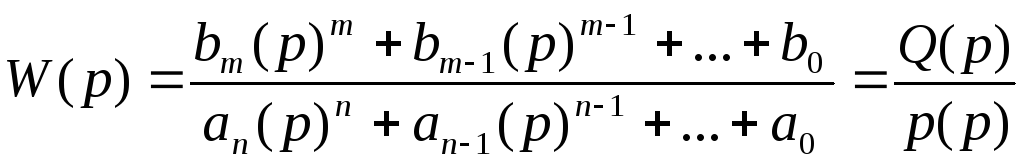 4)
4)![]()
Понятие переходного процесса.
1)
Изображение переходной функции замкнутой
системы при подаче на ее вход ступенчатого
единичного воздействия определяется
выражением:
![]() ,
где переходная функция замкнутой системы
по задающему воздействию.
,
где переходная функция замкнутой системы
по задающему воздействию.
2)
Изображение переходной функции
разомкнутой системы при подаче на ее
вход ступенчатого единичного воздействия
определяется выражением:
![]() ,
где переходная функция замкнутой системы
по задающему воздействию.
,
где переходная функция замкнутой системы
по задающему воздействию.
3)
Изображение переходной функции замкнутой
системы при подаче на ее вход воздействия
определяется выражением:
![]() ,
где переходная функция замкнутой системы
по задающему воздействию.
,
где переходная функция замкнутой системы
по задающему воздействию.
4)
Изображение переходной функции
разомкнутой системы при подаче на ее
вход воздействия определяется выражением:
![]() ,
где переходная функция замкнутой системы
по задающему воздействию.
,
где переходная функция замкнутой системы
по задающему воздействию.
Прямые оценки качества переходных процессов.
1)
1) Время регулирования
![]() .
.
2)
Перерегулирование
![]() .
.
3) Время достижения максимального значения.
4) Резонансная частота.
5) Частота среза.
6)
Полоса пропускания
![]() .
.
2)
![]() - интегральная оценка нулевого порядка;
- интегральная оценка нулевого порядка;
![]() -
интегральная оценка первого порядка;
-
интегральная оценка первого порядка;
……………………..
![]() -
интегральная оценка n-го
порядка.
-
интегральная оценка n-го
порядка.
3)
 1) заданное значение перерегулирования
1) заданное значение перерегулирования![]() ;
;
2)
заданное время регулирования
![]() ;
;
3)
заданный коэффициент передачи
![]() ;
;
4)
заданный порядок астатизма
![]() ;
;
5)
максимально допустимое ускорение
![]() управляемой координаты
управляемой координаты![]() .
.
4)
1) Время регулирования
![]() .
.
2)
Перерегулирование
![]() .
.
3) Время достижения максимального значения.
Понятие нелинейной статической характеристики.
1) Нелинейные звенья:
- с гладкой нелинейной характеристикой;
- с кусочно-линейной характеристикой (релейного типа, зононечувствительности, с насыщением);
- описываемые уравнениями, которые содержат произведение переменных или их производные и другие их комбинации;
логические нелинейные звенья.
2) Статические характеристики нелинейных звеньев могут быть однозначными, неоднозначными релейными, сложными неоднозначными в виде поля.


3) Все нелинейные звенья делят на аналитические (аналитические описания нелинейные характеристики) и неаналитические (характеристика, описывается с указанием логических условий).
4) Нелинейные САУ делятся на 2 группы:
1) с сопутствующими нелинейностями, т.е. нелинейности, проектированные как линеаризованные, но из-за наличия насыщения люфта, мертвого хода, сухого трения, являющиеся практически нелинейными.
2) с преднамеренными нелинейностями, т.е. проектируемые по заданию как нелинейные.
С
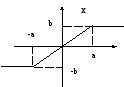 татическая
характеристика нелинейного звена с
насыщением.
татическая
характеристика нелинейного звена с
насыщением.
1)
U
Характеристика описывается выражением:
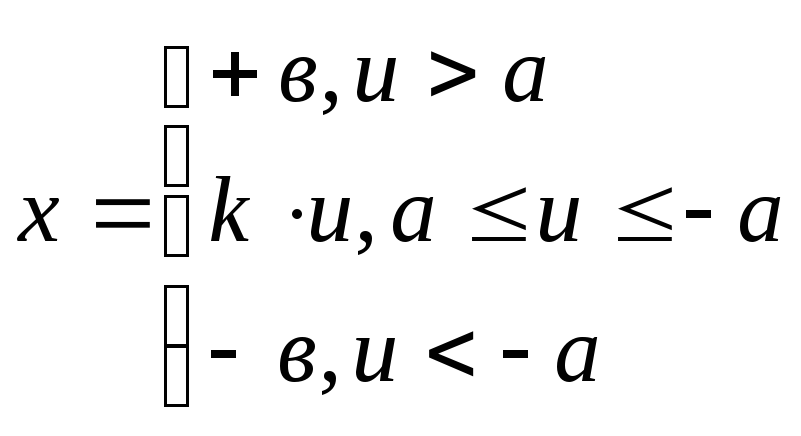
2
x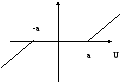 )
)
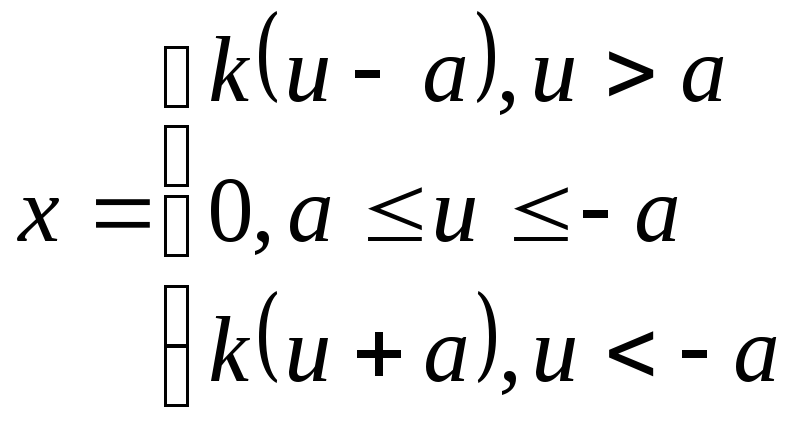
3 )
)
u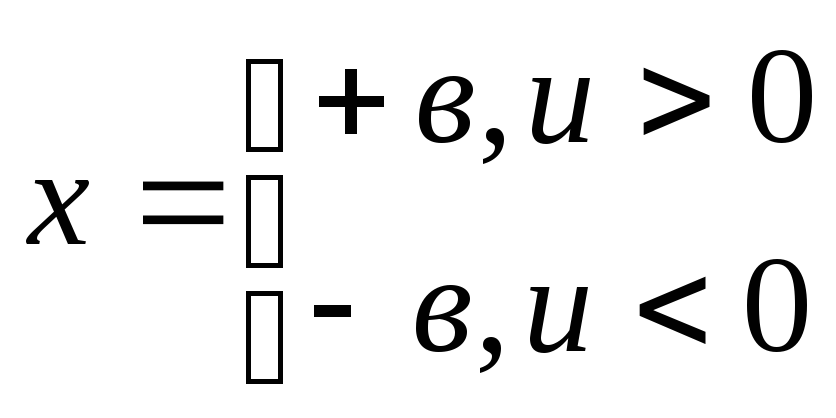
x
4 u b -
b -a a
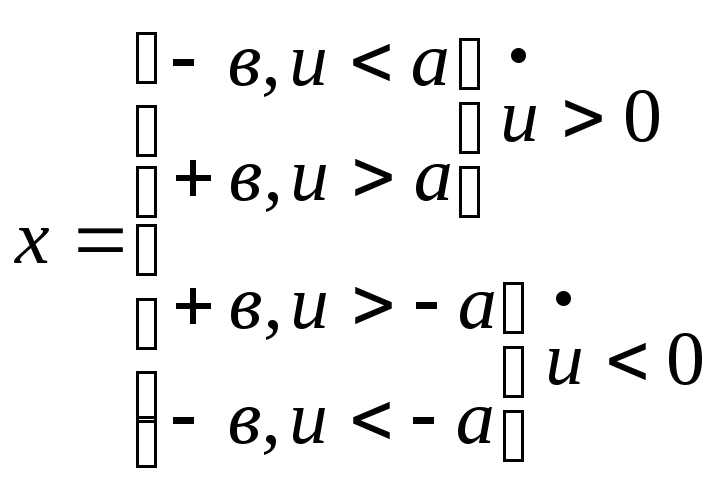
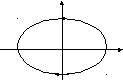
Вид фазовой траектории нелинейной системы.
1
 )
2)
)
2)
4)
3)
Устойчивость нелинейных систем.
1) 1) Если все корни линеаризованного уравнения левые, то исходная нелинейная система устойчива. Эта устойчивость в «малом» в окрестности точки, вблизи которой выполнено разложение в ряд.
2) Если среди корней линеаризованного уравнения есть хотя бы один правый корень, то исходная нелинейная система неустойчива.
3) Если среди корней линеаризованного уравнения есть хотя бы один нулевой корень, то судить о устойчивости нелинейной системы по линеаризованному уравнению нельзя. Для оценки устойчивости необходим анализ влияния старших отброшенных членов разложения в ряд Тейлора.
2)
Поведение СУ, ее устойчивость связана
с отклонением текущих координат
![]() от заданных
от заданных![]() .
.![]() . Если
. Если![]() уменьшается, то система обычно устойчива.
Она считается абсолютно устойчивой,
если выполняется условие
уменьшается, то система обычно устойчива.
Она считается абсолютно устойчивой,
если выполняется условие![]() .
.
3) Система неустойчива в разомкнутом состоянии, число корней, m=2, т.к. годограф Wp(jw) охватывает в положительном направлении точку (-1, j0), один раз, то замкнутая система устойчива.
4)
Система в разомкнутом состоянии
устойчива, тогда изменения аргумента
характеристического уравнения разомкнутой
системы определяется:
![]() .
.
Понятие импульсной системы.
1) Функциональная схема системы с цифровым регулятором
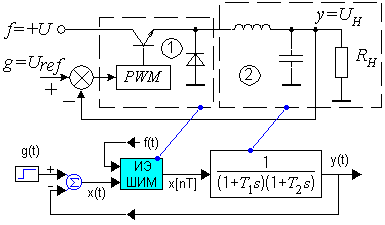
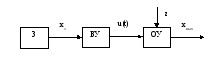
2) Линейной системой импульсного регулирования называется такая САР, которая кроме звеньев описываемых обыкновенными линейными ДУ содержит импульсное звено, преобразующее непрерывное входное воздействие в равноотстоящие друг от друга по времени импульсы.
3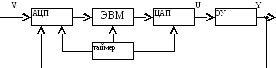 )
)
4)
Выражение для учета дискретного элемента дискретной системы.
1)
![]()
2)
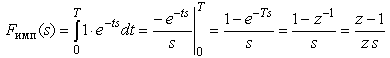
3)
![]() 4)
4)![]()
Устойчивость дискретной системы.
1) Чтобы линейная импульсная система была устойчивой достаточно чтобы модули собственных значений матрицы А были меньше единицы.
![]()
2) Линейная импульсная система устойчива, если все корни лежат в круге единичного радиуса.
3) Линейная импульсная система неустойчива, если все корни лежат в круге единичного радиуса.
4) Чтобы линейная импульсная система была неустойчивой достаточно чтобы модули собственных значений матрицы А были меньше единицы.
![]()
Проведение обратных билинейных преобразований.
А)
Чтобы восстановить непрерывный сигнал
из квантованного с помощью идеального
фильтра (ИФ) с прямоугольной частотной
характеристикой необходимо выполнение
соотношения:
![]() (аналитическая формулировка теоремы
Котельникова-Шеннона).
(аналитическая формулировка теоремы
Котельникова-Шеннона).
В)
Это преобразование позволяет получить
дискретную передаточную функцию
линейного объекта из его исходной
непрерывной передаточной функции:
![]() .
При малом шаге квантования справедлива
следующая замена переменной:
.
При малом шаге квантования справедлива
следующая замена переменной:![]() .
.
С) Используют -преобразование, которое отражает окружность единичного радиуса на мнимую ось комплексной величины , с помощью подстановки:
![]() .
.
Д)
чтобы в системе были процессы минимальной
длительности, все собственные числа
матрицы A
должны быть равны 0,![]() ,
тогда характеристическое уравнение
системы принимает вид:
,
тогда характеристическое уравнение
системы принимает вид:![]()
