5. Структура линейного оператора в конечномерном пространстве.
Теорема
13. Матрица
линейного оператора
в базисе
является диагональной в том и только в
том случае, если все элементы этого
базиса суть собственные векторы оператора
.
(Докажите самостоятельно.)
Если существует
базис пространства
,
целиком состоящий из собственных
векторов оператора
,
то
называют оператором простой структуры.
Покажем на примере, что существуют
операторы, которые не имеют базисов,
состоящих только из собственных векторов.
Ни в каком базисе матрицы таких операторов
не являются диагональными.
Пример.
Пусть
,
– базис пространства
,
и оператор
имеет матрицу
в этом базисе. Предположим, что в другом
базисе
оператор
имеет матрицу
.
Матрицы
и
подобны: существует такая невырожденная
-матрица
,
что
.
Поэтому
.
Это значит, что столбцы матрицы
состоят из координат собственных
векторов оператора
в базисе
.
Найдем собственные значения и собственные
векторы оператора
.
Из уравнения
получаем собственное значение
алгебраической кратности 2.
Координаты собственных векторов
в базисе
найдем из системы уравнений
:
Отсюда
– произвольное число,
,
.
Итак, все собственные векторы коллинеарны
вектору
.
Но тогда матрица
вырождена, – противоречие.
Через
обозначим
-матрицы
вида
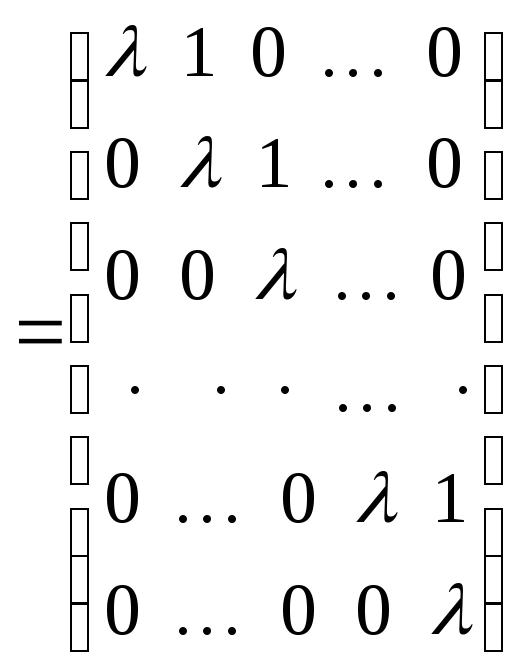
(все элементы главной диагонали
равны
,
стоящие над ними элементы равны 1,
а все остальные – нули);
.
Такие матрицы называют клетками Жордана.
Теорема
14. (Жорданова каноническая форма
матрицы линейного оператора.) Пусть
– конечномерное комплексное
пространство,
.
Пусть
– матрица оператора
в некотором базисе
.
Тогда существует такая невырожденная
матрица
,
что
, (12)
где
,
а
– собственные значения оператора
(не обязательно различные).
(Без доказательства. Доказательство см. в [3, 4, 5].)
Теорема 14
означает, что для любого оператора
,
,
существует базис
,
в котором матрица оператора
имеет квазидиагональный вид (12):
.
При этом каждая жорданова клетка
описывает действие оператора
в некотором его инвариантном подпространстве
,
.
Этот базис
имеет вид
. (13)
В (13) верхний индекс является
порядковым номером жордановой клетки
из (12). Пространство
разложено в прямую сумму
инвариантных относительно
подпространств:
.
Тем самым действие оператора
разбито на действия
индуцированных операторов
.
В каждом подпространстве
,
,
действие оператора
описывается матрицей
–
-ой
по счету жордановой клеткой – в базисе
этого подпространства. Действие
в
состоит в следующем:
(см. определение матрицы линейного оператора в теме 6).
Вектор
является собственным вектором оператора
,
отвечающим собственному числу
;
векторы
называются присоединенными. В
подпространстве
имеется ровно одно одномерное собственное
подпространство
.
Всего у оператора
имеется
собственных векторов
,
которые отвечают собственным числам
;
эти собственные числа не обязательно
различны.
Жорданова форма матрицы линейного оператора определена однозначно с точностью до порядка расположения клеток Жордана. Для операторов простой структуры, и только для них, жорданова форма является диагональной формой матрицы таких операторов.
Для операторов, действующих в действительном пространстве, теорема 14, вообще говоря, не имеет места, так как у таких операторов может не оказаться собственных векторов. Если характеристический многочлен оператора в действительном пространстве имеет только действительные корни, то описание его действия полностью совпадает со случаем оператора в комплексном пространстве. В общем же случае матрицу такого оператора можно привести к виду, в каком-то смысле похожему на каноническую форму Жордана. Однако, легче построить расширение этого оператора на комплексное пространство; идея такого расширения содержится в доказательстве теоремы 9 (см. по этому поводу [4]).