Тема 7. Собственные числа и собственные векторы линейного оператора. Характеристический многочлен.

1. Собственные числа и собственные векторы.

В данной теме будем рассматривать операторы , где – комплексное или действительное конечномерное линейное пространство (или ). Чтобы полностью описать действие оператора в пространстве , надо выбрать базис этого пространства и построить матрицу оператора в этом базисе. Но для некоторых элементов действие оператора на сводится к умножению на некоторое число (если такие существуют).

Определение. Отличный от нуля вектор , , называется собственным вектором оператора , если существует такое число , что . Указанное число называется собственным числом (или собственным значением) оператора , соответствующим собственному вектору .

Множество всех собственных значений оператора называют его спектром. Знание спектра оператора и всех его собственных векторов существенно упрощает описание действия этого оператора и изучение его свойств.

Примеры.

1. . Это линейное пространство отождествим с плоскостью и введем на ней аффинную систему координат заданием базиса . Пусть действие линейного оператора на произвольный вектор состоит в проектировании на параллельно : 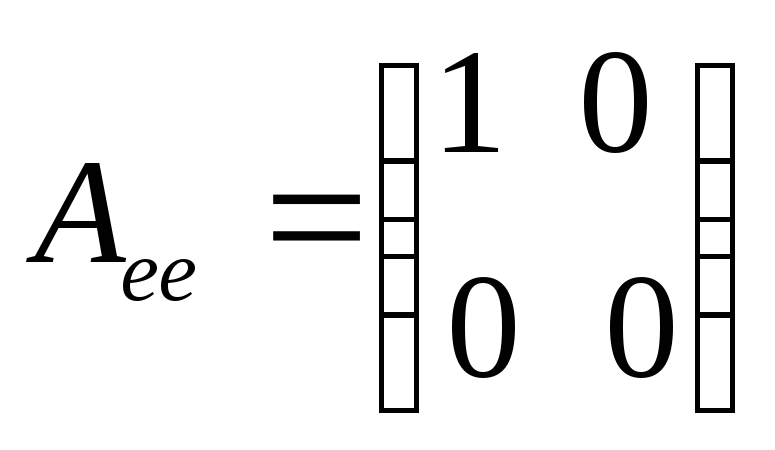. Очевидно, . Число 1 является собственным значением оператора ; все векторы , , являются его собственными векторами, отвечающими этому собственному значению. Кроме того, . Число является собственным значением ; все векторы , , являются собственными векторами, отвечающими .

2. Действие линейного оператора на плоскости состоит в повороте каждого вектора на угол против часовой стрелки с центром поворота в начале координат. Если , то у оператора нет собственных векторов. Если , то любой вектор является собственным, отвечающим собственному числу . Если , то – тождественный оператор, любой вектор является собственным, отвечающим .

3. Для действующего в нулевого оператора любой вектор является собственным, отвечающим .

4. – пространство многочленов степени не выше . – оператор дифференцирования: для любого . Только отличные от тождественного нуля многочлены нулевой степени являются собственными векторами оператора ; они отвечают собственному числу .

Отметим, что если – собственный вектор оператора , то и вектор , где число , является собственным вектором оператора . Поэтому имеет смысл искать только линейно независимые собственные векторы.

Теорема 1. Собственные векторы линейного оператора , отвечающие различным собственным числам , линейно независимы.

Доказательство проведем индукцией по числу . При утверждение теоремы очевидно: один ненулевой вектор по определению образует линейно независимую систему элементов. Пусть утверждение теоремы верно при , т.е. система линейно независима. Докажем, что тогда и векторы линейно независимы. Пусть некоторая их линейная комбинация равна нулю:

. (1)

Подействуем на равенство (1) оператором :

. (2)

Умножим равенство (1) на и вычтем из (2):

.

В силу предположения индукции векторы линейно независимы, поэтому

. Отсюда следует, что все , , так как по условию теоремы при .Тогда из (1) получаем . Но – собственный вектор оператора ; по определению . Поэтому . Итак, равенство (1) возможно только при всех , .

Следствие. Линейный оператор, действующий в -мерном пространстве, не может иметь более различных собственных значений.

Теорема 2. Любое собственное значение оператора не превосходит по абсолютной величине любую его согласованную норму.

Доказательство. Пусть , . Тогда , а в силу согласованности нормы оператора с нормой имеем неравенство . Поскольку , получаем .