3. Характеристический многочлен.
Каждому линейному
оператору мы сейчас поставим в соответствие
некоторый многочлен
,
множество всех корней которого будет
совпадать со спектром этого оператора.
Тем самым задача отыскания собственных
значений оператора будет сведена к
задаче нахождения корней многочлена.
Этого факта для наших целей будет
достаточно; мы не будем здесь изучать
методы нахождения корней многочлена.
Пусть
– линейное пространство над полем
,
,
.
Фиксируем в
произвольный базис
;
оператор
имеет а этом базисе матрицу
.
Сначала введем понятие характеристического
многочлена квадратной матрицы
.
Определение.
Характеристическим многочленом матрицы
называется функция
независимой переменной
.
( Здесь
– единичная
-матрица.)
Теорема
5. Характеристический многочлен
матрицы
является многочленом степени
от переменной
.
Доказательство.
.
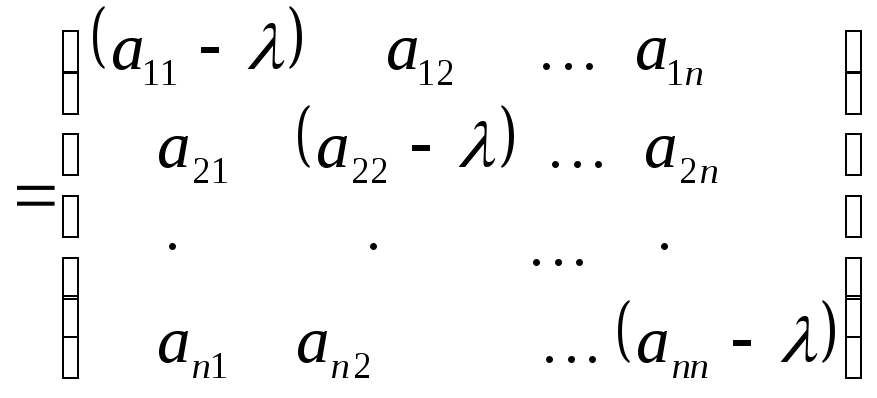Каждый элемент матрицы
представляет собой многочлен от
степени 0 или
1. Поэтому
каждый член определителя
является многочленом от
степени не выше
.
Следовательно, и
тоже является многочленом степени не
выше
.
Докажем, что степень этого многочлена
равна
.
Заметим, что все члены определителя
,
отличные от произведения диагональных
элементов его матрицы
,
суть многочлены степени не выше
.
Поэтому в
слагаемые, содержащие
и
,
определяются только этим произведением
,
которое является многочленом степени
:
очевидно, что старший член этого
многочлена равен
.
Тогда и
– многочлен степени
с тем же старшим членом.
Замечание.
Характеристический многочлен
матрицы
можно записать в виде
.
По теореме Виета для многочлена
(равенство (1*))
– след матрицы
.
Кроме того,
.
Теорема 6. Характеристические многочлены подобных матриц совпадают.
Доказательство.
Пусть
и
.
Тогда
.
Из теоремы 5 темы 6 следует, что две квадратные матрицы одинаковых размеров подобны в том и только в том случае, если они являются матрицами одного и того же линейного оператора. Поэтому получаем
Следствие. Все матрицы одного и того же линейного оператора имеют одинаковые характеристические многочлены. Характеристический многочлен матрицы линейного оператора не зависит от выбранного базиса, а определяется самим оператором.
Характеристическим
многочленом оператора
будем называть функцию
,
,
которая совпадает с характеристическим
многочленом матрицы этого оператора в
произвольном базисе.
Теорема
7. Число
является собственным значением оператора
тогда и только тогда, когда
– корень характеристического многочлена
этого оператора.
Доказательство.
Пусть
– собственный вектор оператора
,
отвечающий собственному значению
:
,
.
Тогда
,
т.е. оператор
вырожденный. Поэтому
,
и
– корень характеристического многочлена.
Обратно: если
– корень характеристического многочлена,
то оператор
вырожденный. А это и означает, что
– собственное значение оператора
.
Теорема 8. Всякий линейный оператор, действующий в конечномерном комплексном линейном пространстве, имеет по крайней мере один собственный вектор.
Доказательство.
Собственные значения оператора
,
и только они, являются корнями его
характеристического многочлена. По
теореме 3 оператор
имеет хотя бы одно собственное значение.
А следовательно, он имеет собственный
вектор.
Замечание.
Если линейный оператор действует в
действительном пространстве, то он
может не иметь собственных векторов. В
самом деле, его характеристический
многочлен – это многочлен с действительными
коэффициентами, который может не иметь
действительных корней. Такая ситуация
возникает, если в (9) присутствуют только
квадратные трехчлены, отвечающие парам
комплексно сопряженных корней многочлена.
Теорема 3 в данном случае не применима:
,
а не
.
Поэтому в случае
возможна ситуация, когда у линейного
оператора нет собственных чисел
.