Тема 1. Матрицы и определители.

1. Матрицы и операции над ними.

Матрица – это прямоугольная таблица чисел. Строки матрицы нумеруют сверху вниз, а столбцы – слева направо. Каждое число такой таблицы записано в строке с некоторым номером и в столбце с некоторым номером ; это число обозначают и называют элементом матрицы, и – индексы этого элемента. Матрица

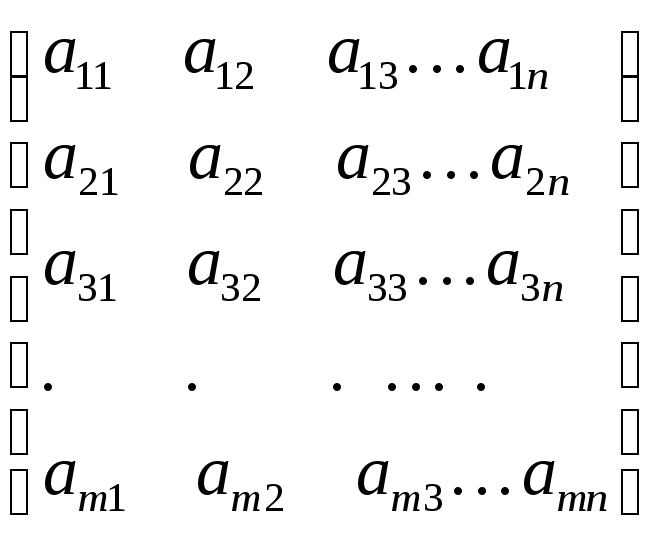
cостоит из строк и столбцов; мы будем обозначать ее короче: . Или еще короче: - матрица , или даже , или вовсе одной большой буквой .

Множество всех действительных чисел принято обозначать буквой , а множество всех комплексных чисел – буквой . Запись означает, что все элементы -матрицы действительны; означает, что элементы матрицы – комплексные числа. Вообще, можно выбрать какое-нибудь множество и построить матрицу из . У нас всегда дальше будет или .

Две матрицы одинаковых размеров иназываются равными, если для всех и всех .

Если матрица состоит из единственной строки, то ее называют матрицей-строкой или вектором-строкой. Матрицу, состоящую из единственного столбца, называют матрицей-столбцом или вектором-столбцом. -ую строку -матрицы с элементами иногда удобно рассматривать отдельно, введя обозначение ; для -го столбца можно ввести обозначение

.

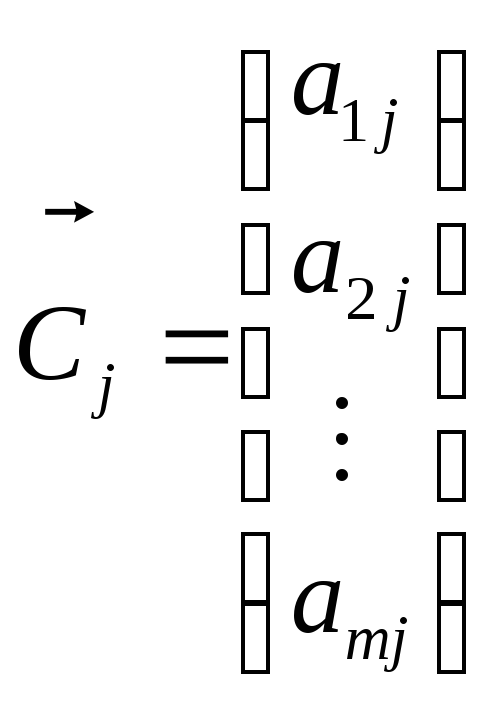Через обозначают множество всевозможных векторов-строк или множество всевозможных векторов-столбцов

с элементами , ( или ). Если потребуется, мы будем указывать, является ли вектором-строкой или вектором-столбцом.

Суммой двух матриц и (одинаковых размеров!) называется матрица с элементами для всех и . Очевидно, что и .

Произведением матрицы на число называется матрица с элементами для всех и . Очевидно, что , , (– числа; – матрицы).

Часто встречается выражение вида . Оно называется линейной комбинацией и с коэффициентами и . Например, если , – векторы-строки, , ,, то их линейная комбинация . Нам придется вводить линейные комбинации .

Пусть – -матрица. Транспонированной матрицей называется -матрица с элементами для всех и . Например, если – вектор-столбец, то – вектор-строка; если – вектор-строка, то .

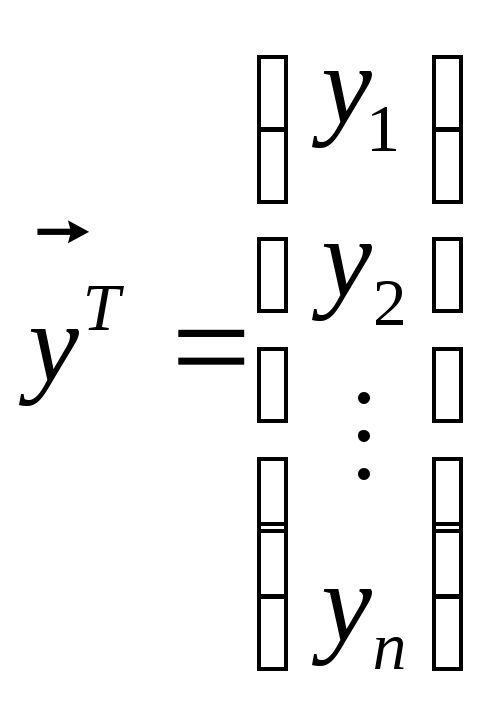Произведением матрицы на матрицу называется матрица с элементами для всех и . Например, если , а вектор-столбец , то вектор-столбец ; если вектор-строка , то вектор-строка .

Задача. Докажите равенства , , .

Если матрицы и прямоугольные (), то имеют смысл произведения и ; оба произведения – квадратные матрицы, но разных размеров: , . Если , то становится разумным вопрос о равенстве матриц и ; в общем случае ответ на него отрицательный.

Примеры матриц и , для которых .

, ; .

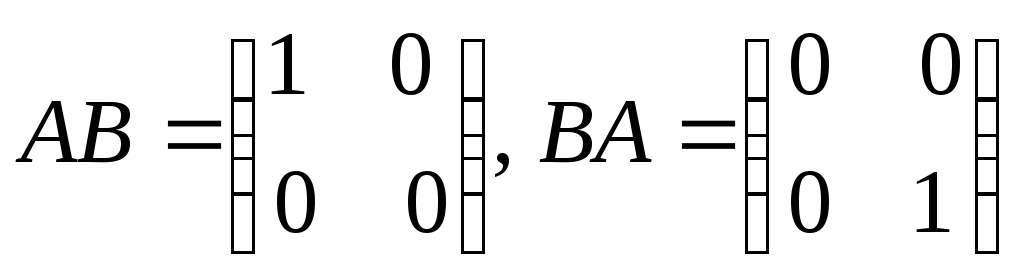Другой пример: , . 

Примеры матриц и , для которых (такие матрицы называются перестановочными).

,; .

Другой пример: .

Матрица, все элементы которой равны нулю, называется нулевой матрицей . Очевидно, что , , ,. Матрица играет роль нуля. означает вектор-столбец или вектор-строку из нулей.

Квадратная матрица

с элементами при называется единичной. Очевидно, что . Матрица играет роль единицы. Только для нее последние равенства выполнены с любой матрицей . В самом деле, если бы для какой-то матрицы равенства были справедливы для любой матрицы , то мы имели бы и , откуда .

Матрица называется скалярной. Если – скалярная матрица, то равенство выполнено для любой матрицы .

Квадратная матрица называется диагональной; числа могут быть различными. Если , то – скалярная матрица; только в этом случае равенство выполнено для любой матрицы .

Задача. Приведите пример диагональной матрицы и некоторой матрицы , для которых . ¨

Задача. Докажите равенства

.¨