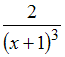- •Задание n 1 Тема: Сходимость числовых рядов
- •Задание n 2 Тема: Область сходимости степенного ряда
- •Задание n 3 Тема: Ряд Тейлора (Маклорена)
- •Задание n 4 Тема: Числовые последовательности
- •Задание n 5 Тема: Определение вероятности
- •Задание n 6 Тема: Законы распределения вероятностей дискретных случайных величин
- •Задание n 7 Тема: Числовые характеристики случайных величин
- •Задание n 8 Тема: Интервальные оценки параметров распределения
- •Задание n 9 Тема: Статистическое распределение выборки
- •Задание n 10 Тема: Точечные оценки параметров распределения
- •Задание n 11 Тема: Периодические функции
- •Задание n 12 Тема: Элементы гармонического анализа
- •Задание n 13 Тема: Ряд Фурье. Теорема Дирихле
- •Задание n 29 Тема: Гармонические колебания
- •Задание n 33 Тема: Ранг матрицы
- •Задание n 17 Тема: Линейные операции над матрицами
- •Задание n 18 Тема: Системы линейных уравнений
- •Задание n 19 Тема: Области на комплексной плоскости
- •Задание n 20 Тема: Дифференцирование функции комплексного переменного
- •Задание n 21 Тема: Формы записи комплексного числа
- •Задание n 22 Тема: Операции над комплексными числами
- •Задание n 23 Тема: Область определения функции
- •Задание n 24 Тема: Приложения дифференциального исчисления фоп
- •Задание n 25 Тема: Предел функции
- •Задание n 26 Тема: Свойства определенного интеграла
- •Задание n 27 Тема: Основные методы интегрирования
- •Задание n 28 Тема: Производные высших порядков
- •Задание n 31 Тема: Прямая и плоскость в пространстве
- •Задание n 32 Тема: Полярные координаты на плоскости
- •Задание n 33 Тема: Алгебраические операции
- •Задание n 34 Тема: Основные алгебраические структуры
- •Задание n 35 Тема: Линейные отображения
Задание n 26 Тема: Свойства определенного интеграла
1
Определенный
интеграл
 равен
…
равен
…
0
Решение:
Пусть
![]() Тогда
Тогда
![]() то
есть функция
то
есть функция
![]() является
нечетной. А определенный интеграл от
нечетной функции по симметричному
интервалу равен нулю.
является
нечетной. А определенный интеграл от
нечетной функции по симметричному
интервалу равен нулю.
2
Среднее
значение функции
![]() на
отрезке
на
отрезке
 равно
…
равно
…
![]()
Решение:
Среднее
значение функции
![]() ,
непрерывной на отрезке
,
непрерывной на отрезке
![]() ,
вычисляется по формуле
,
вычисляется по формуле
 где
где
![]() .
Тогда
.
Тогда

3
Определенный
интеграл
 равен
… 0
равен
… 0
Решение:
Пусть
![]() Тогда
Тогда
![]() то
есть функция
то
есть функция
![]() является
нечетной. А определенный интеграл от
нечетной функции по симметричному
интервалу равен нулю.
является
нечетной. А определенный интеграл от
нечетной функции по симметричному
интервалу равен нулю.
4
Для
определенного интеграла
 справедливо
равенство …
справедливо
равенство …

Решение:
Пусть
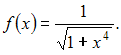 Тогда
Тогда
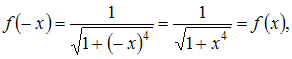 то
есть функция
то
есть функция
![]() является
четной. А определенный интеграл от
четной функции
является
четной. А определенный интеграл от
четной функции
![]() по
симметричному интервалу
по
симметричному интервалу
![]() можно
представить как
можно
представить как

Задание n 27 Тема: Основные методы интегрирования
1
Неопределенный
интеграл
![]() можно
представить как …
можно
представить как …

Решение:
Воспользуемся
методом интегрирования по частям
![]() .
Тогда
.
Тогда
![]()


2
Множество
первообразных функции
 имеет
вид …
имеет
вид …
|
|
|
|
|
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции. Тогда

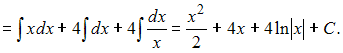
3
Множество
первообразных функции
 имеет
вид …
имеет
вид …
|
|
|
|
|
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции. Тогда
 Произведем
замену
Произведем
замену
![]() ,
,
![]() ,
,
![]() :
:

4
Множество
первообразных функции
 имеет
вид …
имеет
вид …
![]()
Решение:
Чтобы
определить множество первообразных,
вычислим неопределенный интеграл от
этой функции. Тогда
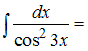 Произведем
замену
Произведем
замену
![]() ,
,
![]() ,
,
![]() :
:

Задание n 28 Тема: Производные высших порядков
1
Производная
второго порядка функции
![]() равна
…
равна
…

Решение:
Вычислим
производную первого порядка:
![]() Тогда
производная второго порядка вычисляется
как производная от производной первого
порядка, то есть
Тогда
производная второго порядка вычисляется
как производная от производной первого
порядка, то есть

2
Производная
третьего порядка функции
![]() равна
…
равна
…
|
|
|
|
|
Решение:
Вычислим
производную первого порядка:
![]() Вычислим
производную второго порядка как
производную от производной первого
порядка:
Вычислим
производную второго порядка как
производную от производной первого
порядка:
![]() Тогда
производная третьего порядка вычисляется
как производная от производной второго
порядка, то есть
Тогда
производная третьего порядка вычисляется
как производная от производной второго
порядка, то есть

3
Производная
второго порядка функции
![]() равна
…
равна
…
![]()
Решение:
Вычислим
производную первого порядка:
![]() Тогда
производная второго порядка вычисляется
как производная от производной первого
порядка, то есть
Тогда
производная второго порядка вычисляется
как производная от производной первого
порядка, то есть
ЗАДАНИЕ N 28
Тема: Прямая на плоскости
1
Расстояние
от точки
![]() до
прямой
до
прямой
![]() равно
… 6
равно
… 6
Решение:
Расстояние
от точки
![]() до
прямой
до
прямой
![]() найдем
по формуле
найдем
по формуле
 .
.
2
Угловой
коэффициент прямой, заданной уравнением
![]() ,
равен …
,
равен …
![]() Решение:
Выразим
из уравнения
Решение:
Выразим
из уравнения
![]() переменную
переменную
![]() ,
а именно
,
а именно
![]() .
Тогда угловой коэффициент
.
Тогда угловой коэффициент
![]() .
.
ЗАДАНИЕ N 30
Тема: Кривые второго порядка
1
Мнимая
полуось гиперболы
 равна
…
равна
…
2
Решение:
Каноническое
уравнение гиперболы имеет вид
 ,
где
,
где
![]() –
действительная полуось,
–
действительная полуось,
![]() -
мнимая полуось. Тогда
-
мнимая полуось. Тогда
![]() .
.
2
Эксцентриситет
гиперболы
 равен
… 2
равен
… 2
Решение:
Эксцентриситет
гиперболы
 вычисляется
по формуле
вычисляется
по формуле
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
 .
.
3
Уравнение
параболы имеет вид
![]() .
Тогда директриса задается уравнением
…
.
Тогда директриса задается уравнением
…
![]()
Решение:
Для
канонического уравнения параболы
![]() ,
где
,
где
![]() –
параметр параболы, уравнение директрисы
имеет вид
–
параметр параболы, уравнение директрисы
имеет вид
![]() .
То есть
.
То есть
![]() .
.