Задание n 8 Тема: Интервальные оценки параметров распределения

1

Точечная оценка среднего квадратического отклонения нормально распределенного количественного признака равна . Тогда его интервальная оценка может иметь вид …

Решение: Интервальной оценкой среднего квадратического отклонения нормально распределенного количественного признака служит доверительный интервал при , или при , где находят по соответствующей таблице приложений. Этому определению удовлетворяет интервал

2

Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна … 1,6

Решение: Точность интервальной оценки определяется как , то есть

Задание n 9 Тема: Статистическое распределение выборки

1

Из генеральной совокупности извлечена выборка объема , гистограмма частот которой имеет вид: Тогда значение параметра a равно …

24

Решение: Так как объем выборки вычисляется как , где , то

2

Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид:

Тогда значение параметра равно …

47

Решение: Объем выборки вычисляется по формуле , где – частота варианты . Тогда , то есть

3

Из генеральной совокупности извлечена выборка объема : Тогда относительная частота варианты равна …

Решение: Относительная частота вычисляется по формуле , где – частота варианты , а – объем выборки. Вычислим предварительно частоту варианты как . Тогда

Задание n 10 Тема: Точечные оценки параметров распределения

1

Из генеральной совокупности извлечена выборка объема : Тогда выборочное среднее квадратическое отклонение равно …

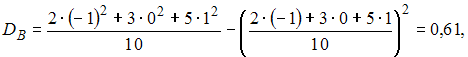Решение: Выборочное среднее квадратическое отклонение вычисляется как , где . Тогда и

2

Из генеральной совокупности извлечена выборка объема : Тогда выборочная дисперсия равна …

Решение: Выборочную дисперсию можно вычислить по формуле . Тогда

3

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 10, 12, 14. Тогда выборочная дисперсия равна …

Решение: Выборочная дисперсия вычисляется по формуле , где . Вычислив предварительно , получаем

Задание n 11 Тема: Периодические функции

1

Период функции равен …

Решение: Период функции равен . Тогда функция будет иметь период .

2

Период функции равен …

Решение: Период функции равен . Тогда функция будет иметь период .

3

Период функции равен …

Решение: Период функции равен . Тогда функция будет иметь период .

4

Период функции равен …

Решение: Период функции равен . Тогда функция будет иметь период .

5

Период функции равен …

Решение: Период функции равен . Тогда функция будет иметь период .

Задание n 12 Тема: Элементы гармонического анализа

1

Ортогональной к функции на [-;], не является функция …

Решение: Функции и называются ортогональными на [a, b], если . Из предложенных ответов этому условию не удовлетворяет функция , так как 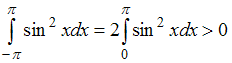. Для остальных функций , так как произведение будет нечетной функцией, а интеграл от нечетной функции по симметричному интервалу равен нулю.

2

Ортогональной к функции на [-;], не является функция …

Решение: Функции и называются ортогональными на [a, b], если . Из предложенных ответов этому условию не удовлетворяет функция , так как . Для остальных функций 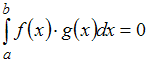, так как произведение будет нечетной функцией, а интеграл от нечетной функции по симметричному интервалу равен нулю.

3

Ортогональной к функции на [-1; 1], является функция …

Решение: Функции и называются ортогональными на [a, b], если . Поэтому функция в данной задаче должна быть нечетной, так как тогда произведение будет нечетной функцией. Интеграл от нечетной функции по симметричному интервалу равен нулю. Тогда в качестве искомой функции можно, например, использовать функцию .