
- •Задание n 1 Тема: Сходимость числовых рядов
- •Задание n 2 Тема: Область сходимости степенного ряда
- •Задание n 3 Тема: Ряд Тейлора (Маклорена)
- •Задание n 4 Тема: Числовые последовательности
- •Задание n 5 Тема: Определение вероятности
- •Задание n 6 Тема: Законы распределения вероятностей дискретных случайных величин
- •Задание n 7 Тема: Числовые характеристики случайных величин
- •Задание n 8 Тема: Интервальные оценки параметров распределения
- •Задание n 9 Тема: Статистическое распределение выборки
- •Задание n 10 Тема: Точечные оценки параметров распределения
- •Задание n 11 Тема: Периодические функции
- •Задание n 12 Тема: Элементы гармонического анализа
- •Задание n 13 Тема: Ряд Фурье. Теорема Дирихле
- •Задание n 29 Тема: Гармонические колебания
- •Задание n 33 Тема: Ранг матрицы
- •Задание n 17 Тема: Линейные операции над матрицами
- •Задание n 18 Тема: Системы линейных уравнений
- •Задание n 19 Тема: Области на комплексной плоскости
- •Задание n 20 Тема: Дифференцирование функции комплексного переменного
- •Задание n 21 Тема: Формы записи комплексного числа
- •Задание n 22 Тема: Операции над комплексными числами
- •Задание n 23 Тема: Область определения функции
- •Задание n 24 Тема: Приложения дифференциального исчисления фоп
- •Задание n 25 Тема: Предел функции
- •Задание n 26 Тема: Свойства определенного интеграла
- •Задание n 27 Тема: Основные методы интегрирования
- •Задание n 28 Тема: Производные высших порядков
- •Задание n 31 Тема: Прямая и плоскость в пространстве
- •Задание n 32 Тема: Полярные координаты на плоскости
- •Задание n 33 Тема: Алгебраические операции
- •Задание n 34 Тема: Основные алгебраические структуры
- •Задание n 35 Тема: Линейные отображения
Задание n 1 Тема: Сходимость числовых рядов
1
Даны
числовые ряды: А)
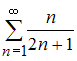 ,
В)
,
В)
 .
Тогда
…
.
Тогда
…
ряд А) расходится, ряд В) сходится
Решение:
Ряд
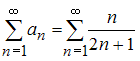 расходится,
так как для него не выполняется необходимое
условие сходимости. Действительно,
расходится,
так как для него не выполняется необходимое
условие сходимости. Действительно,
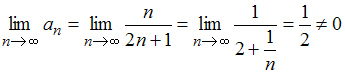 .
Для
исследования сходимости ряда
.
Для
исследования сходимости ряда
 применим
признак сходимости Даламбера. Тогда
применим
признак сходимости Даламбера. Тогда
 ,
то есть ряд сходится.
,
то есть ряд сходится.
2
Даны
числовые ряды:
А)
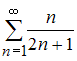 ,
В)
,
В)
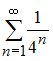 .
Тогда
… ряд А) расходится, ряд В) сходится
.
Тогда
… ряд А) расходится, ряд В) сходится
Решение:
Ряд
 расходится,
так как для него не выполняется необходимое
условие сходимости. Действительно,
расходится,
так как для него не выполняется необходимое
условие сходимости. Действительно,
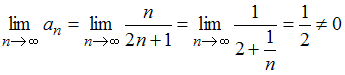 .
Для
исследования сходимости ряда
.
Для
исследования сходимости ряда
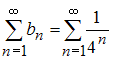 применим
признак сходимости Даламбера. Тогда
применим
признак сходимости Даламбера. Тогда
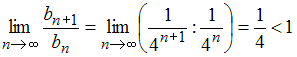 ,
то есть ряд сходится.
,
то есть ряд сходится.
3
Сумма
числового ряда
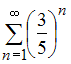 равна
…
равна
…
![]()
Решение:
Так
как
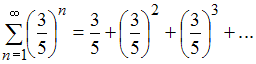 ,
то сумма данного ряда представляет
собой сумму бесконечно убывающей
геометрической прогрессии. То есть
,
то сумма данного ряда представляет
собой сумму бесконечно убывающей
геометрической прогрессии. То есть

4
Даны
числовые ряды:
А)
 ,
В)
,
В)
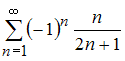 .
Тогда
…
.
Тогда
…
ряд А) сходится, ряд В) расходится
Решение:
Для
исследования сходимости знакочередующегося
ряда
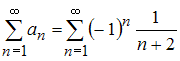 применим
признак сходимости Лейбница:
1) Вычислим
предел
применим
признак сходимости Лейбница:
1) Вычислим
предел
 .
2)
Для любого натурального
.
2)
Для любого натурального
![]() справедливо
справедливо
![]() ,
то есть последовательность
,
то есть последовательность
![]() монотонно
убывает.
Следовательно, ряд
монотонно
убывает.
Следовательно, ряд
 сходится.
Ряд
сходится.
Ряд
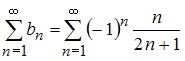 расходится,
так как
расходится,
так как
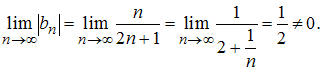
5
Даны
числовые ряды:
А)
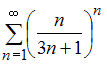 ,
В)
,
В)
 .
Тогда
… ряд А) сходится, ряд В) расходится
.
Тогда
… ряд А) сходится, ряд В) расходится
Решение:
Для
исследования сходимости ряда
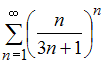 применим
радикальный признак сходимости Коши.
Тогда
применим
радикальный признак сходимости Коши.
Тогда
 ,
то есть ряд сходится.
Для исследования
сходимости ряда
,
то есть ряд сходится.
Для исследования
сходимости ряда
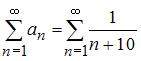 применим
теорему сравнения, для чего воспользуемся
расходящимся гармоническим рядом
применим
теорему сравнения, для чего воспользуемся
расходящимся гармоническим рядом
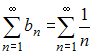 .
Тогда
.
Тогда
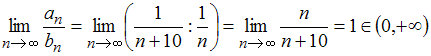 ,
то есть оба ряда расходятся или сходятся
одновременно. В нашем случае ряд
,
то есть оба ряда расходятся или сходятся
одновременно. В нашем случае ряд
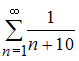 будет
расходится.
будет
расходится.
Задание n 2 Тема: Область сходимости степенного ряда
1
Область
сходимости степенного ряда
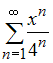 имеет
вид …
имеет
вид …
|
|
Решение:
Вычислим
предварительно радиус сходимости этого
ряда по формуле
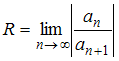 ,
где
,
где
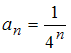 .
Тогда
.
Тогда
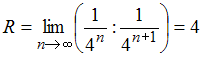 .
Следовательно, интервал сходимости
ряда имеет вид
.
Следовательно, интервал сходимости
ряда имеет вид
![]() .
Для
того чтобы найти область сходимости
степенного ряда, исследуем сходимость
ряда в граничных точках.
В точке
.
Для
того чтобы найти область сходимости
степенного ряда, исследуем сходимость
ряда в граничных точках.
В точке
![]() ряд
примет вид
ряд
примет вид
![]() .
Данный ряд расходится, так как не
выполняется необходимое условие
сходимости числового ряда:
.
Данный ряд расходится, так как не
выполняется необходимое условие
сходимости числового ряда:
![]() В
точке
В
точке
![]() получаем
знакочередующийся ряд
получаем
знакочередующийся ряд
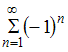 .
Аналогично получаем
.
Аналогично получаем
![]() ,
то есть ряд расходится.
Таким образом,
область сходимости ряда имеет вид
,
то есть ряд расходится.
Таким образом,
область сходимости ряда имеет вид
![]() .
.
2
Для
степенного ряда
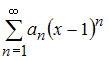 вычислен
предел
вычислен
предел
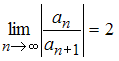 .
Тогда интервал сходимости данного ряда
имеет вид …
.
Тогда интервал сходимости данного ряда
имеет вид …
![]()
Решение:
Интервал
сходимости данного ряда определяется
как
![]() ,
где
,
где
![]() ,
,
![]() .
То есть
.
То есть
![]() ,
или
,
или
![]() .
.
3
Радиус
сходимости степенного ряда
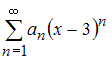 равен
7. Тогда интервал сходимости этого ряда
имеет вид …
равен
7. Тогда интервал сходимости этого ряда
имеет вид …
![]()
Решение:
Если
радиус сходимости степенного ряда
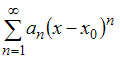 равен
равен
![]() ,
то его интервал сходимости примет вид
,
то его интервал сходимости примет вид
![]() .
Тогда интервал сходимости данного ряда
определяется как
.
Тогда интервал сходимости данного ряда
определяется как
![]() ,
или
,
или
![]() .
.
Задание n 3 Тема: Ряд Тейлора (Маклорена)
1
Если
![]() ,
то коэффициент
,
то коэффициент
![]() разложения
данной функции в ряд Маклорена по
степеням
разложения
данной функции в ряд Маклорена по
степеням
![]() равен
0
равен
0
Решение:
Так
как коэффициенты данного ряда вычисляются
по формуле
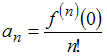 ,
то вычислим последовательно
производные:
,
то вычислим последовательно
производные:
![]()
![]()
![]() .
Тогда
.
Тогда
![]()
2
Ряд
Маклорена для функции
![]() имеет
вид …
имеет
вид …
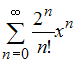 ,
,
![]()
Решение:
Так
как ряд Маклорена для функции
![]() имеет
вид
имеет
вид
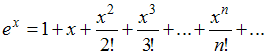 ,
при
,
при
![]() ,
то
,
то
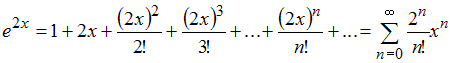 .
.
3
Если
![]() ,
то коэффициент
,
то коэффициент
![]() разложения
данной функции в ряд Тейлора по степеням
разложения
данной функции в ряд Тейлора по степеням
![]() равен
…
равен
…
![]()
Решение:
Так
как коэффициенты данного ряда Тейлора
вычисляются по формуле
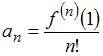 ,
то вычислим последовательно производные:
,
то вычислим последовательно производные:
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
4
Если
![]() ,
то коэффициент
,
то коэффициент
![]() разложения
данной функции в ряд Тейлора по степеням
разложения
данной функции в ряд Тейлора по степеням
![]() равен
… 4
равен
… 4
Решение:
Так
как коэффициенты данного ряда Тейлора
вычисляются по формуле
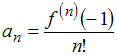 ,
то вычислим последовательно производные:
,
то вычислим последовательно производные:
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
.
