Лабораторная работа №2 Измерение емкости плоского конденсатора

Цель: измерить емкость плоского конденсатора.

Оборудование: генератор ГСФ-2, осциллограф С1-131/1-Д, плоский конденсатор, сигнальные провода.

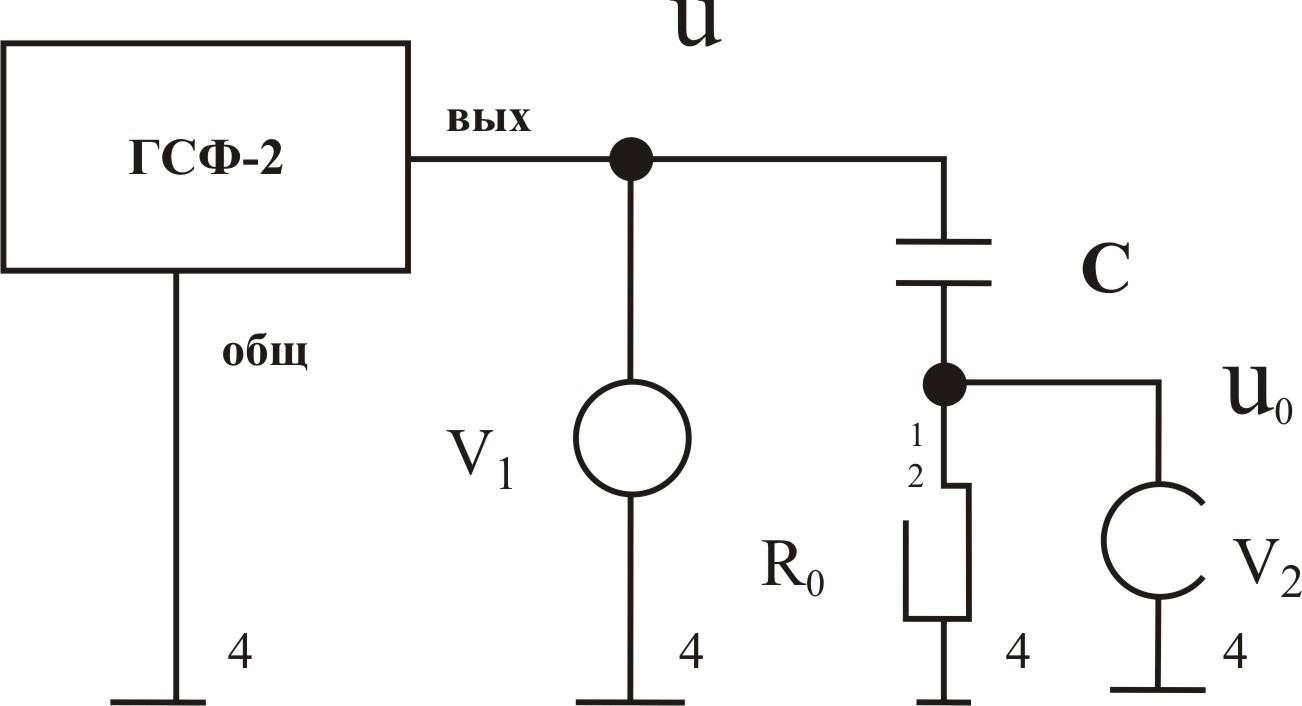
Рис.1. Схема измерения емкости плоского конденсатора при синусоидальном сигнале

Ход работы:

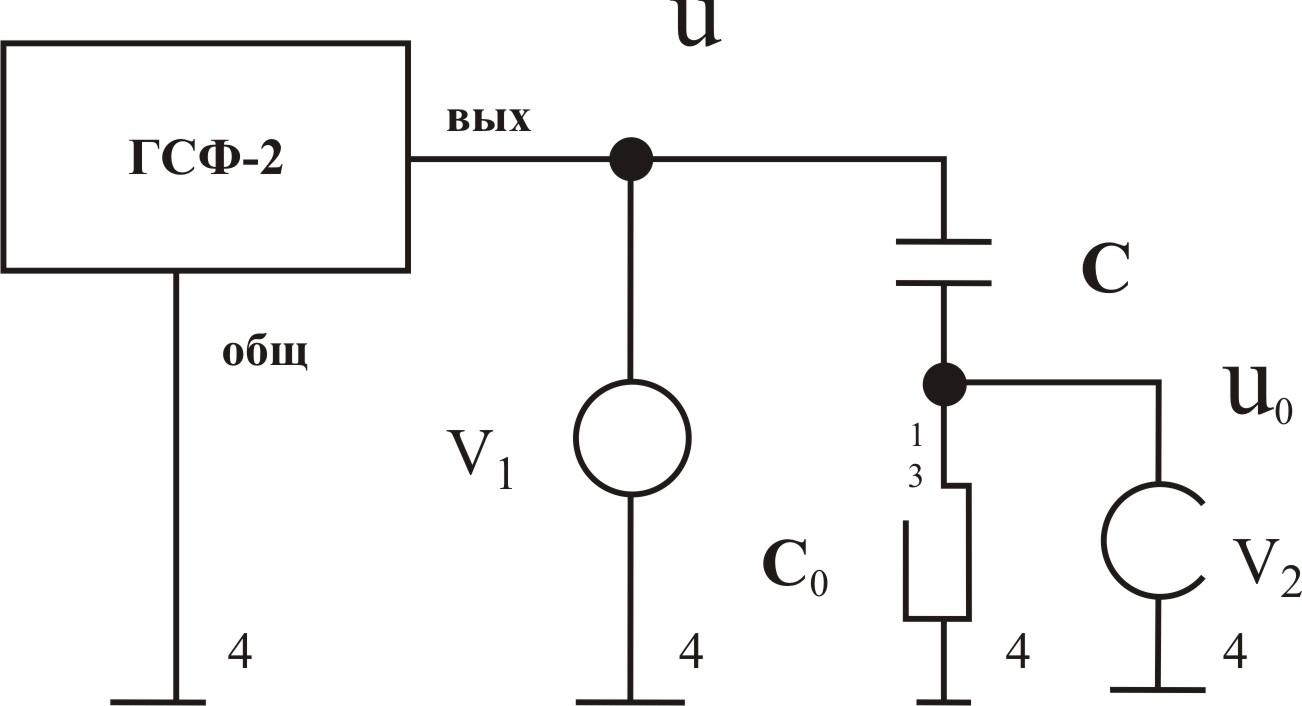
Рис.2. Схема измерения емкости плоского конденсатора при произвольной форме и частоте сигнала

Сначала подключаем приборы по схеме, изображенной на рисунке 1. Задаются на генераторе произвольные частота и напряжение. Снимаются показания с осциллографа:

U_m – амплитудное значение напряжения;

U – действующее значение напряжения;

U_R – напряжение на сопротивлении;

Uc – напряжение на конденсаторе.

Вычисляются значения Uc и емкость конденсатора с воздушным зазором C_B, используя значение частоты  установленной на генераторе, по следующим формулам:

Uc = (U² – U_R² )^0,5;

C_B = (U_R / Uc ) / ( 2   R₀ ) для схемы на рисунке 1;

C_B = (C₀ Uc₀) / ( U – Uc₀) для схемы на рисунке 2.

Показания приборов и необходимые вычисления вносим в таблицу 1.

Таблица 1

Показания приборов и вычисленные значения

N схемы	Ro, Ом	Um, В	v, Гц	U, В	Ur, В	Ucо,B	Uc, B	C, пФ
1
2

Находятся абсолютная Св_a и относительную погрешности Св значений измеренной емкости конденсатора.

Истинное значение емкости конденсатора обозначим Св_i. Оно находится по формуле:

Cв = ₀*S / d₀ = 112 пФ, тогда:

Св_a = Св_i – Св

Св = (Св_a / Св_i) * 100%

Таблица 2

Относительная и абсолютная погрешности вычислений емкости конденсатора

N схемы	Свi, пФ	∆Свa, пФ	∆Cв,%
1
2

По полученным результатам формулируются выводы.

Лабораторная работа №3 Измерение диэлектрической проницаемости веществ

Цель: измерить диэлектрическую проницаемость различных веществ.

Оборудование: генератор ГСФ-2, осциллограф С1-131/1-Д, плоский конденсатор, пластины из диэлектрика: (стекло, оргстекло, текстолит), сигнальные провода.

Ход работы:

ГСФ-2

Рис.1. Схема измерения емкости плоского конденсатора при синусоидальном сигнале с частотой 

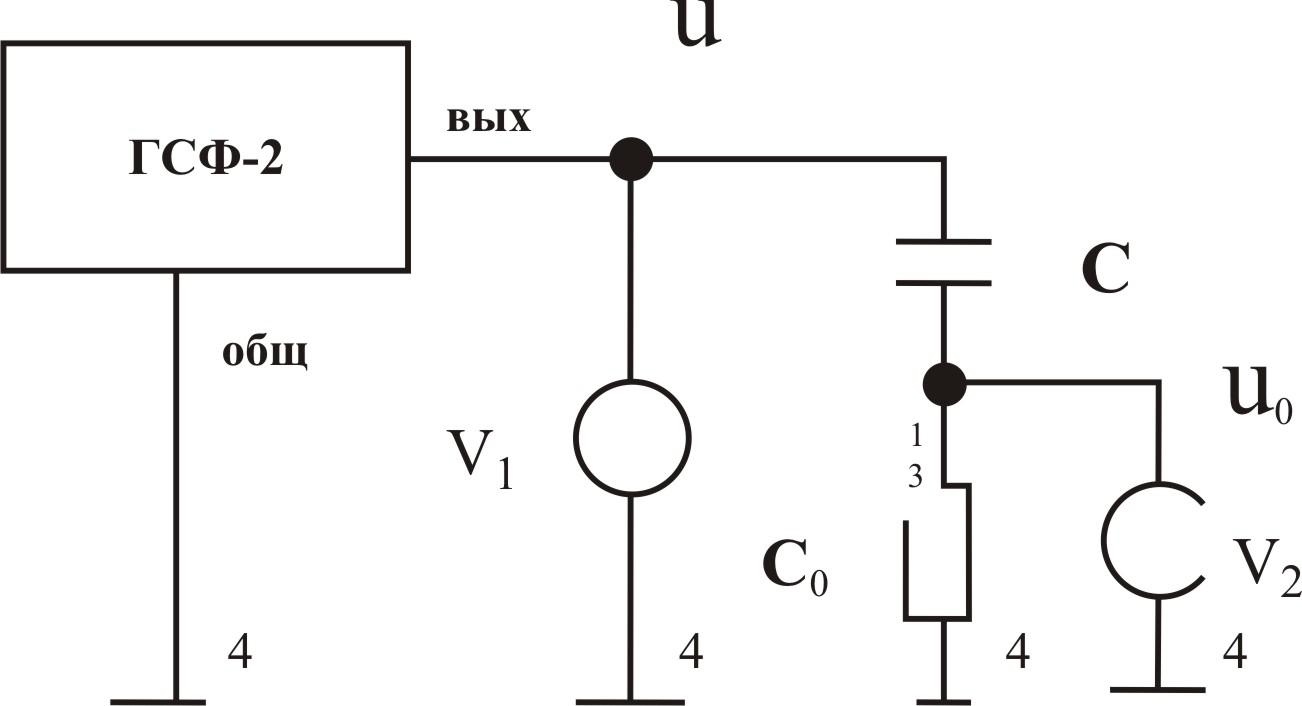
Рис.2. Схема измерения емкости плоского конденсатора при произвольной форме и частоте сигнала

Сначала подключаем приборы по схеме, изображенной на рисунок 1. Задаются на генераторе произвольные частота и напряжение. Снимаются показания с осциллографа:

U_m – амплитудное значение напряжения;

U – действующее значение напряжения находится по формуле;

U_R – напряжение на сопротивлении;

Uc₀ – напряжение на конденсаторе;

С – емкость плоского конденсатора.

Сравнивая емкость С конденсатора без диэлектрика (с воздушным зазором d₀ ) с емкостью С конденсатора с диэлектриком толщиной d между обкладками, находят диэлектрическую проницаемость  вещества диэлектрика:

₁ = (С₁/С_В)*(d/d₀).

С₁ и С_В находим по формулам:

С₁ = ( U_Rо / Uc ) / ( 2   R₀ ), где известно, что d₀ = 1,8 мм, C₀ = 10,2 нФ,

С_В – емкость конденсатора без диэлектрика с воздушным зазором.

Для ₂ формула аналогична, только вместо С₁ надо взять С₂, равное:

С₂ = (С₀*U_C0)/(U – U_C0), где известно, что C₀ = 10,2 нФ.

Таблица 1