Заключение

В курсовой работе была построена динамическая модель иглы в замке механизма. С помощью нее были определены все силы, действующие на иглу. Затем была сформирована математическая модель движения иглы в замке вязального механизма, по которой был выполнен закон синтеза по варианту задания номер 23, представленного в таблице 3 [5]. Для анализа движения были построены графики. По ним были проанализированы все величины перемещений, деформаций и сил.

К замкам вязального механизма с подвижными иглами предъявляется одно из важных требований: конструкция замков должна быть надежна в эксплуатации, должна обеспечивать длительную работу машины без перебоев.

Сравнив графики на рисунках 9 и 11,10 и 12, стало ясно, что жесткость влияет на амплитуду и период колебаний. При уменьшении жесткости уменьшается амплитуда и увеличивается период. В данном случае амплитуда увеличилась в 0, 44 раза, а период в 1,1 раз. Снижение жесткости приводит к улучшению динамических качеств иглы в замке вязального механизма, но при этом увеличивается ускорение и силы в замке вязального механизма. Уменьшенная амплитуда приводит к более плавному процессу петлеобразования. Поэтому, следует повышать жесткость иглы, чтобы избежать ее скорой поломки, либо уменьшать жесткость пружины для повышения динамики сил.

Список использованных источников

1. Антонов, Г.К., Антонов, А.Г. Ремонт и обслуживание отечественных и зарубежных ручных трикотажных машин/ Г.К. Антонов, А.Г. Антонов. – М.; Л.: Легпромбытиздат, 1992. –144 с.

2. Гарбарук, В. Н. Проектирование трикотажных машин/ В. Н. Гарбарук. – М.; Л.: Машиностроение, 1980. –472 с.

3. Вульфсон, И. И. Динамические расчеты цикловых механизмов / И. И. Вульфсон. – Л.: Машиностроение, 1976. –328 с.

4. Поршнев, С. В. MATLAB 7. Основы работы и программирования: учебник / С. В. Поршнев. –М.: ООО «Бином-Пресс», 2006.

5. Анашкина, Е. В, Бабкина Н. М., Беспалова И. М., Мазин Л. С., Марковец А. В. Методические указания по выполнению курсовой работы по дисциплине «Математические модели механизмов машин и моделирование на ЭВМ»/ Е. В Анашкина, Н. М. Бабкина, И. М. Беспалова, Л. С. Мазин, А. В. Марковец. Отпечатано в типографии СПБГУТД, –28 с.

Приложение А

Блок-схема головного модуля

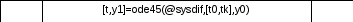
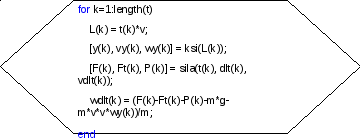
Приложение Б

Блок-схема подпрограммы вычисления зависимости ksi(L) и ее первой и второй передаточной функции

Да

Нет

Да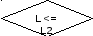

Нет

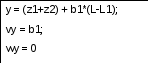
Приложение В

Блок-схема подпрограммы вычисления сил, действующих в модели

Вычисление зависимости изменения знака vx

Приложение Г

Блок-схема подпрограммы вычисления правых частей системы дифференциальных уравнений

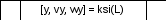
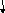
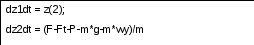
Приложение Д

Программа моделирования динамики иглы в замке вязального механизма на языке программирования системы MATLAB

function igla_okr

% IGLA_OKR - программа моделирования движения иглы по кулирному клину.

% Первый участок - косинусоида

% Второй участок - прямая

% Третий участок - синусоида

% Глобальные переменные программы

global c b dlt1 m Ft0 P0 g v mu

global b1 z1 z2 z3

global L1 L2 L3

global m1 n s

% Параметры участков клина

z1 = 2.23e-03;

z2 = 7.00e-03;

z3 = 14.04e-03;

Bt = 45;

b1 = tan((180-Bt)*pi/180);

% Параметры динамической модели

c = 1e+04;

psi = 0.6;

dlt1 = 0.24e-03;

m = 0.713e-03;

Ft0 = 0.24;

P0 = 0.1;

g = 9.81;

v = 0.7;

w = sqrt(c/m);

b = c*psi/(2*pi*w);

mu = 100000;

% Определение законов движения по участкам

% Первй участок - косинусоида

m1=z3;

n=z1+z2-z3;

L1 = pi*n/(2*b1)

% Второй участок - прямая

L2 = L1 - z2/b1

% Третий участок - синусоида

s=z1;

L3 = L2 - 2*z1/b1

% Задание интервала интегрирования

t0 = 0; tk = L3/v;

% Начальные условия

y0 = [0, 0];

% Интегрирование дифференциального уравнения математической модели

[t,y1] = ode45(@sysdif, [t0, tk], y0);

% Транспонирование массива времени

t = t';

% Выделение из двумерного массива y1 массивос dlt (деформация) и vdlt

% (скорость деформации в зазоре)

dlt = y1(:,1)';

vdlt = y1(:,2)';

% Вычисление сил, действующих в зазоре игла-клин и ускорения деформации для

% построения графиков

for k=1:length(t)

L(k) = t(k)*v;

[y(k), vy(k), wy(k)] = ksi(L(k));

[F(k), Ft(k), P(k)] = sila(t(k), dlt(k), vdlt(k));

wdlt(k) = (F(k)-Ft(k)-P(k)-m*g-m*v*v*wy(k))/m;

end;

% Построение графиков законов движения иглы

figure(1)

subplot(311); plot(L, y, '-k', 'LineWidth', 2);

grid on, xlabel('L, m'), ylabel('\xi, m');

subplot(312); plot(L, vy*v, '-k', 'LineWidth', 2);

grid on, xlabel('L, m'), ylabel('\xi\prime, m/c');

subplot(313); plot(L, wy*v^2, '-k', 'LineWidth', 2);

grid on, xlabel('L, m'), ylabel('\xi\prime\prime, m/c^2');

% Построение графиков зависимостей деформации, скорости и ускоерния

% деформации в зазоре игла-клин

figure(2)

subplot(311), plot(t, dlt, '-k', 'LineWidth', 2), grid on

xlabel('t, c'), ylabel('\Delta, m')

subplot(312), plot(t, vdlt, '-k', 'LineWidth', 2), grid on

xlabel('t, c'), ylabel('\Delta\prime, m/c')

subplot(313), plot(t, wdlt, '-k', 'LineWidth', 2), grid on

xlabel('t, c'), ylabel('\Delta\prime\prime, m/c^2')

% Построение графика зависимости силы в зазоре игла-клин

figure(3);

subplot(311), plot(t, Ft, '-k', 'LineWidth', 2), grid on

xlabel('t, c'), ylabel('Ft, H')

subplot(312), plot(t, P, '-k', 'LineWidth', 2), grid on

xlabel('t, c'), ylabel('P, H')

subplot(313), plot(t, F, '-k', 'LineWidth', 2), grid on

xlabel('t, c'), ylabel('F, H')

%=======================================================

% ПОДПРОГРАММЫ

%=======================================================

% Подпрограмма вычисления зависимости ksi(L) и ее первой и второй

% передаточных функций

function [y, vy, wy] = ksi(L)

% Описание глобальных параметров

global L1 L2 L3 m1 n s b1 z1 z2 z3

% Перебор участков

if L <= L1

% Первый участок

y = m1+n*(1-cos((pi/2)*(L/L1)));

vy = ((pi*n)/(2*L1))*sin((pi/2)*(L/L1));

wy = ((pi^2*n)/(4*L1^2))*cos((pi/2)*(L/L1));

elseif L >= L2

% Если движение на третьем участке

y = -s*((L-L3)/(L3-L2)-(1/pi)*sin((pi*(L-L3))/(L3-L2)));

vy = -(s/(L3-L2))*(1-cos((pi*(L-L3))/(L3-L2)));

wy =-((s*pi)/((L3-L2)^2))*sin((pi*(L-L3))/(L3-L2));

else

% Если движение на втором участке

y = (z1+z2) + b1*(L-L1);

vy = b1;

wy = 0;

end

% -----------------------------------------------------

% Подпрограмма вычисления сил, действующих в модели

function [F, Ft, P] = sila(t, dlt, vdlt)

% Описание глобальных параметров

global c b dlt1 m Ft0 P0 g v mu

% Вычисление силы F

if(dlt<0)

F=-c*dlt-b*vdlt;

elseif (dlt>=0 & dlt<=dlt1)

F=0.0;

else

F=-c*(dlt-dlt1)-b*vdlt;

end

% Вычисление внешнего кинематического воздействия

L = v*t;

[y, vy, wy] = ksi(L);

vx = v*vy + vdlt;

% Вычисление зависимости изменения знака vx

k = sign(vx);

zn = k*(1-exp(-k*mu*vx));

% Сила трения

Ft = Ft0*zn;

% Сила полезного сопротивления

P = P0*zn;

% -----------------------------------------------------

% Подпрограмма вычисления правых частей системы дифференциальных уравнений

function dzdt = sysdif(t, z)

% Описание глобальных параметров

global m v g

% Вычисление внешнего кинематического воздействия

L = v*t;

[y, vy, wy] = ksi(L);

vy = v*vy;

wy = v^2*wy;

% Вычисление сил, действующих в модели

[F, Ft, P] = sila(t, z(1), z(2));

% Вычисление правых частей

dz1dt = z(2);

dz2dt = (F-Ft-P-m*g-m*wy)/m;

% Формирование выходного массива

dzdt = [dz1dt; ...

dz2dt];

41