Математическая модель движения иглы в замке вязального механизма

Перейдем к составлению математической модели рассматриваемой системы по выбранной модели, изображенной на рисунке 5. Для этой цели удобно воспользоваться уравнением Лагранжа ΙΙ рода [3] в форме

, (2)

где Т – кинетическая энергия иглы; Q_z – активная сила, действующая на иглу вдоль обобщенной координаты z.

Нетрудно показать, что

, (3)

где m – масса иглы.

Элементарная работа δА активных сил на возможных перемещениях может быть представлена в виде

. (4)

C учетом (1) – (4) математическая модель рассматриваемой системы в установочном положении может быть записана в виде

, (5)

при t=0 Δ_*(0)=0, .

Запишем аналитические выражения всех сил, входящих в правую часть уравнения (5). При рассмотрении движения пятки иглы относительно клиньев ее поверхность принята упруго-деформирующей. Таким образом, сила, действующая на иглу со стороны пружины с элементом типа «люфт» вдоль направления движения иглы, может быть принята равной

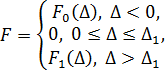, (6)

Δ=Δ_* –Δ₀,

где Δ – величина деформации пружины с учетом элемента типа «люфт»;Δ₁ – максимальная величина зазора в паре игла – клин; Δ₀ – длина пружины с учетом элемента типа «люфт» в установочном положении;

,

Δ,

где с – приведенная жестккость материала иглы, b – коэффициент демпфирования.

Будем считать, что сила трения,возникающая при движении иглы в пазу игольницы,в первом приближении имеет вид

, (7)

где F_тр – амплитудное значение силы трения.

Сила технологического сопротивления пропорциональна усилию оттяжки и зависит от знака скорости движения иглы и имеет вид

, (8)

где Р₀ – усилие оттяжки.

Выражение (5) с учетом (6)-(8) представляет собой математическую модель движения иглы в замке вязального механизма.

Синтез закона движения иглы

Исходными данными для проектирования клина являются величины подъема (для заключающего клина) или опускания иглы (для кулирного клина) на каждом участке, а также углы наклона прямолинейных участков клиньев. Величина z₁ соответствует необходимому перемещению иглы из ее нижнего положения до уровня отбойной плоскости О – О. Величина z₂ соответствует необходимому перемещению иглы в момент сбрасывания. Величина z₃ соответствует максимальному перемещению иглы. Угол наклона прямолинейного участка кулирного клина – β_к.

На рисунке 6 изображена одна из возможных форм кулирного клина. Кулирный клин служит для опускания иглы. Траектория кулирного клина имеет конфигурацию, состоящую из трех участков. Криволинейная траектория Ι участка обеспечивает плавное опускание иглы из положения заключения до момента прессования. За это время происходит прокладывание нити и ее вынесение под крючок иглы. Криволинейная траектория на этом участке позволяет снизить вертикальную скорость иглы в момент окончания прессования и избежать поломок язычка иглы. На ΙΙ участке перемещение с постоянной скоростью обеспечивает быстрый спуск иглы вниз до уровня отбойной плоскости О – О. При этом угол наклона траектории прямолинейного участка к горизонтали равен 2π– β_к, где β_к – угол кулирования. Криволинейная траектория ΙΙΙ участка обеспечивает плавное опускание иглы до момента оттяжки.

Как видно из рисунка 6, кулирный клин имеет центральный участок с прямолинейным профилем, сопряженный переходными криволинейными участками. В качестве криволинейных участков целесообразно проанализировать законы движения с использованием кривых 3-го и 4-го порядков.

Запишем аналитические выражения функций положения.

На Ι участке, изображенном на рисунке 6, кривая имеет форму косинусоиды. Закон движения для криволинейного профиля Ι участка записывается в следующем виде

,

где – текущая длина участка.

Тогда закон движения примет вид

, (9)

найдем производную по l от данного закона движения

. (10)

В рассматриваемом случае неизвестными являются m₁, n и l₁. Для их определения воспользуемся граничными условиями в виде

при l=0 ;

при l=l₁ (11)

Подставив данные граничные условия (11) в формулы (9) и (10), получим

,

.

,

.

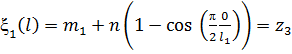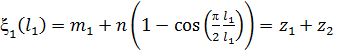После преобразования найдем

, , . (12)

Рассмотрим участок ΙΙ. На участке ΙΙ игла движется по прямой линии. Для прямолинейного участка ΙΙ закон движения иглы имеет вид

. (13)

Коэффициент b₁=tgβ_k, величина λ₂=l₁. На этом участке неизвестными величинами являются a и l₂. Для их определения необходимо составить граничные условия

при l=l₁ ;

при l=l₂ . (14)

Подставляя (14) в выражение (13), получим

,

. (15)

Решая (15), найдем

, .

Таким образом, на участке ΙΙ закон имеет вид

.

Рассмотрим участок ΙΙΙ. На данном участке закон движения иглы соответствует синусоиде и может быть записан в виде

,

где .

После подстановки закон движения примет вид

,

найдем производную от данного закона движения

.

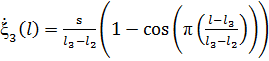Граничные условия записываются в виде

при l=l₂ ;

при l=l₃ .

С учетом граничных условий нетрудно получить, что

,

,

,

.

На данном участке неизвестные величины r, s и l₃. Найдем их, решив (20)

.

Рисунок 6 – Форма кулирного клина

Введем полученные данные в таблицу 1.