41. Сложение взаимно – перпендикулярных колебаний.

Сложение двух взаимно перпендикулярных колебаний: 1. Круговые частоты и фазы одинаковы, амплитуды различны: x=A₁ sin , y=A₂ sin где x и y - смещения тела, вызванные первым и вторым колебаниями. Тогда . .

Величина результирующего смещения: , где амплитуда результирующего колебания. 2. Круговые частоты одинаковы, фазы различаются на , амплитуды различны: x=A₁ sin , y=A₂ sin , тогда. Это уравнение Эллипса.

Следовательно, результирующее движение тела совершается по эллипсу, полуось которого равны амплитудам слагаемых колебаний. Если A1=A2=A, то уравнение эллипса переходит в уравнение окружности, и тело будет описывать окружность.

42. Осциллятор с затуханием.

В качестве модели консервативного гармонического осциллятора возьмём груз массы m, закреплённый на пружине жесткостью k. Пусть x - это смещение груза относительно положения равновесия.

Взяв за основу ту же модель, добавим в нее силу вязкого трения. Сила вязкого трения направлена против скорости движения груза относительно среды и пропорциональна этой скорости. Тогда полная сила, действующая на груз, записывается так:

Проводя аналогичные действия, получаем дифференциальное уравнение, описывающее затухающий осциллятор.

Здесь введено обозначение: 2γ = α / m. Коэффициент γ носит название постоянной затухания. Он тоже имеет размерность частоты.

Решение же распадается на три случая.

• При малом трении (γ < ω₀) общее решение записывается в виде:

x(t) = Ae ^{− γt}sin(ω_ft + φ), где - частота свободных колебаний.

• Затухание γ = ω₀ называют критическим. Начиная с такого значения показателя затухания, осциллятор будет совершать так называемое неколебательное движение. В граничном случае движение происходит по закону:

x(t) = (A + Bt)e ^{− γt}

• При сильном трении γ > ω₀ решение выглядит ещё по-другому.

, где

Критическое затухание примечательно тем, что именно при критическом затухании осциллятор быстрее всего стремится в положение равновесия. Если трение меньше критического, он дойдет до положения равновесия быстрее, однако "проскочит" его по инерции, и будет совершать колебания. Если трение больше критического, то осциллятор будет экспоненциально стремиться к положению равновесия, но тем медленнее, чем больше трение.

Поэтому в стрелочных индикаторах (например, в амперметрах) обычно стараются ввести именно критическое затухание, чтобы прочитать его показания можно было максимально быстро.

43. Добротность, декремент затухания

Это отношение называют декрементом затухания, а его логарифм — логарифмическим декрементом затухания:

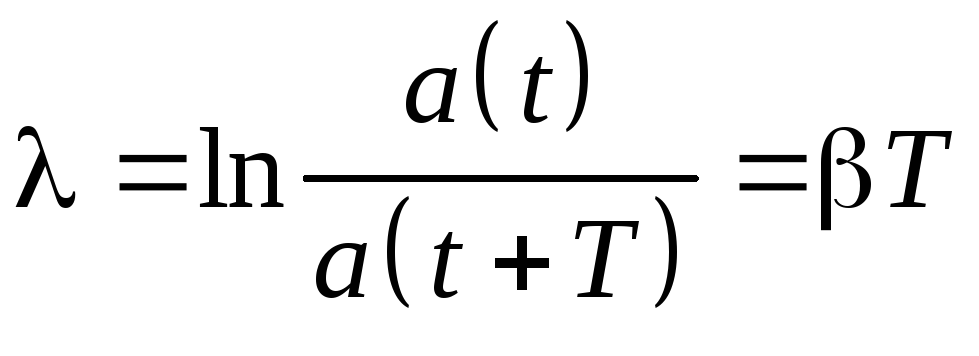
Для характеристики колебательной системы обычно используется логарифмический декремент затухания λ. Выразив в соответствии с (3.28) β через λ, и T, можно закон убывания амплитуды со временем записать в виде

За время τ, за которое амплитуда уменьшается в е раз, система успевает совершить N_e = τ/T колебаний. Из условия получается, что . Следовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за то время, за которое амплитуда уменьшается в e раз.

Для характеристики колебательной системы часто употребляется также величинаназываемая добротностью колебательной системы. Как видно из ее определения, добротность пропорциональна числу колебаний N_e, совершаемых системой за то время τ, за которое амплитуда колебаний уменьшается в e раз.

Затухание осциллятора также часто характеризуют безразмерным параметром, называемым добротностью. Добротность обычно обозначают буквой Q. По определению, добротность равна:

Чем больше добротность, тем медленнее затухают колебания осциллятора.

У осциллятора с критическим затуханием добротность равна 0,5. Соответственно, добротность указывает характер поведения осциллятора. Если добротность больше 0,5, то свободное движение осциллятора представляет собой колебания; со временем он пересечёт положение равновесия неограниченное количество раз. Добротность меньше или равная 0,5 соответствует неколебательному движению осциллятора; в свободном движении он пересечёт положение равновесия не более одного раза.

Добротность иногда называют коэффициентом усиления осциллятора, так как при некоторых способах возбуждения при совпадении частоты возбуждения с резонансной амплитуда колебаний оказывается примерно в Q раз больше, чем при возбуждении на низкой частоте.

Также добротность примерно равна количеству колебательных циклов, за которое амплитуда колебаний уменьшается в e раз, умноженному на π.

В случае колебательного движения затухание еще характеризуют такими параметрами, как:

• Время жизни колебаний, оно же время затухания. τ - время, за которое амплитуда колебаний уменьшится в e раз.

τ = 1 / γ

Это время можно рассматривать как время, необходимое для затухания колебаний (хотя формально свободные колебания продолжаются бесконечно долго).

• Логарифмический декремент затухания. Определяется как логарифм отношения двух последовательных максимальных отклонений в одну сторону. . Величина, обратная d, есть количество колебаний, которое пройдёт за время затухания τ.