18. Моменты инерции тонкого диска относительно его главных центральных осей.

     Для расчета моментов инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис.32). Определим момент инерции тонкого однородного диска относительно оси z , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r и наружным r+dr. Площадь такого кольца ds=2r $\pi$ dr, а его масса , где S= $\pi$ R² - площадь всего диска. Момент инерции тонкого кольца найдется по формуле dJ=dmr². Момент инерции всего диска определяется интегралом

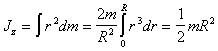    (п.18)

     Для определения J_x воспользуемся симметрией диска (J_x=J_y) и утверждением (п.10), полученным при расчете момента инерции прямоугольной пластины. При этом из (п.10) получаем J_z=2J_x    (п.19)

Откуда     (п.20)

17. Определение момента инерции тонкого стержня, относительно оси, проходящей через его середину.

     Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рис.27), масса которых . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции , т.е.      Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим

    (п.1)

     Это выражение может быть получено и другим способом, с помощью метода подобия. Будем считать, что рассматриваемый стержень состоит из двух половин (рис.28). Каждая из них имеет массу m/2 и длину l/2 .

Выражение для момента инерции стержня должно включать его массу и длину, так как это единственные параметры, определяющие его инерционные свойства при вращении. Пусть     (п.2)

где k- неизвестный коэффициент.      Для каждой из половин стержня при вращении вокруг оси AA^` можно найти момент инерции, используя (п.2) и теорему Гюйгенса-Штейнера.     (п.3)

Полный момент инерции стержня 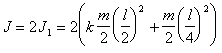    (п.4)

Но этот же момент инерции, согласно (п.2) равен kml². Приравнивая (п.4) и (п.2) имеем     (п.5)

или и, следовательно,     (п.6)

т.е. , что совпадает с (п.1)

1.Основные кинематические понятия. Материальная точка. Система отсчета, система координат.

Механика – наз-ся раздел физики, изучающий закономерности взаимодействия простейших форм движения материи.

Механическое движение – взаимное перемещение тел в пространстве в зависимости от времени.

Кинематика – описывает движение тел в пространстве и времени без выяснения причин их движения.

Материальная точка – это тело размерами которого в процессе движения можно пренебречь. Возможность рассматривать тело как материальную точку зависит не от самого тела, а от характера его движения. Например, при движении Земли вокруг солнца Землю можно считать мат.точкой, если же нас интересует суточное вращение Земли – то нельзя.

Тело отсчета – тело, относительно которого изучается движение рассм-его тела.

Система отсчёта – это тело или совокупность тел, по отношению к которым рассматривается движение других тел. С.О. состоит из тел отсчета, связанной с ним системой координат и прибором для измерения времени (часы).

Радиус-вектор – вектор(r), харак-щий изм-е положения точки за рассм-ый промежуток t.

Вектор перемещения – вектор, харк-щий изменение положения точки за рассм-ый промежуток t.

Система координат – а) если тело движется вдоль прямой линии, то его движение определяется 1 координатой

б) при движении в нек. плоскости:2 координаты

в) при движении в пространстве: 3 координаты