лабораторная работа / lab2

Саратовский государственный

Технический университет

Балаковский институт техники, технологии и управления

Кафедра УИТ

ТАУ

Лабораторная работа №2

Выполнил: ст.гр. УИТ-42

Синегубов А.А

Проверил:

Мефедова Ю.А

Балаково 2004

Вариант № 21

Цель работы: Ознакомление с методикой построения корневых годографов для анализа и синтеза линейных систем автоматического управления в системе Matlab.

Создадим ZPK-объект, найдем полюса и нули разомкнутой системы:

s=zpk('s');

w=(0.05^2*s^2+2*0.05*0.3*s+1)/(s*(0.1^2*s^2+2*0.1*0.3*s+1)*(0.01*s+1)*(0.01*s+1)^2)

Zero/pole/gain:

250000 (s^2 + 12s + 400)

-----------------------------

s (s+100)^3 (s^2 + 6s + 100)

Найдем полюса данной функции:

pole(w)

ans =

1.0e+002 *

0

-0.0300 + 0.0954i

-0.0300 - 0.0954i

-1.0000

-1.0000

-1.0000

Найдем нули данной функции:

zero(w)

ans =

-6.0000 +19.0788i

-6.0000 -19.0788i

Построим диаграммы Боде, корневой годограф:

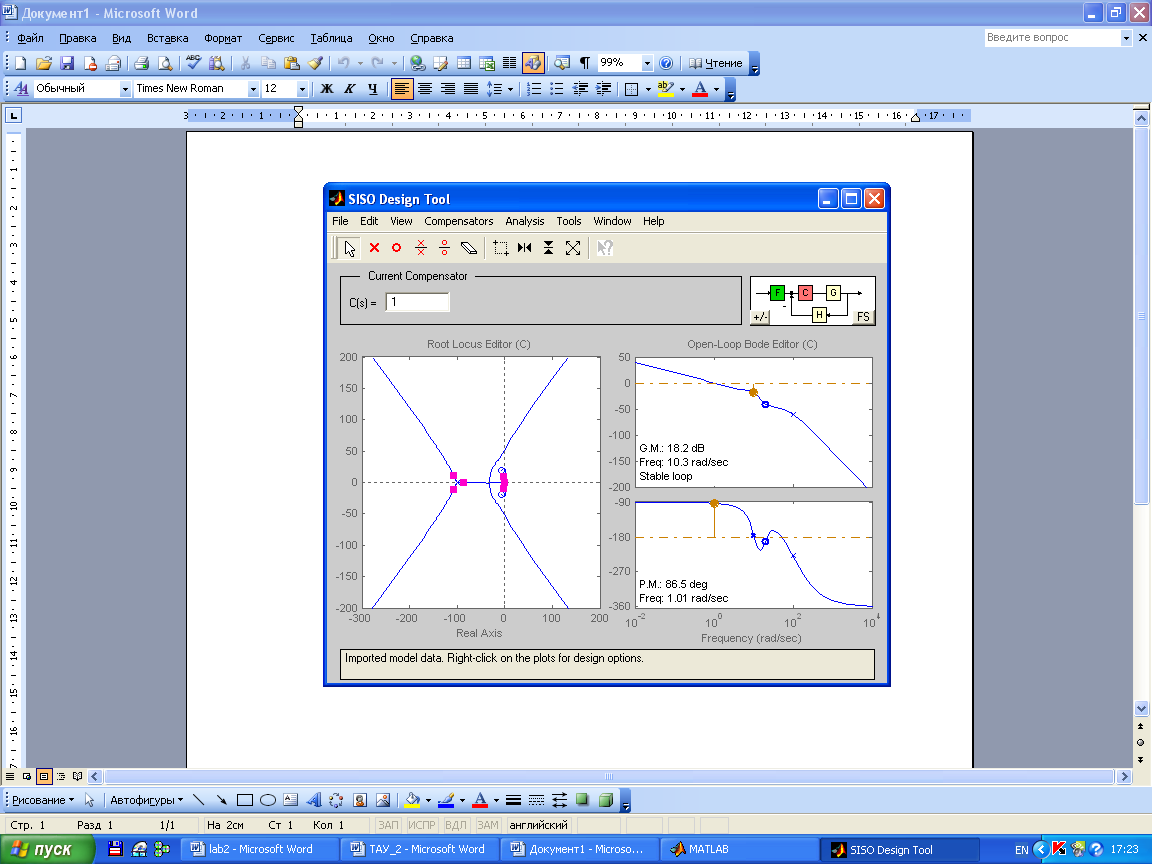
Построим переходный процесс:

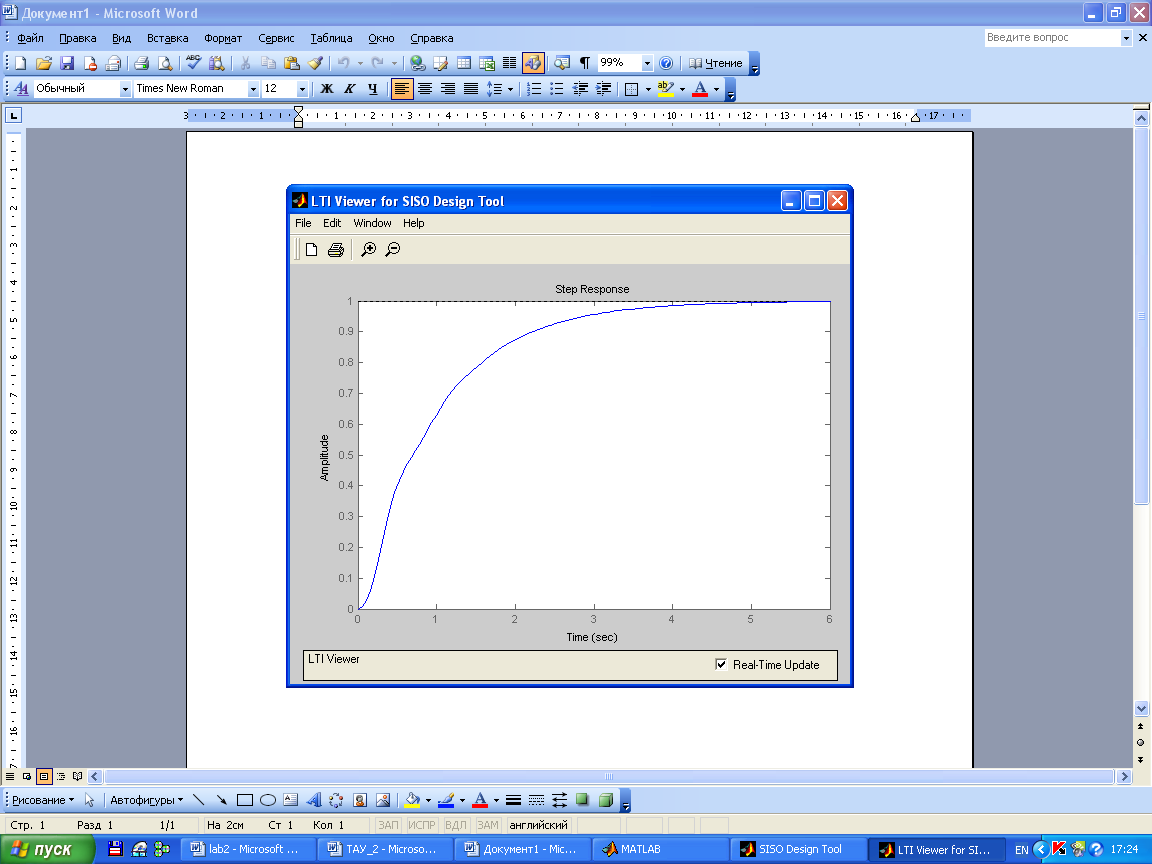
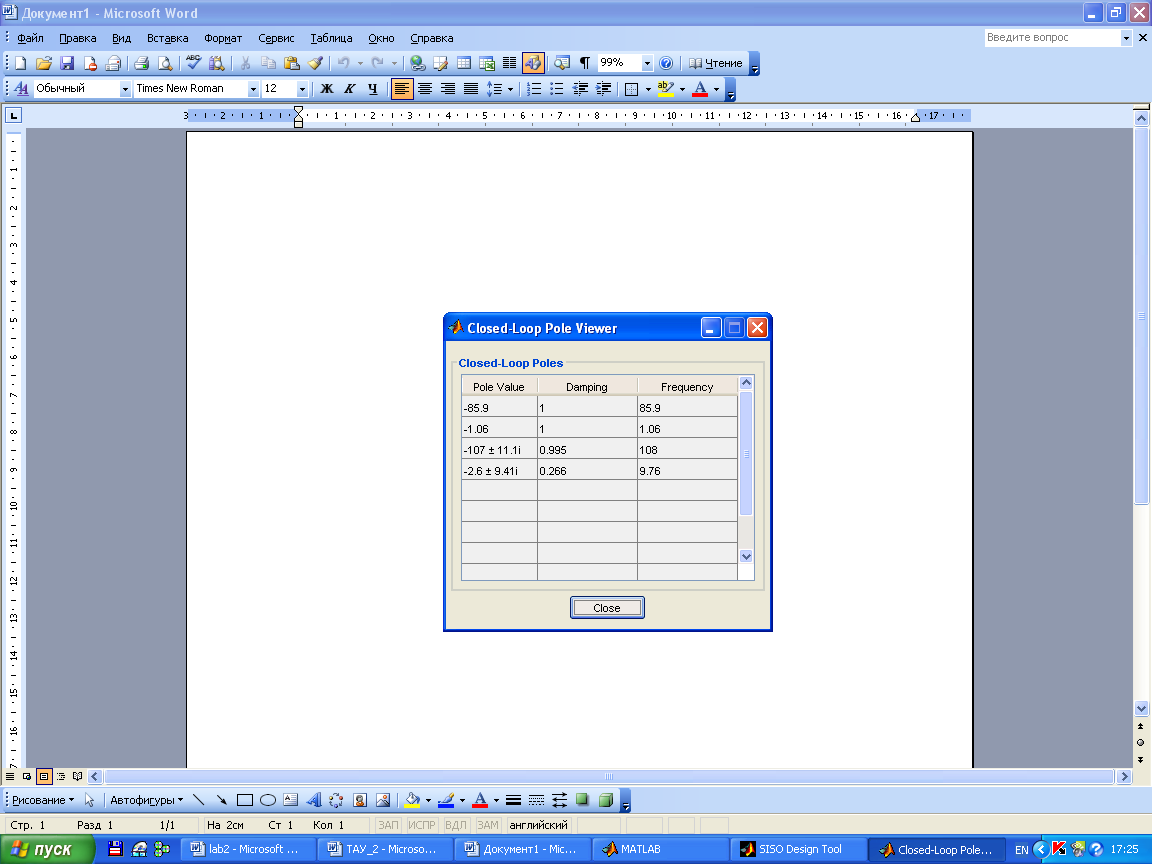
Из графиков видно, что система устойчива. Так же это видно из графика корневого годографа, т.к корни находятся в левой полуплоскости, что свидетельствует об устойчивости системы.

Захватив корни, найдем K^кр. Построим корневой годограф и диаграмму Боде:

K^кр≈ 7,54

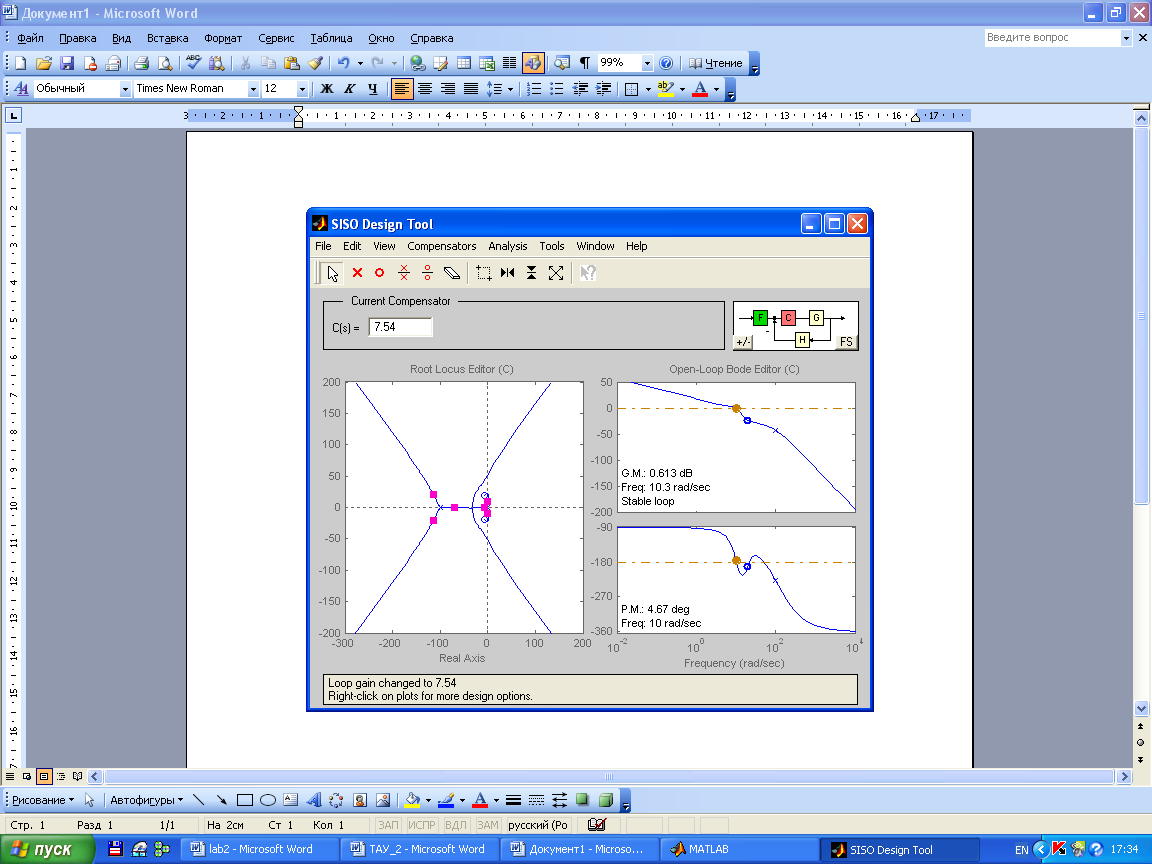
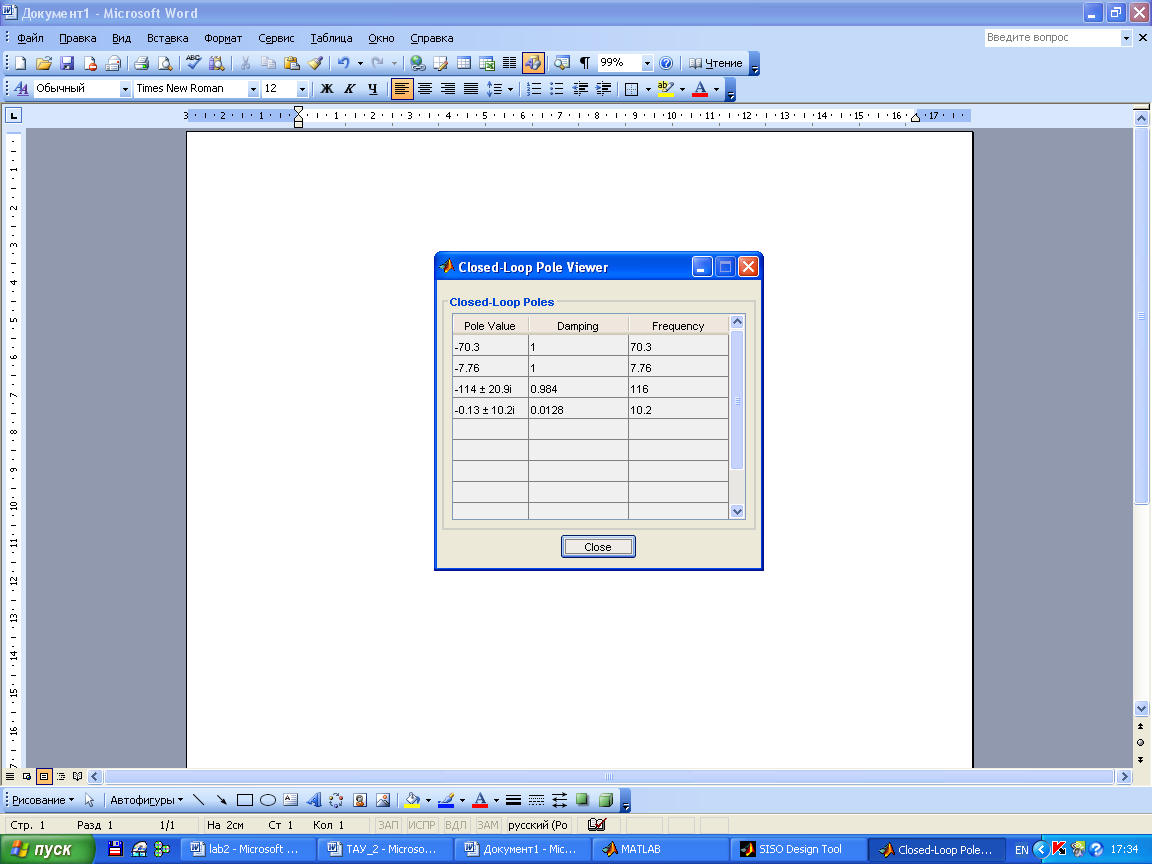
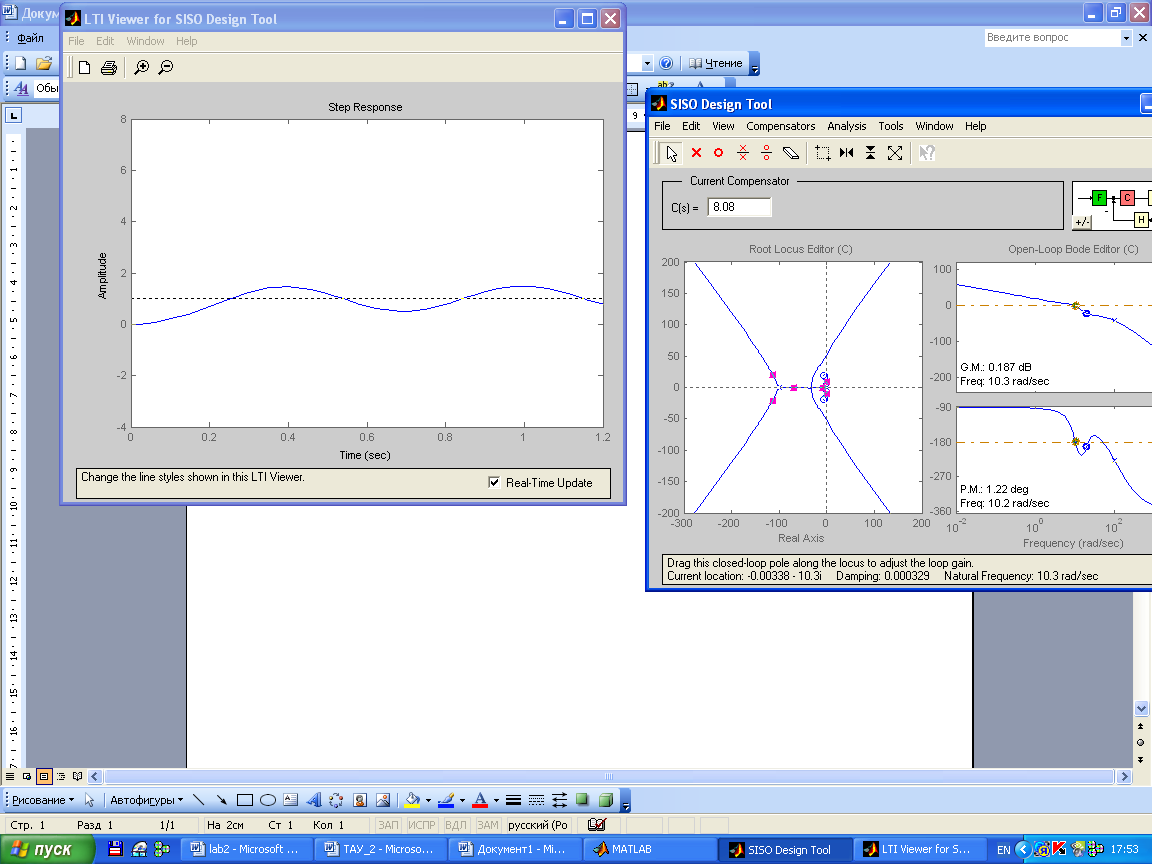
Рассмотрим систему в неустойчивом состоянии:

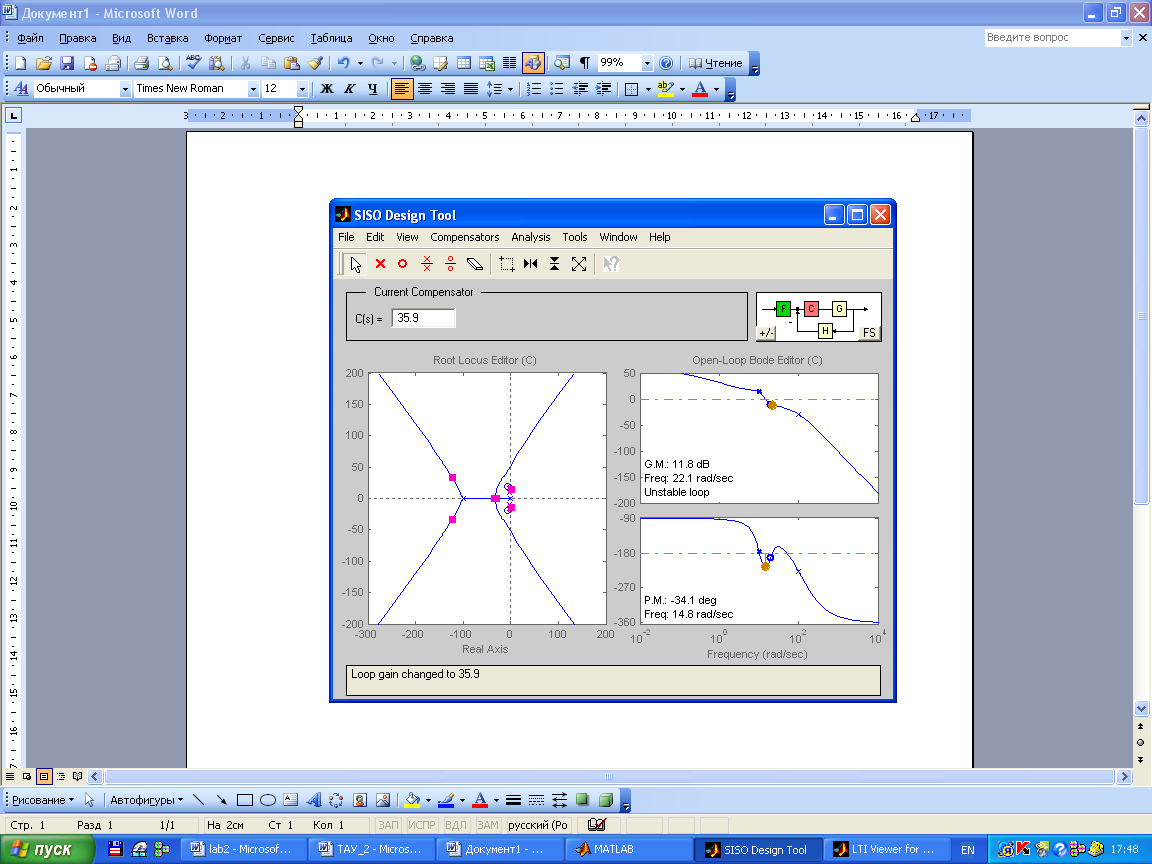
Переходный процесс:

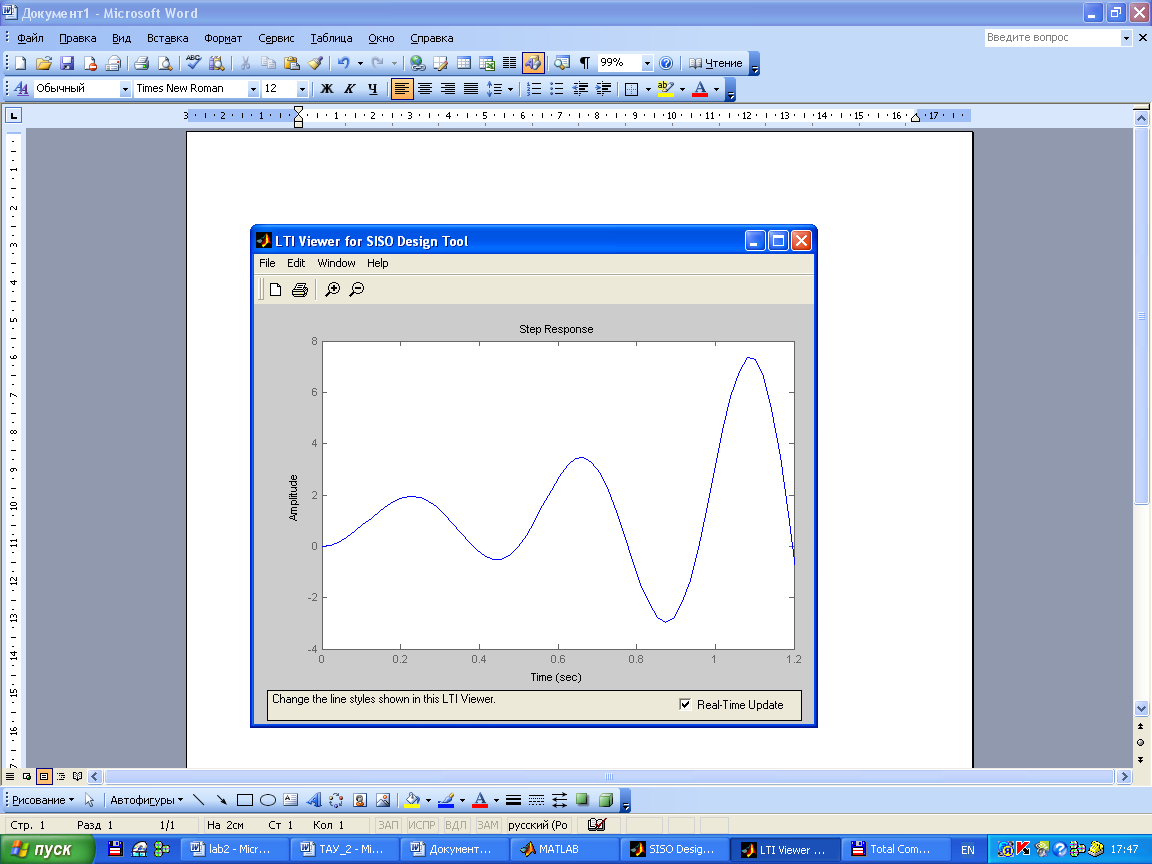
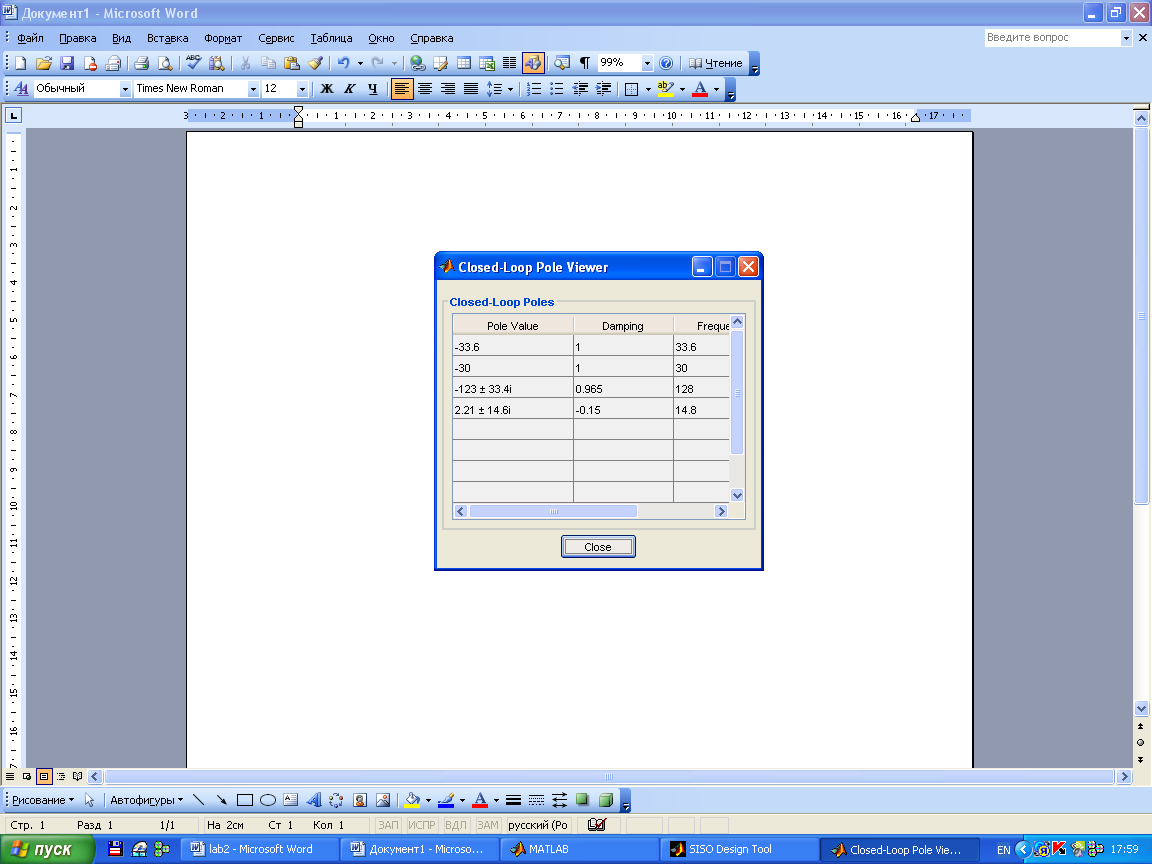
Вывод: проведя данную лабораторную работу, мы знакомились с методикой построения корневых годографов для анализа и синтеза линейных систем автоматического управления в системе Matlab. Данные были получены путем непосредственного взаимодействия на характеристики системы. Такие манипуляции с характеристиками можено сделать в Matlab’е, что выгодно отличает его от MathCad’a.