лабораторная работа / Исследование САУ на устойчивость

Исследование САУ на устойчивость.

1.Схема исследования - последовательное соединение апериодического и колебательного звеньев (разомкнутая САУ):

• Исследование на устойчивость по переходной характеристики:

Переходная характеристика звена:

Вывод: из переходной характеристики видно, что САУ является устойчивой, т.к. система вернулась в равновесное состояние.

• Исследование на устойчивость, используя критерий Михайлова:

Строим АФХ(годограф) САУ (среда Matlab):

1) w=0:0.001:100;//интервал изменения частоты

2) W=4./(-2.304*j.*w.^3 - 6.*w.^2 + j.*w + 1);//задание передаточной ф-ции

3) xlabel('Real axes');ylabel('Image axes');//заголовки осей

4) plot(real(W),imag(W),'R');//вывод АФХ

5) grid on;//отображение сетки

Вывод: САУ является устойчивой, т.к. выполняется критерий Михайлова (необходимое и достаточное условие для устойчивости САУ): годограф проходит три квадранта в соответствии с порядком характеристического уравнения (n=3).

• Исследование на устойчивость, используя критерий Гурвица:

Учитывая последовательное соединение звеньев найдём общую передаточную ф-цию САУ:

Запишем характеристическое уравнение (знаменатель передаточной ф-ции),составим определитель Гурвица и найдём все 3 диагональных минора:

()

()

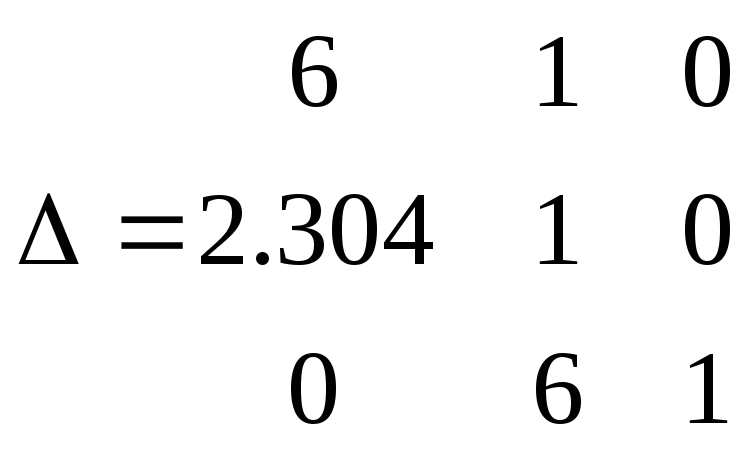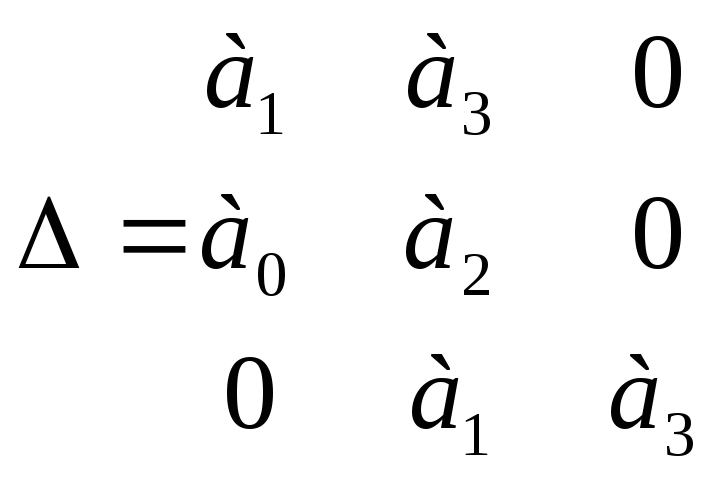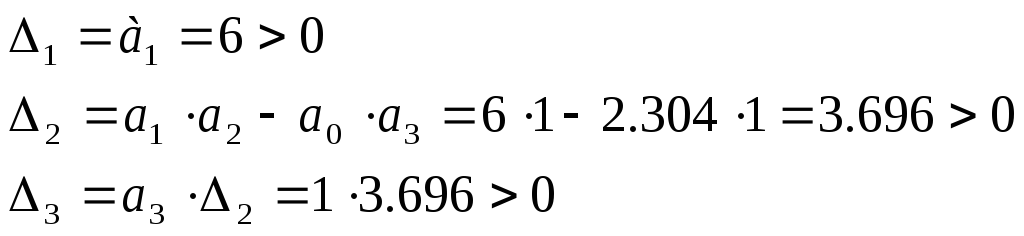
Вывод: САУ является устойчивой, т.к. выполняется критерий Гурвица (необходимое и достаточное условие для устойчивости САУ): все диагональные миноры являются положительными.

Вывод: т.к. выполняются два необходимых и достаточных критерия устойчивости САУисследуемая САУ является устойчивой.

2.Схема исследования - последовательное соединение апериодического и колебательного звеньев с отрицательной обратной связью (замкнутая САУ):

• Исследование на устойчивость по переходной характеристики:

Переходная характеристика звена:

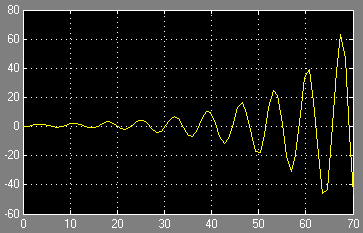
Вывод: из переходной характеристики видно, что САУ является неустойчивой, т.к. система не вернулась в равновесное состояние.

• Исследование на устойчивость, используя критерий Найквиста:

Строим годограф Найквиста (среда Matlab):

1) Wp=tf([4],[2.304 6 1 1]);// задаём передаточную ф-цию разомкнутой системы

Transfer function:

4

-------------------------

2.304 s^3 + 6 s^2 + s + 1

2) nyquist (Wp); //строим годограф Найквиста.

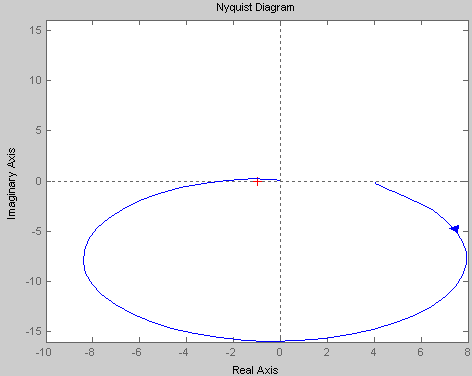
Вывод: т.к. разомкнутая САУ является устойчивой, то по критерию Найквиста для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф разомкнутой системы не охватывал точку (1,0j). В данном случае точка (1,0j) охватывается, т.е не выполняется критерий Найквистазамкнутая САУ- неустойчивая.

Вывод: в ходе лабораторной работы были исследованы на устойчивость две САУ: разомкнутая и замкнутая. Разомкнутая САУ является устойчивой, т.к. выполняются необходимые и достаточные критерии устойчивости (Михайлова, Гурвица). Замкнутая САУ – неустойчивая, т.к. не выполняется необходимый и достаточный критерий устойчивости (критерий Найквиста).