
лабораторная работа / Исследование систем со скользящими режимами (4)
.docСАРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ
ФАКУЛЬТЕТ ИНЖЕНЕРНО - СТРОИТЕЛЬНЫЙ
КАФЕДРА «УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ»
Практическая работа
«Исследование систем со скользящими режимами»
Вариант №14
Выполнил:
ст. гр. УИТ-42
Рязанов И.К.
Принял:
Скоробогатова Т.Н.
2008
Цель работы: Исследовать возможность разделения движений в системе при наличии малых инерционностей и оценить влияние различных параметров как на полное движение, так и на отдельные его составляющие.
Задание:
Структурная схема системы:
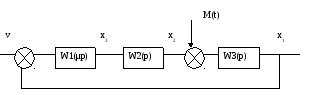

Параметры передаточных функций: K2=6; T2=0,5; d=0.6; K3=2; μ=0,1.
Подставим данные параметры и получим следующие выражения для передаточных функций:
![]()
![]()
![]()
1) Определим общую передаточную функцию для данной системы:
![]()
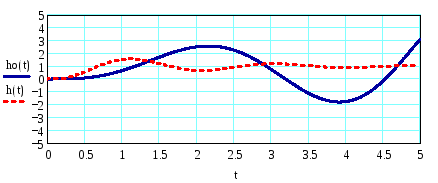
2) Построим график
переходного процесса для данной функции.![]()

Переходный процесс расходящийся, следовательно, данная система не устойчива.
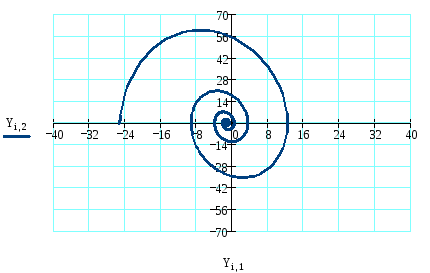
3) Построим фазовый портрет данной системы.

![]()
![]()
![]()

4) Оценим изменение графика переходного процесса при уменьшении µ.
Из графика видно, что при уменьшении µ переходный процесс становится сходящимся и система становится устойчивой.
5) Оценим изменение фазового портрета при уменьшении µ.

Из графика видно, что при уменьшении µ фазовая траектория системы приближается к нулю, значит, исходная система становится устойчивой.
6) Оценим влияние на переходный процесс параметра d. Будем изменять его в диапазоне от 0,1 до 1.
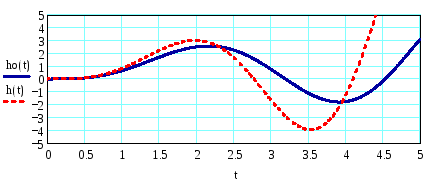
Из графика видно, что процесс остается расходящимся, но амплитуда колебаний увеличивается.
7) Оценим влияние на фазовый портрет параметра d. Будем изменять его в диапазоне от 0,1 до 1.
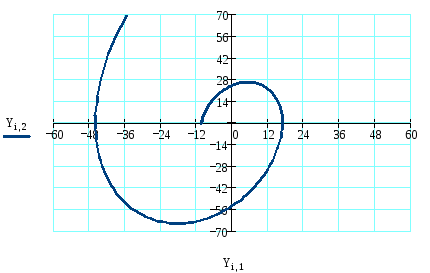
Из графика видно, что при уменьшении параметра d система остается неустойчивой, так как фазовая траектория системы удаляется от начала координат.
8) Оценим влияние на переходный процесс параметра T2 (увеличим Т2 в 3 раза).
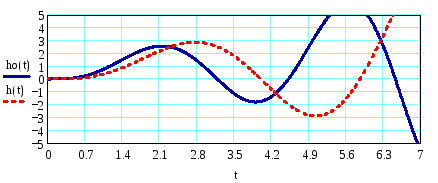
Оба процесса являются расходящимися, но амплитуда колебаний увеличивается.
9) Оценим влияние на фазовый портрет параметра T2 (увеличим Т2 в 3 раза).

Из графика видно, что при увеличении Т2 фазовая траектория системы удаляется от начала координат, значит, система остается неустойчивой.
10) Оценим влияние на переходный процесс параметра К2(увеличим К2 в 2 раза)
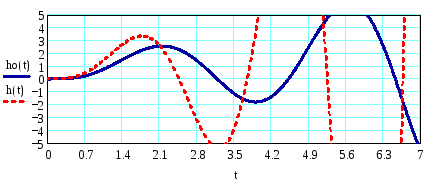
На графике видно, что при увеличении К2 переходный процесс остается расходящимся, но амплитуда колебаний увеличивается.
11) Оценим влияние на фазовый портрет параметра К2(увеличим К2 в 2 раза).
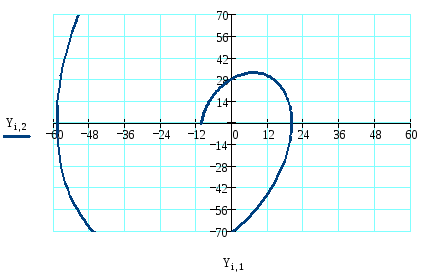
Из графика видно, что при увеличении К2 фазовая траектория системы удаляется от начала координат, значит, система остается неустойчивой.
12) Для того, чтобы оценить возможность разделения движений в системе, исследуем ее корневой портрет. На практике достаточно разнесение корней на порядок.
![]()

![]()
![]()
![]()
![]()
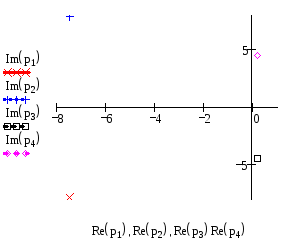
По корневому портрету видно, что в данной системе можно выделить только подсистему медленных составляющих.

ПМД: при µ=0 W1(p)=1 и тогда

Вывод: В ходе выполнения практической работы была исследована возможность разделения движений в системе, которая показала, что в данной системе можно выделить только подсистему медленных движений. Также было оценено влияние всех параметров на работу системы.
