
лабораторная работа / Lab1_var2
.docМинистерство Образования Российской Федерации
Уфимский Государственный Авиационный Технический Университет
Кафедра ТК
Отчет по лабораторной работе №1
по предмету «Основы теории управления»
на тему: Исследование характеристик типовых динамических звеньев
Вариант №2
Выполнил:
Проверил:
Уфа 2005
1. Цель работы
Целью работы является изучение временных и частотных характеристик типовых динамических звеньев с использованием автоматизированных средств моделирования на ПК – MATLAB.
2. Выполнение работы
Таблица
|
№ |
Апериод звено |
Апериодич. звено 2 пор. (колеб. звено) |
Интегр звено |
Изодр. звено |
Реальное диф. звено |
Инерц.-форс Звено |
|||||||
|
K |
T [с] |
K |
T [с] |
ξ |
K |
K1 |
K2 |
K |
τ [с] |
K |
T0 [с] |
T [с] |
|
|
2 |
3 |
0,3 |
2 |
0,3 |
1,5 (0,15) |
3 |
3 |
1 |
3 |
0,3 |
3 |
3 |
1,2 |
2.1. Позиционные звенья
2.1.1. Апериодическое (инерционное) звено первого порядка
Передаточная функция данного
звена имеет вид
![]() .
.
Временные характеристики
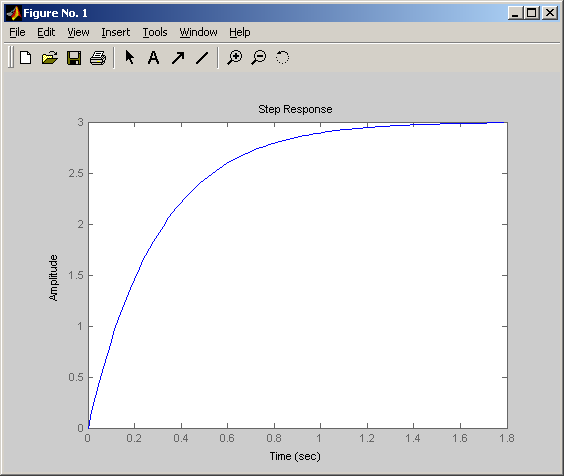
Переходная – получаемая с помощью функции step в MATLAB:
Переходная функция имеет
вид
![]() .
.
Постоянная времени T переходной функции h(t) определяет наклон касательной в начале кривой, т.е. величина T характеризует степень инерционности динамического звена.
Переходная
Весовая (импульсная переходная) - получаемая с помощью функции impulse в MATLAB:
Весовая

Частотные характеристики
Логарифмическая амплитудная и фазовая частотные характеристики – выполняемые в MATLAB с помощью функции bode:
Логарифмическая амплитудная и фазовая частотные характеристики
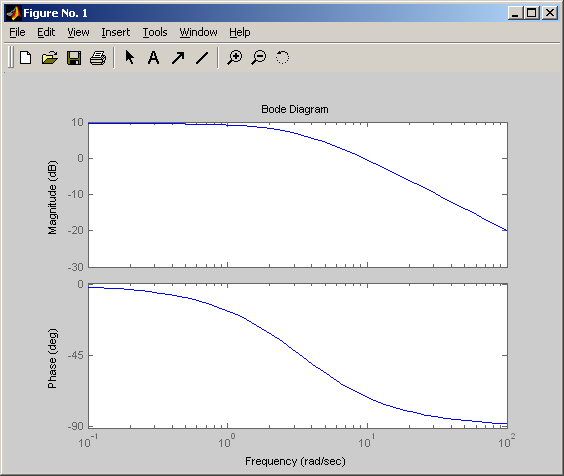
Амплитудно-фазовая частотная характеристика – получаемая в MATLAB с помощью функции nyquist:
Амплитудно-фазовая характеристика звена имеет вид:
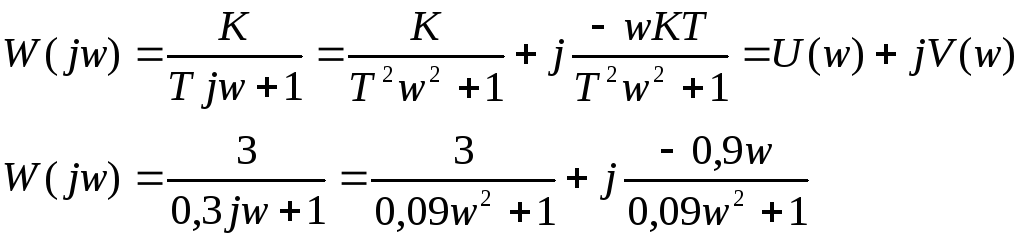
Амплитудно-фазовая частотная характеристика

 Im
Im

 K
K




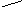

 Re
Re
w=∞ w=0

 A
A
w
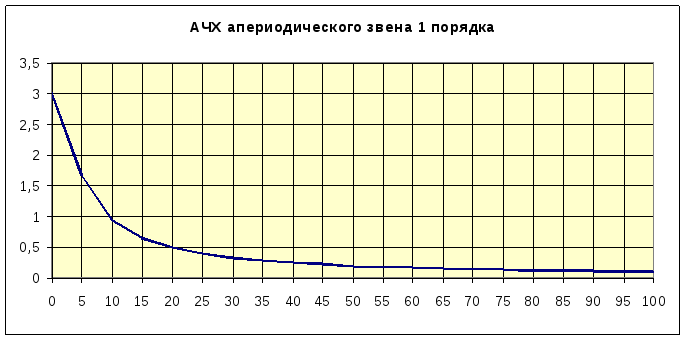
Амплитудно-частотная характеристика имеет вид:
![]()
Фазо-частотная характеристика имеет вид:
![]()

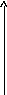
 A
w=1/T
A
w=1/T




 K w,
с-1
K w,
с-1
![]()





 w, с-1
w, с-1 ![]()
 0 w=1/T
0 w=1/T ![]()
2.1.2. Апериодическое звено второго порядка
Передаточная функция звена имеет вид
![]()
![]()
где
![]() - коэффициент затухания.
- коэффициент затухания.
Эта передаточная функция может быть записана также в виде
![]()
где T1
и T2
соответствующие постоянные времени,
определяемые корнями характеристического
уравнения
![]()
Определение корней характеристического уравнения
![]()
![]()
![]()
Временные характеристики
Переходная

Весовая (импульсная переходная)
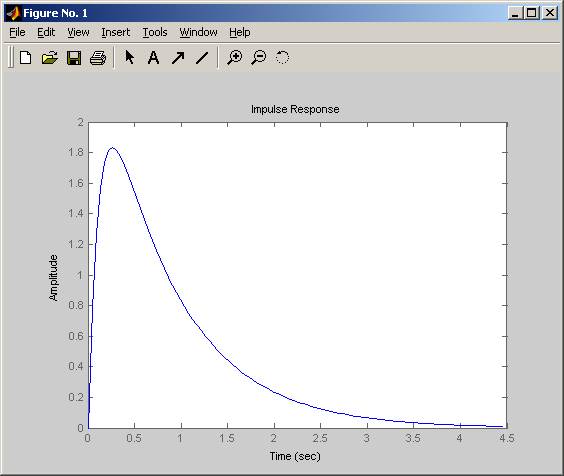
Частотные характеристики
Логарифмическая амплитудная и фазовая частотные характеристики
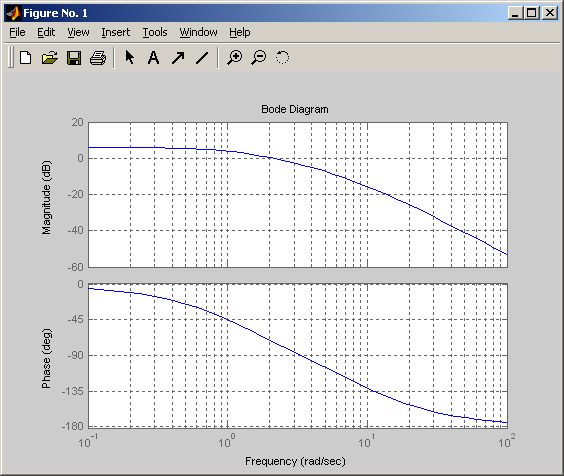
Амплитудно-фазовая частотная характеристика

Im
 K
K
 w=∞ w=0 Re
w=∞ w=0 Re




 A
A
![]() w
w
Амплитудно-частотная характеристика имеет вид
![]()
![]()
![]()
![]()
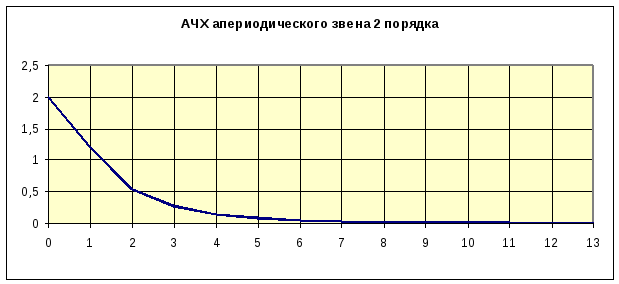
Фазо-частотная характеристика имеет вид
![]()
![]()


A 

![]()
 w w
w w





 o 0
o 0
![]()
![]()
![]()
Асимптотическая ЛАХ приведена на рис. 1






 L(w)
-20 дб/дек
L(w)
-20 дб/дек
20lgK
 -40
дб/дек
-40
дб/дек
0 w1 w2 wср lgw
Рис. 1
![]()
![]()
![]()
![]()
![]()
2.1.3. Колебательное звено второго порядка
Передаточная функция имеет вид
![]() (1)
(1)
![]()
Величина
![]() в (1) представляет частоту собственных
колебаний.
в (1) представляет частоту собственных
колебаний.
Временные характеристики
Переходная
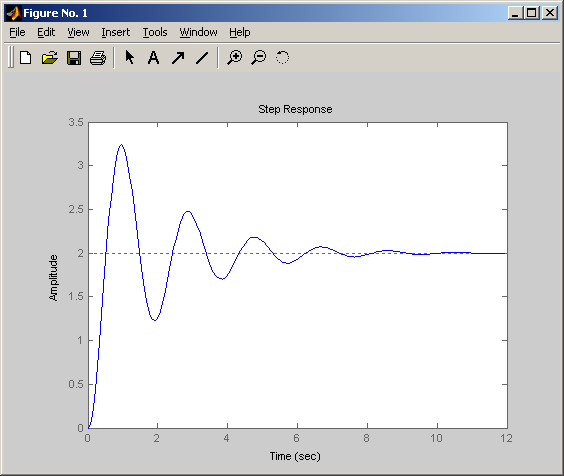
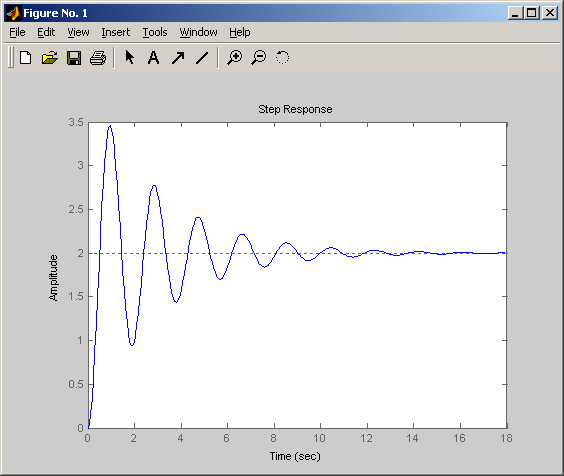
![]()
![]()
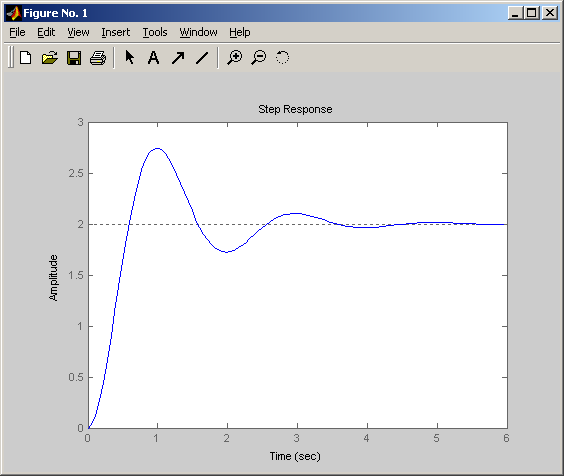
![]()
Снижение параметра затухания ξ приводит к повышению колебательности переходного процесса.
Весовая (импульсная переходная)
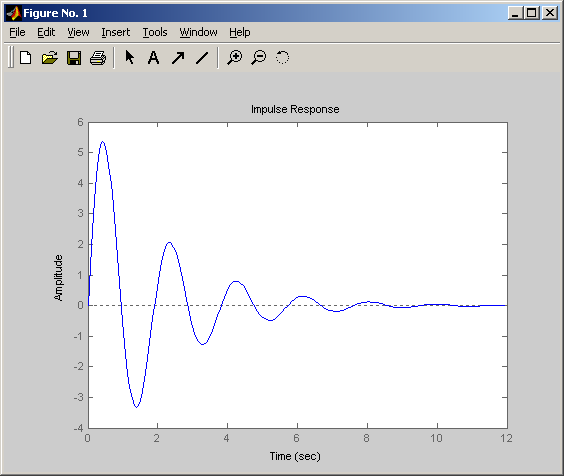
Частотные характеристики
Логарифмическая амплитудная и фазовая частотные характеристики
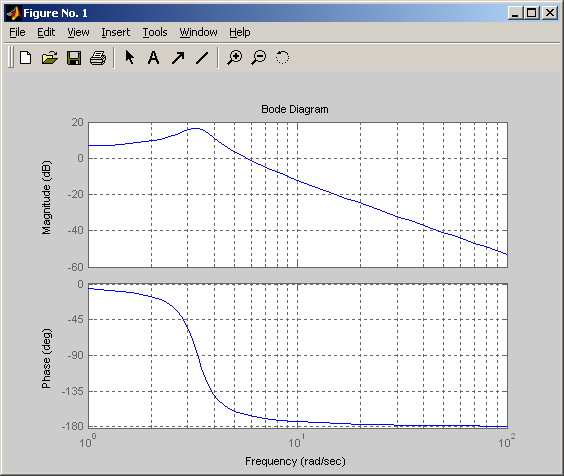
ЛАХ и ФЧХ при ξ=0,15

ЛАХ и ФЧХ при ξ=0,1

ЛАХ и ФЧХ при ξ=0,4
Снижение параметра затухания ξ приводит к росту резонансного пика ЛАХ.
Чем больше параметр ξ , тем более пологий будет график ЛФХ.
При ξ=0 звено – консервативное,
графики АЧХ и ЛАХ будут иметь разрыв
на частоте
![]() ;
а график ЛФХ будет иметь вид прямых
линий.
;
а график ЛФХ будет иметь вид прямых
линий.






 L(w), дб
L(w), дб ![]()
![]()
![]() w
w


 w0
w0 




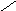




![]()
![]()
![]()
![]()
![]()


 K
K



![]()
![]()
lgw, дек
0 w0
Амплитудно-фазовая частотная характеристика колебательного звена имеет вид:
![]()
![]()
Амплитудно-фазовая частотная
характеристика
 Im
Im
K



 w=∞
w=0 Re
w=∞
w=0 Re

![]()
 A
w
A
w
![]()
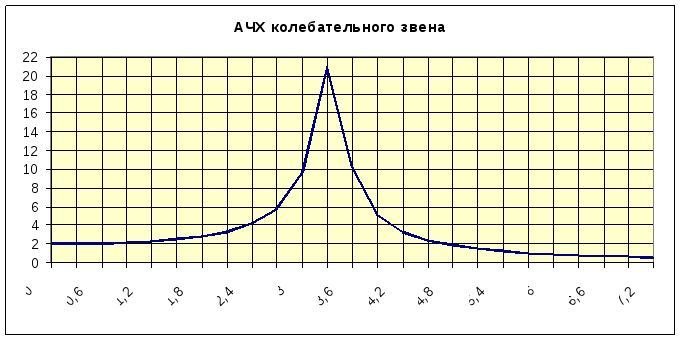
АЧХ может иметь резонансный
пик. Исследование модуля частотной
передаточной функции на максимум
показывает, что пик будет существовать
при ξ<0,578. Высота пика будет тем больше,
чем меньше параметр затухания:
![]()
Максимуму АЧХ соответствует
частота
![]()
АЧХ колебательного звена описывается выражением:
![]()
![]()
Фазо-частотная характеристика колебательного звена описывается выражением:
![]()
![]()

2.2. Интегрирующие звенья
2.2.1. Идеальное интегрирующее звено
Данное звено имеет передаточную функцию
![]()
![]()
Временные характеристики
Переходная функция идеального интегрирующего звена
![]()
![]()
Переходная

Весовая (импульсная переходная)
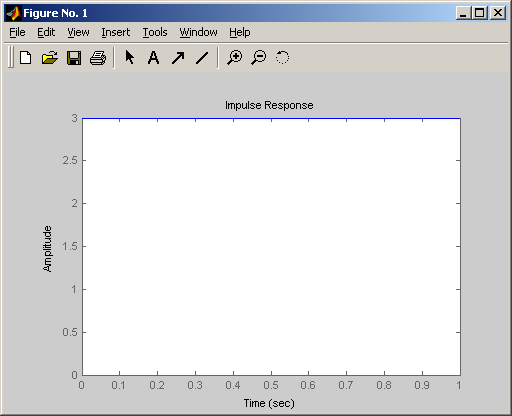
Частотные характеристики
Логарифмическая амплитудная и фазовая частотные характеристики
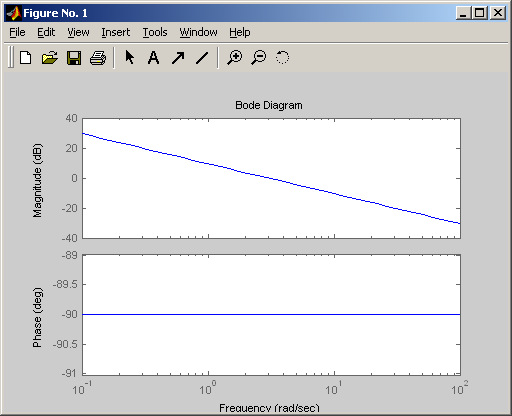
Амплитудно-фазовая частотная характеристика имеет вид:
![]()
Амплитудно-фазовая частотная характеристика

АЧХ интегрирующего звена описывается выражением:
![]()
![]()

ФЧХ интегрирующего звена описывается выражением:
![]()

2.2.2. Изодромное звено (пропорционально-интегрирующее звено)
Это звено имеет передаточную функцию
![]()
![]()
т.е. его можно представить как параллельное соединение интегрирующего и пропорционального (безынерционного) звеньев. После простых преобразований это звено можно также записать в виде:
![]()
![]() (2)
(2)
где (1+τs) - форсирующее звено, τ =K2/K1.
Таким образом, в соответствии с (2) изодромное звено может быть также представлено как последовательное соединение интегрирующего и форсиру-ющего звеньев.
Временные характеристики
Переходная функция пропорционально-интегрирующего звена
![]()
![]()
Переходная
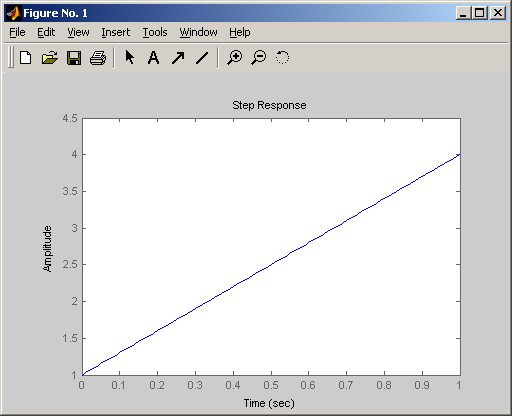
Весовая (импульсная переходная)
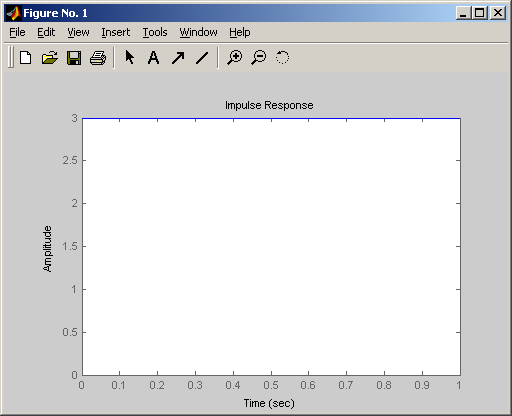
Частотные характеристики
Логарифмическая амплитудная и фазовая частотные характеристики
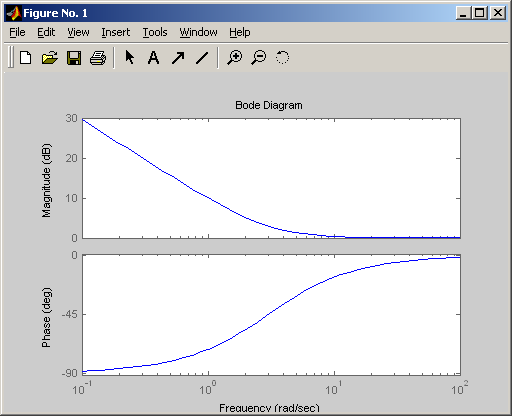
Амплитудно-фазовая частотная характеристика
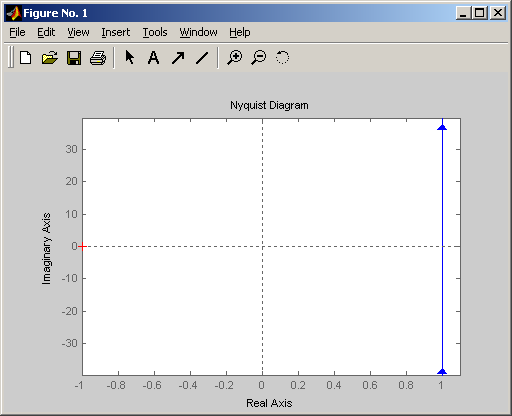
Поскольку изодромное звено может быть также представлено как последователь-ное соединение интегрирующего и форсирующего звеньев, АЧХ изодромного звена описывается выражением:
![]()
![]()
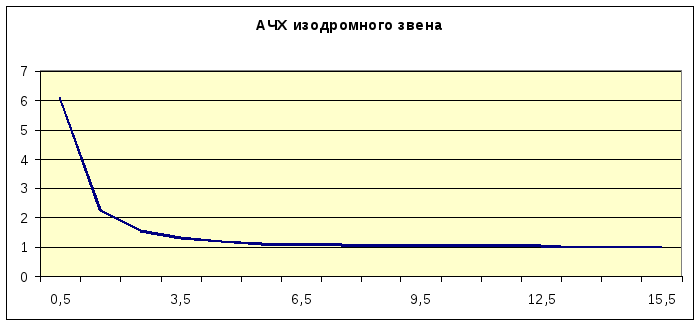
ФЧХ изодромного звена описывается выражением:
![]()
![]()

2.3. Дифференцирующие звенья
2.3.1. Реальное дифференцирующее звено
Передаточная функция звена
![]() ,
,
![]()
Временные характеристики
Переходная функция звена имеет вид
![]()
![]()
Переходная

Весовая (импульсная переходная)

Частотные характеристики
Логарифмическая амплитудная и фазовая частотные характеристики
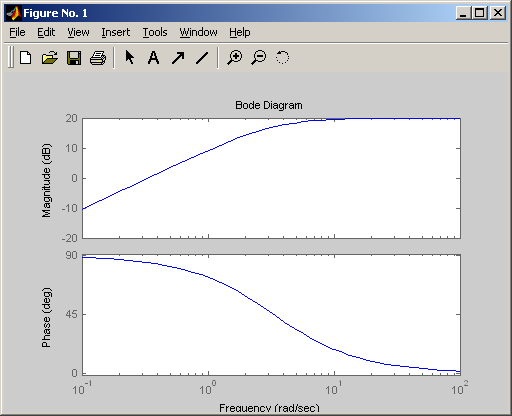
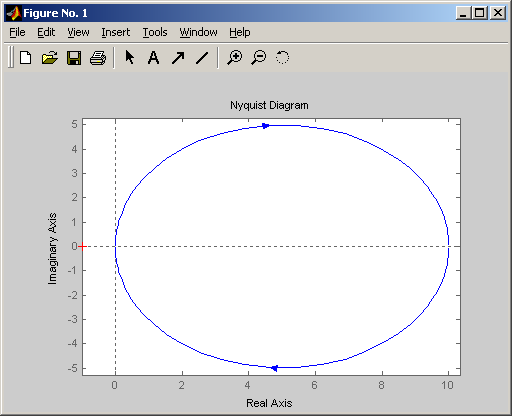
Амплитудно-фазовая частотная характеристика дифференцирующего звена равна:
![]()
![]()
Амплитудно-фазовая частотная характеристика
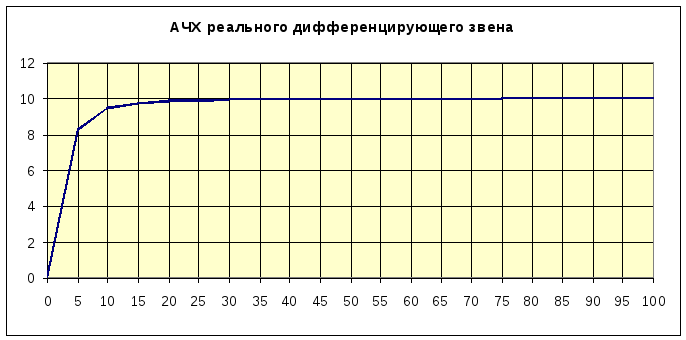
АЧХ реального дифференцирующего звена равна:
![]()
![]()
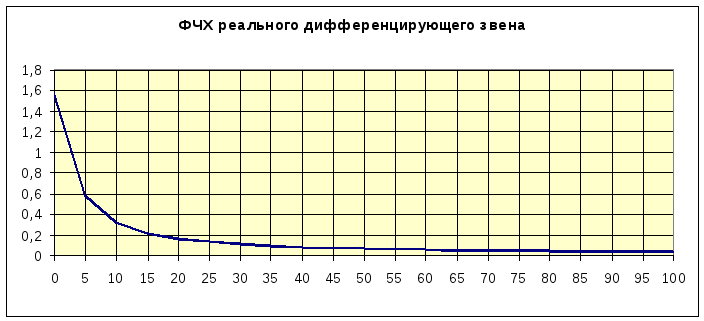
ФЧХ равна:
![]()
![]()
2.3.2. Инерционно-форсирующее (реальное форсирующее) звено
Передаточная функция звена
![]() (3)
(3)
![]()
В установившемся режиме выходная величина данного звена пропорциональна входной, т.е. оно может быть отнесено к звеньям позиционного типа.
При η >> 1 оно по своим свойствам приближается к форсирующему звену.
Таким образом, в соответствии с (3) инерционно-форсирующее звено может быть также представлено как последовательное соединение инерционного и форсиру-ющего звеньев.
Временные характеристики
Переходная


h(t)



K(T0 /T)


 T
T
