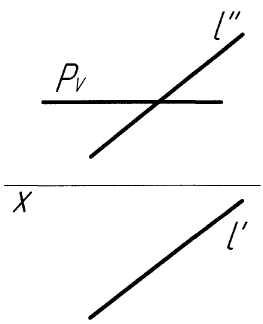1.3. Основные теоретические положения

Пересечение прямой линии с плоскостью. Для построения точки пересечения прямой с плоскостью необходимо выполнить следующее (рис. 2):

1) через заданную прямую провести вспомогательную плоскость, перпендикулярную одной из плоскостей проекций;

2) построить линию пересечения заданной и вспомогательной плоскостей;

3) определить искомую точку пересечения прямой с плоскостью как точку пересечения заданной прямой и построенной линии пересечения плоскостей.

Рис. 2

Если объекты проецирования занимают относительно плоскостей проекций частное положение, то решение задачи упрощается.

Пример 1. Построить точку пересечения прямой l с плоскостью Р, заданной следами и перпендикулярной горизонтальной плоскости проекций (рис. 3, а).

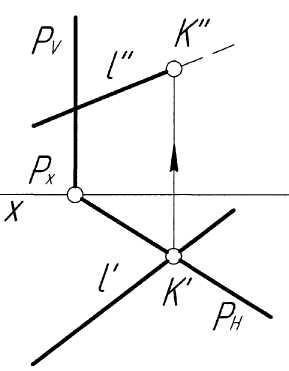
Решение. Поскольку плоскость Р (Р_Н, Р_V) является горизонтально-проецирующей, то проекция K' точки пересечения прямой с плоскостью должна принадлежать одновременно и проекции l' и следу Р_Н (рис. 3, б). По проекции K' точки пересечения строим ее проекцию K'', исходя из условия принадлежности точки K прямой l. В заключение определяем видимость элементов чертежа методом конкурирующих точек, описание которого приведено ниже.

Пример 2. Построить точку пересечения прямой l с плоскостью Р, заданной следами и параллельной горизонтальной плоскости проекций (рис. 4, а).

Решение. Решение задачи аналогично примеру 1. Проекцию K'' точки пересечения прямой с плоскостью определяем как точку пересечения следа Р_V с проекцией l'' (рис. 4, б). По проекции K'' строим проекцию K' искомой точки, исходя из условия принадлежности ее прямой l. В заключение определяем видимость элементов чертежа.

а)	б)
Рис. 3

а)	б)
Рис. 4

а)	б)
Рис. 5

Пример 3. Построить точку пересечения прямой l с плоскостью Р общего положения (рис. 5, а).

Решение. Решение задачи производим в следующей последовательности (рис. 5, б). Заключаем прямую l (l', l'') в горизонтально-проецирующую плоскость Q (Q_H, Q_V), задав ее следами. Строим точки M (M', M'') и N (N', N''), принадлежащие одновременно обеим плоскостям, и соединяем их прямой MN (M'N', M''N''), которая является линией пересечения плоскости Р (Р_Н, Р_V) с плоскостью Q (Q_H, Q_V). На фронтальной плоскости проекций прямая M''N'' пересекается с прямой l'' в точке K''. Далее строим проекцию K' искомой точки. Определяем видимость элементов чертежа.

Пример 4. Построить точку пересечения прямой l с плоскостью треугольника АВС общего положения (рис. 6, а).

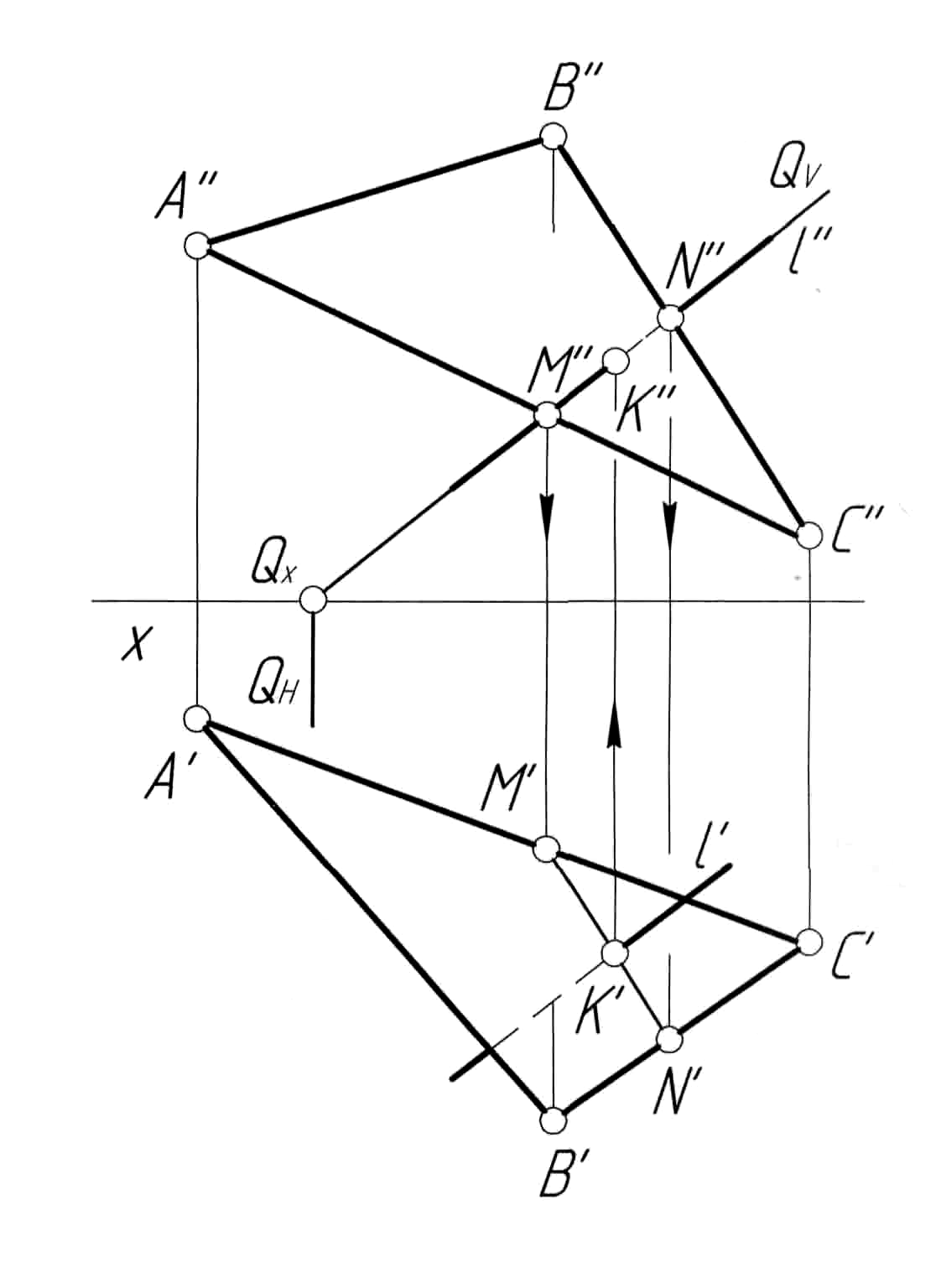
Решение. Решение задачи (рис. 6, б) проводим в последовательности, аналогичной примеру 3. Заключаем прямую l (l', l'') во фронтально-проецирующую плоскость Q (Q_H, Q_V). Строим точки M (M', M'') и N (N', N''), принадлежащие одновременно обеим плоскостям, и соединяем их прямой MN (M'N', M''N''), которая является линией пересечения плоскости треугольника АВС с плоскостью Q. На горизонтальной проекции прямая M'N' пересекается с прямой l' в точке K'. Далее строим проекцию K'' искомой точки. Определяем видимость элементов чертежа.

а)	б)
Рис. 6

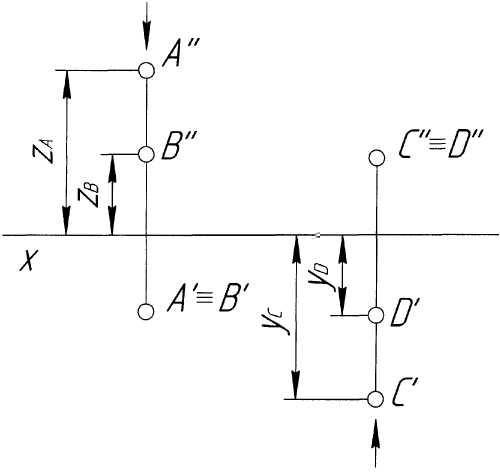
Определение видимости элементов чертежа. При решении задач на пересечение геометрических объектов, когда на эпюре их изображения накладываются друг на друга, возникает необходимость в определении взаимной видимости элементов чертежа, поскольку считается, что проецируемые плоскости и поверхности непрозрачны. Видимость элементов чертежа определяется методом конкурирующих точек. Конкурирующими называются такие точки пространства, у которых одноименные проекции на одной из плоскостей проекций совпадают. На рис. 7 показаны две пары конкурирующих точек А и В (совпадают их горизонтальные проекции) и C и D (совпадают их фронтальные проекции).

Рис. 7	Рис. 8

Метод конкурирующих точек состоит в определении взаимной видимости точек по их несовпадающим проекциям. Считается, что наблюдатель смотрит на плоскости проекций из бесконечности, а его луч зрения параллелен проецирующему лучу. Поэтому точка А (рис. 7), находящаяся выше точки В (z_A > z_B), расположена ближе к наблюдателю и на горизонтальной проекции закрывает точку В.

На фронтальной проекции видна точка С, поскольку она находится дальше от фронтальной плоскости проекции (y_С > y_D) или, что то же самое, дальше от оси проекций х на горизонтальной проекции, и закрывает невидимую точку D.

Пользуясь этим методом (рис. 8), можно определить, что прямая m находится перед прямой n, так как точка 1, принадлежащая прямой m, расположена перед точкой 2, находящейся на прямой n (y₁ > y₂).

Таким образом, элементы чертежа (точки, линии, участки плоскостей и поверхностей), которые расположены между плоскостью проекций и наиболее удаленным от плоскости проекций объектом проецирования, являются невидимыми для наблюдателя. При этом объекты проецирования должны быть расположены между наблюдателем и плоскостью проекций.

а)	б)
в)	г)
Рис. 9

Рассмотрим определение видимости элементов в примере 1 (рис. 3, б и 9, а). В качестве конкурирующих возьмем точки 1 (1', 1'') и 2 (2', 2'') на двух скрещивающихся прямых: фронтальном следе Р_V и прямой l соответственно. На фронтальной плоскости проекций эти точки совпадают, находим их горизонтальные проекции. Так как проекция 2' расположена дальше от оси проекций, то точка 2 считается видимой. Следовательно, для наблюдателя на фронтальной плоскости проекций видимой будет та часть прямой l, которая расположена левее точки пересечения. На горизонтальной проекции вся проекция прямой l видима.

Видимость элементов чертежа в примере 2 (рис. 4, б и 9, б) определяется аналогично. В качестве скрещивающихся прямых взяты след Р_V и прямая l. В видимости конкурируют две точки 1 и 2, причем точка 1 (1', 1'') принадлежит плоскости Р, а точка 2 (2', 2'') – прямой l. На горизонтальной проекции эти точки совпадают, находим их фронтальные проекции. Так как точка 1'' расположена дальше от оси проекций, чем 2'', то точка 1 считается видимой. Следовательно, для наблюдателя на горизонтальной плоскости проекций часть прямой правее точки пересечения будет видимой, а левее точки пересечения – невидимой.

На рис. 9, в, г показаны примеры определения видимости прямой l, пересекающейся с плоскостями общего положения Р (см. пример 3, рис. 5, б) и треугольника АВС (см. пример 4, рис. 6, б).

Перпендикулярность прямой и плоскости. Прямая перпендикулярна

плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим

Рис. 10

в этой плоскости (рис. 10). В качестве таких двух пересекающихся прямых целесообразно выбирать горизонталь и фронталь плоскости, поскольку в этом случае образуются прямые углы, одна из сторон которых параллельна соответствующей плоскости проекций, а следовательно, по правилу проецирования плоского прямого угла эти прямые углы будут проецироваться на плоскости проекций без искажения. Таким образом, на эпюре фронтальную проекцию перпендикуляра проводят перпендикулярно фронтальной проекции фронтали, а горизонтальную проекцию – перпендикулярно горизонтальной проекции горизонтали. В том случае, если на эпюре плоскость задана следами, то проекции прямой, перпендикулярной плоскости, должны быть перпендикулярны к одноименным следам плоскости.

Пример 5. Определить расстояние от точки D до плоскости Р, заданной следами (рис. 11, а).

а)	б)
Рис. 11

Решение. Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опущенного из точки на заданную плоскость. Поэтому решение задачи производим в следующей последовательности (рис. 11, б):

1) из точки D опускаем на плоскость Р перпендикуляр l. Для этого через точку D'' проводим прямую l'' перпендикулярно следу P_V, а через точку D' проводим прямую l' перпендикулярно следу P_Н ;

2) определяем точку K (K', K'') основания перпендикуляра как точку пересечения прямой l с плоскостью Р (см. пример 3);

3) определяем натуральную величину отрезка перпендикуляра DK (D'K', D''K'') методом прямоугольного треугольника как гипотенузу прямоугольного треугольника, одним из катетов которого является проекция отрезка на плоскость проекций (например, D''K''), а другим – разность расстояний от концов отрезка до той же плоскости проекций (в нашем примере – y).

Построенный отрезок D₀K'' и определяет расстояние от точки D до плоскости Р.

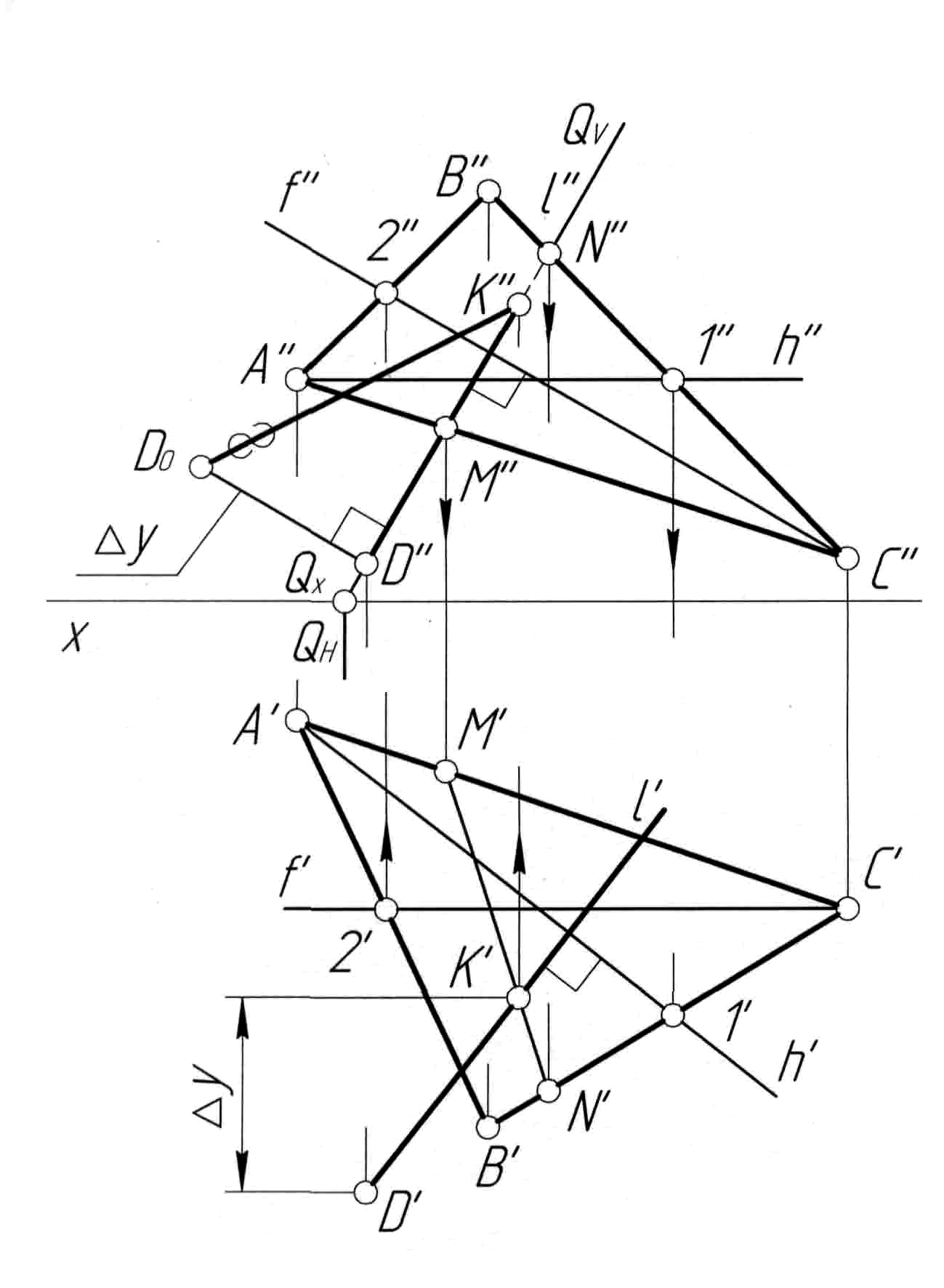
Пример 6. Определить расстояние от точки D до плоскости, заданной треугольником ABC (рис. 12, а).

Решение. Решение задачи (рис. 12, б) проводим в последовательности, аналогичной примеру 5. Для построения перпендикуляра l, опущенного из точки D на плоскость треугольника ABC, в плоскости проводим горизонталь h (h', h'') и фронталь f (f', f''). Далее через точку D'' проводим прямую l'' перпендикулярно f'', а через точку D' строим прямую l' перпендикулярно h'. Затем строим точку K пересечения прямой l с плоскостью треугольника ABC (см. пример 4) и находим натуральную величину отрезка DK (D'K', D''K'') методом прямоугольного треугольника (см. пример 5).

а)	б)
Рис. 12

Параллельность прямой и плоскости. Если прямая параллельна прямой, лежащей в заданной плоскости, то она параллельна и самой плоскости. Для того чтобы проверить, параллельна ли прямая заданной плоскости, можно поступить одним из двух следующих способов:

1) в плоскости проводят прямую, параллельную заданной. Если такую прямую в плоскости подобрать не удается, значит прямая и плоскость не параллельны;

2) строят точку пересечения заданной прямой с плоскостью. Если такая точка не может быть найдена, то прямая и плоскость параллельны.

Пример 7. Провести через точку K прямую, параллельную плоскости, заданной треугольником ABC (рис. 13, а).

Решение. Для того чтобы построить прямую, проходящую через заданную точку параллельно заданной плоскости, необходимо провести через эту точку прямую, параллельную какой-либо прямой, принадлежащей плоскости треугольника. Известно, что таких прямых может быть бесчисленное множество. На рис. 13, б прямая l параллельна стороне АВ треугольника АВС, и поэтому параллельна плоскости. На рис.13, в прямая l параллельна горизонтали h плоскости треугольника АВС и поэтому также параллельна заданной плоскости.

а)	б)	в)
Рис. 13

Параллельность плоскостей. Две плоскости считаются параллельными, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Одноименные следы параллельных плоскостей между собой параллельны.

Пример 8. Построить плоскость, заданную двумя пересекающимися прямыми m и n (отсеком), параллельную плоскости треугольника ABC и отстоящую от нее на расстоянии 40 мм (рис. 14, а).

Решение. Через любую точку в плоскости треугольника АВС, например, вершину С (C', C''), проводим прямую, перпендикулярную этой плоскости. Для этого строим в плоскости АВС горизонталь h (h', h'') и фронталь f (f', f''). Далее через точку С'' перпендикулярно f'' проводим проекцию l'', а через С' перпендикулярно h' проводим l'. Выбираем на прямой l произвольную точку Т (Т', Т'') и определяем натуральную величину отрезка CТ (С'Т', С''Т''), вдоль которой от точки С откладываем 40 мм и получаем точку K. Находим проекции точки K (K', K'') на прямой l (l', l''). Далее через точку K (K', K'') проводим две пересекающиеся прямые m (m', m'') и n (n', n''), параллельные двум пересекающимся прямым плоскости треугольника ABC (см. пример 7), например, AB (A'B', A''B'') и BC (B'C', B''C'') соответственно (рис. 14, б). Эти прямые и задают искомую плоскость.

а)	б)
Рис. 14