лабораторная работа / laba2_TAU

Санкт-Петербургский государственный электротехнический

Университет «ЛЭТИ»

кафедра АПУ

Лабораторная работа № 2

Фазовые портреты нелинейных систем

Выполнил: студент группы 5321. Проверил: Проф.ИмаевД.Х

Санкт-Петербург

2008г

Целью работы является исследование фазовых портретов нелинейных систем с помощью программных средств.

1. Осциллятор Вандер- Поля

Дифференциальное уравнение имеет вид:

Положение равновесия:

Получим:

Линеаризация для малых

Устойчивость положения равновесия.

Характеристический полином:

Условия устойчивости не выполняются.

Корни:

Переходный процесс колебательно-расходящийся.

Для исследования поведения при больших , воспользуемся компьютерным моделированием в среде Simulink.

Математическая модель представлена на рис.1, а на рис.2 представлен фазовый портрет.

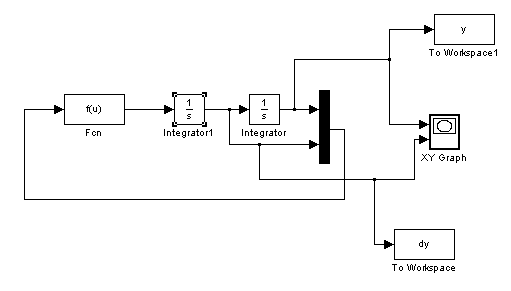
Рис.1.

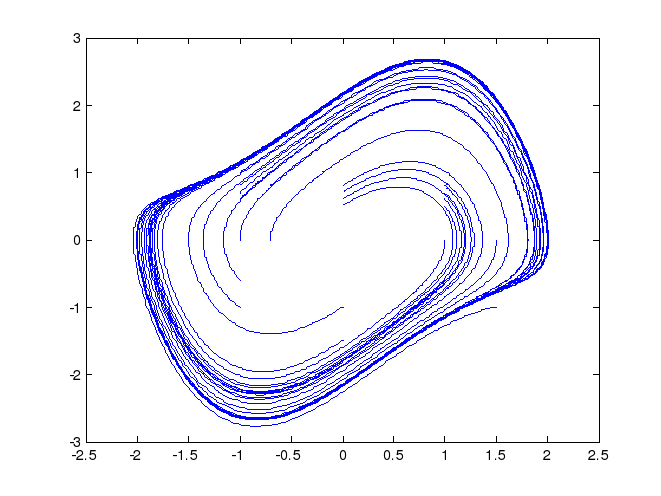
Рис.2. “Неустойчивый фокус.”

2. Математический маятник

Дифференциальное уравнение имеет следующий вид:

где Нелинейность здесь представляет sin.

Положение равновесия:

Рис. 3.

Линеаризация для малых отклонений θ:

«нижние» отклонения

«верхние» отклонения

ХП: корни .

«Центр»

0

Рис. 4.

ХП: корни .

«Седло»

Рис. 5.

Схема в среде Simulink такая же, как изображена на рис. 1. На рис. 6 представлен фазовый портрет.

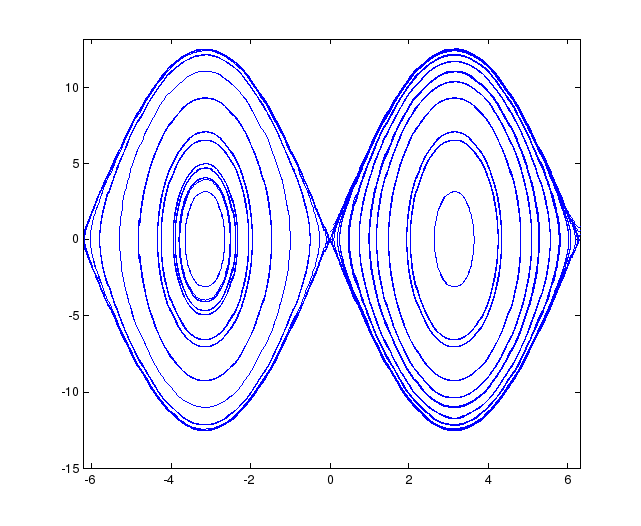
Рис. 6. Естественный базис

3. Релейная система

Математическая модель релейной системы представлена на рис. 7.

g=0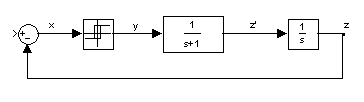

Рис. 7. Математическая модель

Эта система не имеет положения равновесия. Для анализа воспользуемся компьютерным моделированием. Модель системы, построенная в среде Simulink, показана на рис. 8.

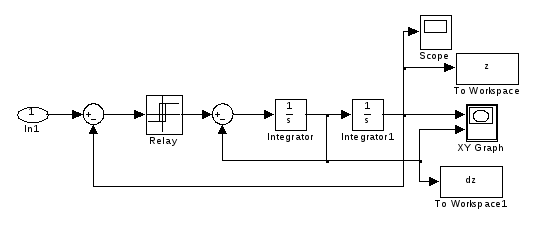
Рис. 8.

Р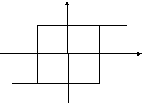еле с гистерезисом:

y

1

-1 1 х

-1

Система совершает колебательные движения. Фазовый портрет представлен на

рис. 9.

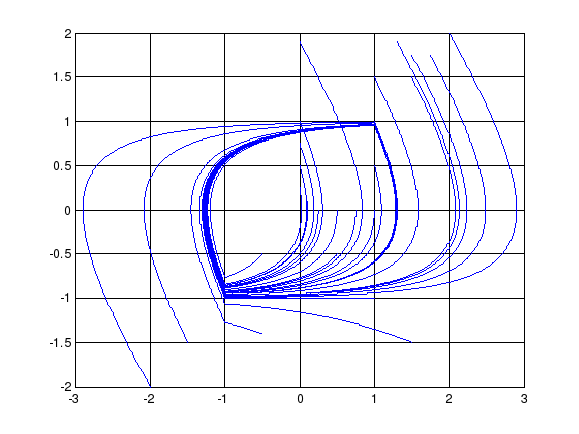
Рис. 9.

6