6. Структурный анализ бмс. Сигнальные графы

БМС представляют собой широкий класс: искусственные органы, системы мониторирования (кардиосигналов) и др.

Биологическое звено:

9. трудная формализуемость

10. сложность и нелинейность описания процессов жизнедеятельности

11. непредсказуемость поведения

12. отсутствие точек входа и выхода

Классическая схема биотехнической системы:

С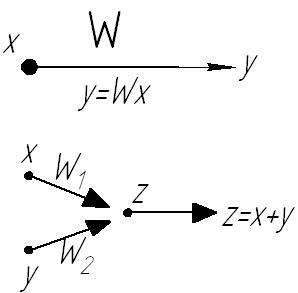игнальный графы находят широкое применение во всех областях науки. Они состоят из совокупности упорядоченных вершин и дуг в форме стрелок. Сигнальный граф отличается от обычного тем, что дугам и вершинам сопоставляется некая величина.

W-передаточная функция в сигнальном графе- это коэффициент передачи. Путь в ориентированном графе - это последовательность вершин и дуг, идущая вдоль стрелок, из некоторой вершины i в вершину j – P(ij), дважды не проходит ни одну вершину. Замкнутый прямой путь называется контуром. Контур всегда означает обратную связь. Общая передача прямого пути равна произведению передач дуг, входящих в этот прямой путь.

Петля – касается прямого пути¸ если у них имеется общая вершина.

Исключение петли:

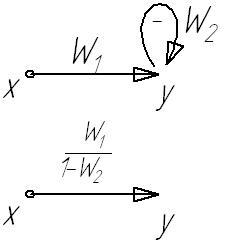
Исключение контура:

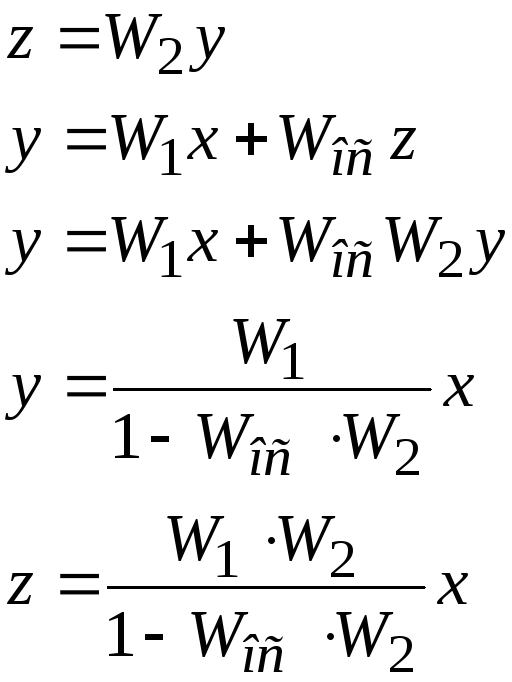
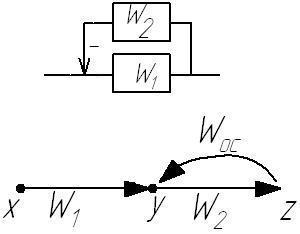
B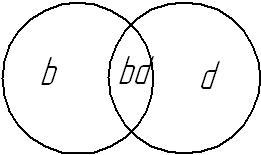d-множество всех коэффициентов петель пересекаются.

Объединение множеств

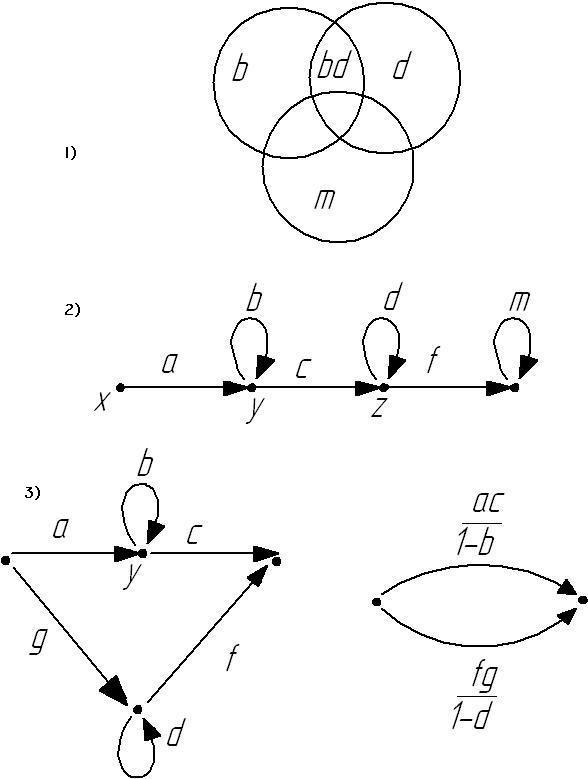
1)b+d+m-bd-dm-bm+bdm

2)

3)

7. Устойчивость линейных систем

Линейная система

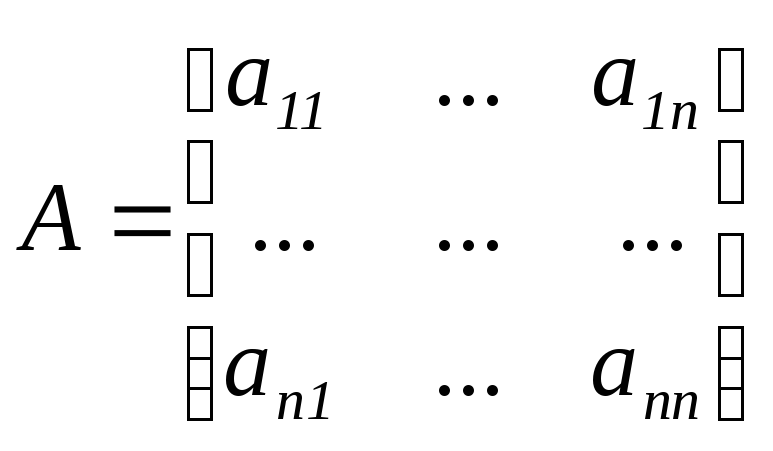
det(A)=0, - корни

можно записать:

Для устойчивости необходимо, чтобы (действительная часть )

Для устойчивости линейной однородной системы необходимо и достаточно, чтобы корни характеристического уравнения имели неположительные вещественные части

Критерий Гаусса-Гурвица

Строится определитель Гурвица

Необходимо, чтобы он имел главный определитель. Если они все будут >0, то такая система будет устойчива

8. Динамические системы

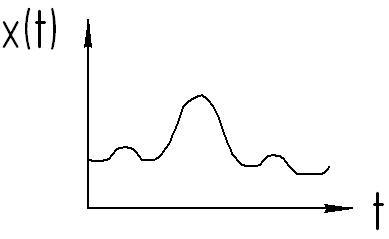
системы, состояние которых изменяется во времени.

Дин. сист. меняют свое состояние посредством переходных процессов.

= - kx для маятника k=1

= - x

x(t)=x₀+sin(t)

x₀=0

=cos(t)

x=sin(t)

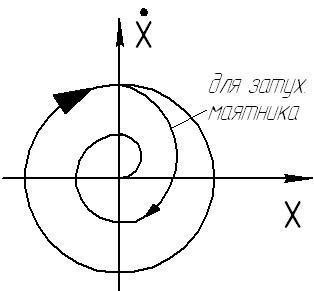Затухающий маятник.

-фазовая плоскость, фазовый портрет системы

Устойчивости соответствует стремление системы к равновесию.

Для того чтобы система автоматического регулирования могла нормально выполнять предписанные ей функции, необходимо прежде всего обеспечить устойчивость ее движения. В процессе работы на систему действуют различные возмущающие силы, вызывая отклонение ее от заданного закона движения. Если под влиянием возмущения система отклонилась от состояния равновесия или заданного закона движения и после прекращения действия внешнего возмущения снова возвращается к исходному состоянию, то движение в системе является устойчивым, сходящимся к исходному состоянию.

Если под влиянием возмущения система, будучи отклонена от состояния равновесия или от заданного закона движения, после прекращения действия возмущения не возвращается к исходному состоянию и при этом удаление системы от первоначального состояния с течением времени возрастает настолько, что отклонение выходит за пределы допустимой области, то движение в системе является неустойчивым.

Устойчивость по Ляпунову:

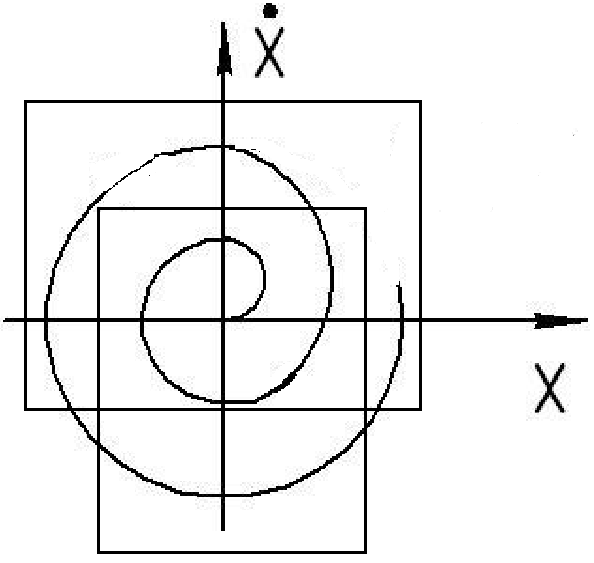
S(t) – траектория. Система f(t) называется

устойчивой по Ляпунову, если для любой

точки области E>0 существует область δ,

такая, что для любого движения, начавшегося в области Е с течением времени не покинет область δ