РГР / ТАУ практика / 4 Устойчивость

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОСИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНГИЮ

ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

ЮЖНОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА В

г. ТАГАНРОГЕ

Факультет автоматики и вычислительной техники

Кафедра систем автоматического управления__

© Тесленко О.А.

Практическое занятие 4

Дисциплина «Основы автоматического управления»

Тема: Исследование устойчивости систем автоматического управления

Таганрог 2010

Проработать материалы лекций Л8.,Л9.

1.Алгебраические критерии устойчивости Гурвица

Для устойчивости линейных систем необходимо и достаточно, чтобы при все главных определителей матрицы Гурвица были положительны.

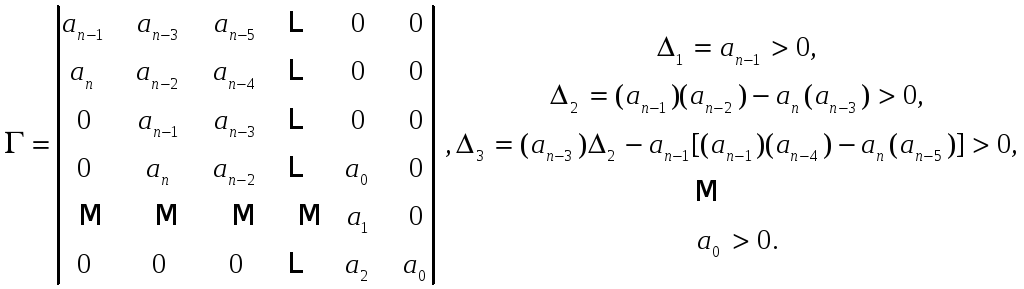
Пример 1

Пример 1

Дано. Структурная схема САУ представлена на рис.1.

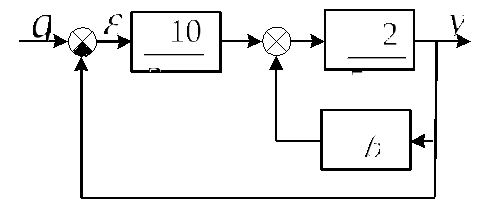
Рис.1

Требуется определить с помощью критерия устойчивости Гурвица, в каких пределах можно изменять коэффициент усиления местной положительной ОС , чтобы САУ оставалась устойчивой?

Решение

Для того чтобы воспользоваться критерием устойчивости Гурвица, необходимо определить

.

характеристический полином замкнутой системы имеет вид

. (1)

необходимое условие устойчивости – положительность всех входящих в коэффициентов . Т.е.

,

,

.

Таким образом, границы изменения коэффициента ПОС .

Графическое изображение границ устойчивости коэффициента представлено на рис.2.

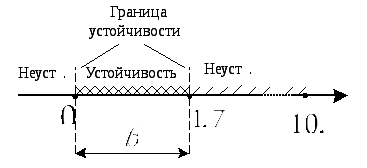
Рис.2

Пример 2

Дано. Структурная схема САУ представлена на рис.3.

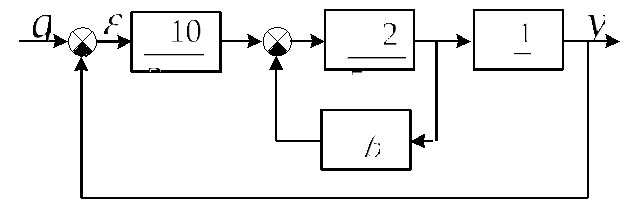
Рис.3

Требуется определить с помощью критерия устойчивости Гурвица, в каких пределах можно изменять коэффициент усиления местной положительной ОС , чтобы САУ оставалась устойчивой?

Решение

Для того чтобы воспользоваться критерием устойчивости Гурвица, необходимо определить

. (2)

характеристический полином замкнутой системы имеет вид

. (3)

Проверим необходимые условия устойчивости – положительность всех входящих в коэффициентов . Т.е.

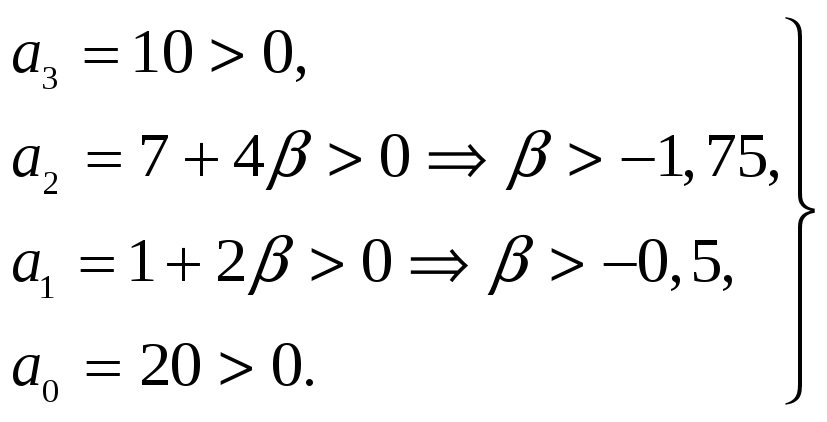выполняются при любых .

Затем необходимо определить достаточные условия, для этого составим матрицу Гурвица

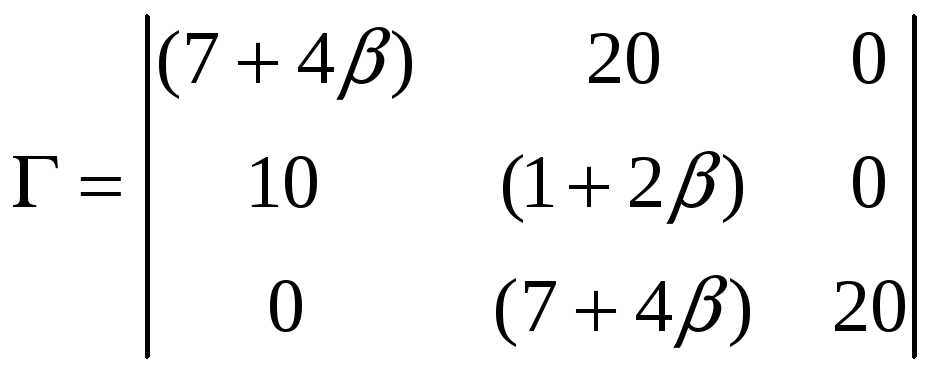
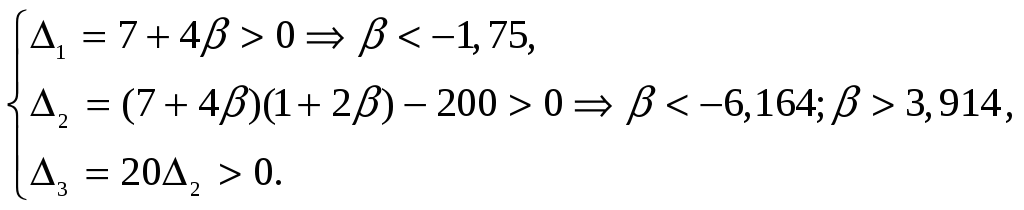
Таким образом, коэффициент оОС может быть любым положительным .

2. Критерий устойчивости Михайлова

Для устойчивости линейной системы -порядка необходимо и достаточно, чтобы изменение аргумента функции при изменении частоты равнялось бы , то есть

при .

Пример 3

Рассмотрим характеристический полином (1) с учетом

.

Чтобы построить Годограф Михайлова, необходимо определить функцию посредством замены в характеристическом полиноме и выделить действительную и мнимую части

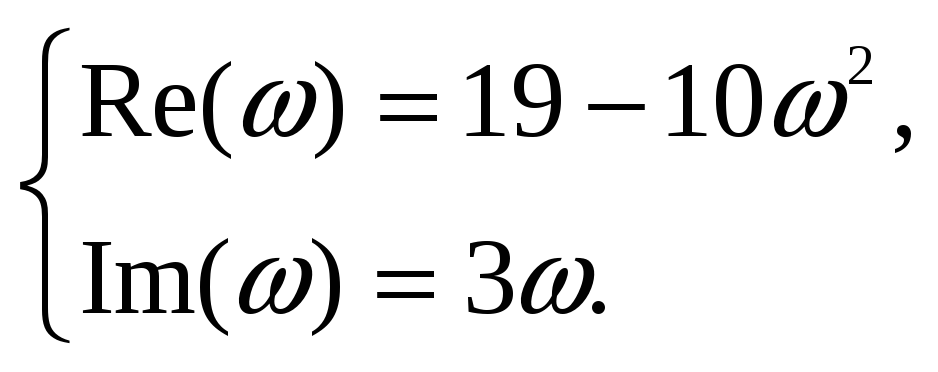
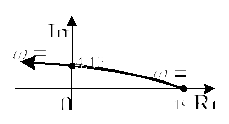
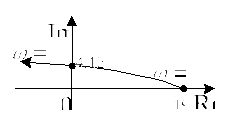
Составим таблицу значений и при изменении и построим годограф

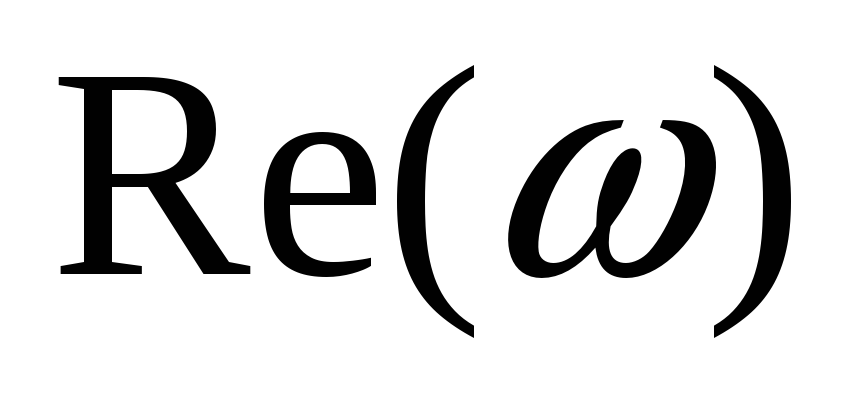
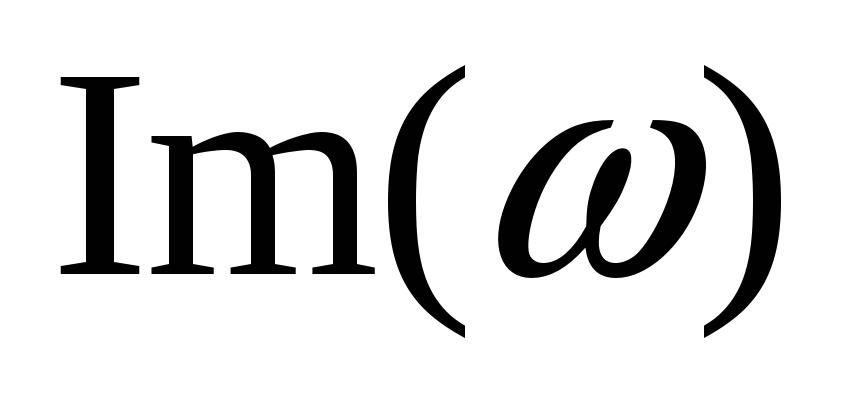
0	19	0
1,378	0	4,135

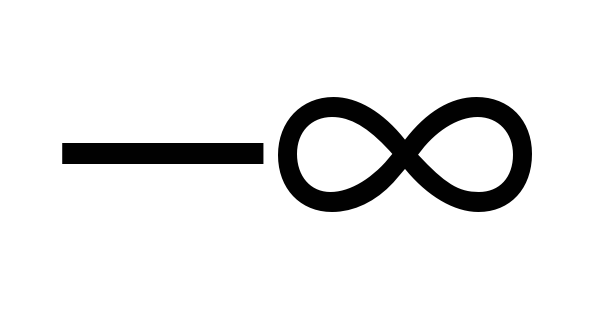
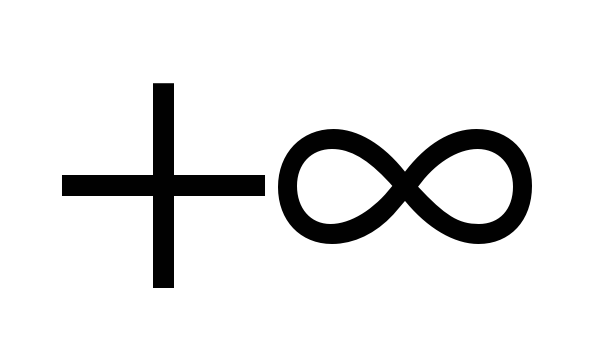
Рис.4

Согласно критерию устойчивости Михайлова, рассматриваемая САУ – устойчива.

Если выбрать в характеристическом полиноме (1) с учетом , то

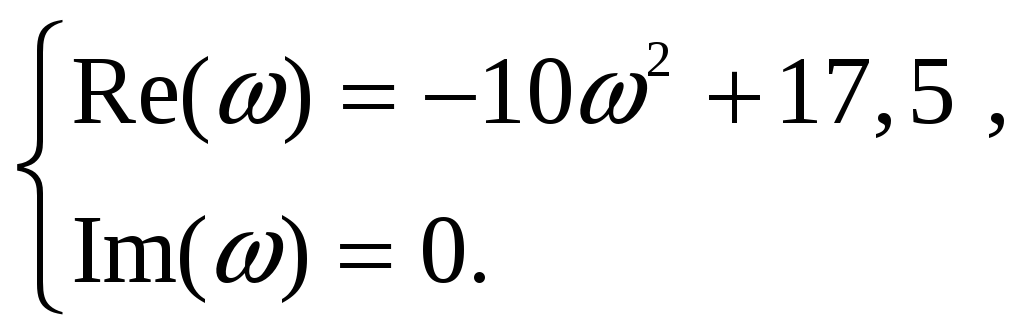
Годограф Михайлова будет иметь вид

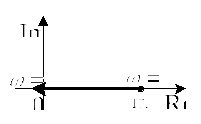
Рис.5

Согласно критерию устойчивости Михайлова, рассматриваемая САУ при является неустойчивой.

Пример 4

Рассмотрим характеристический полином (3) с учетом

.

Тогда

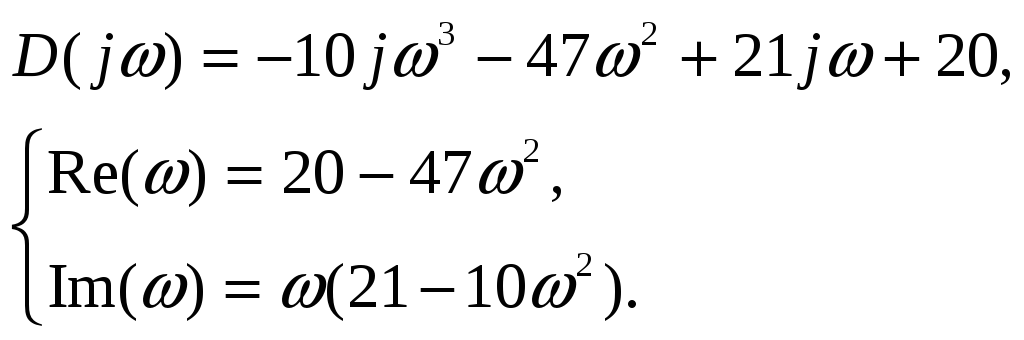
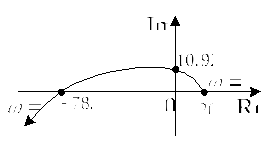
Составим таблицу значений и при изменении и построим годограф

0	20	0
0,652	0	10,923
1,45	–78,7	0

Рис.5

Согласно критерию устойчивости Михайлова, рассматриваемая САУ при устойчива.

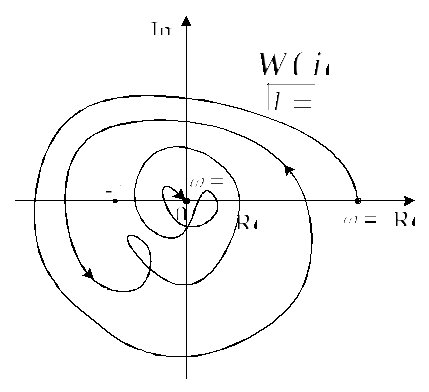
3.Критерий устойчивости Найквиста

Общая формулировка критерия Найквиста

Для устойчивости замкнутой системы автоматического регулирования необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов частотного годографа комплексного коэффициента передачи разомкнутой системы через отрицательную полуось от до была равна , где – число корней характеристического уравнения разомкнутой системы, лежащих в правой полуплоскости. Для систем, находящихся в разомкнутом состоянии на границе устойчивости с нулевыми корнями характеристического уравнения годограф берётся с дополнением в бесконечности

Пример 5

Рассмотрим передаточную функцию разомкнутой части

системы, приведенной на рис.3 с учетом

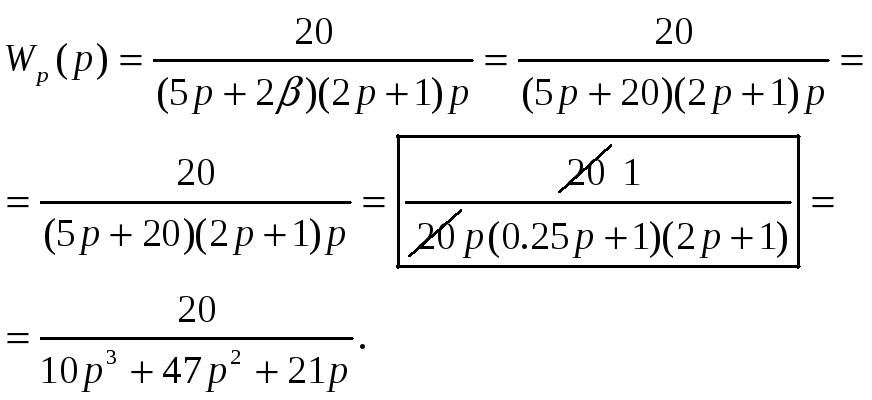(3)

Для перехода в частотную область необходимо выполнить замену и разделить действительную и мнимую части.

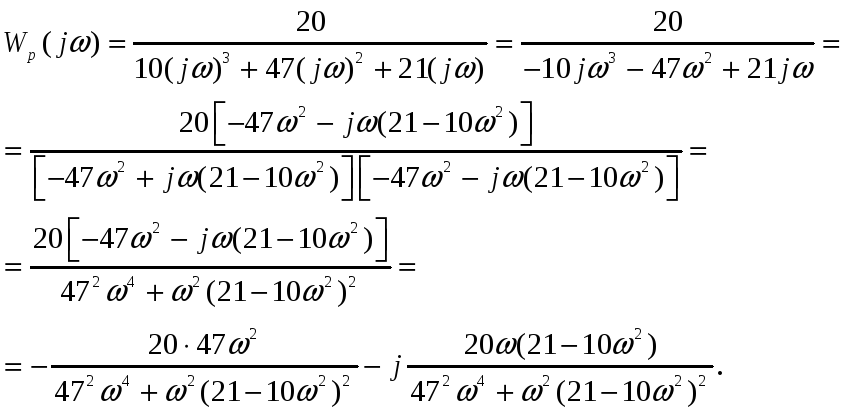Таким образом

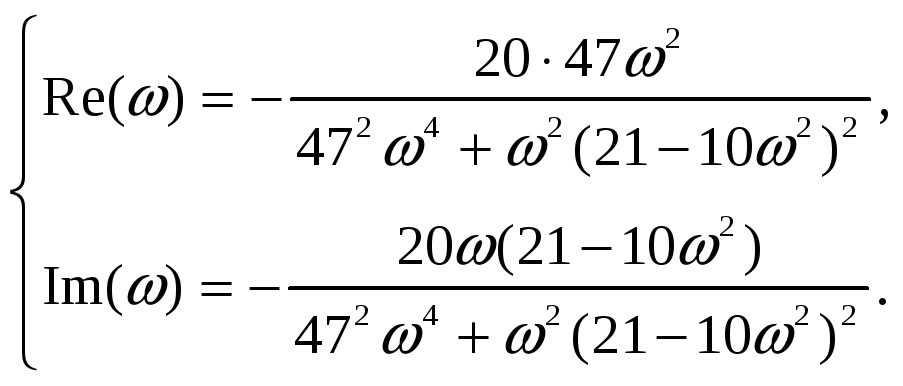
Составим таблицу значений и при изменении и построим годограф

0	–2,160
0,449	–0,202	0
0,6	–0,856	–0,528
	–0	0

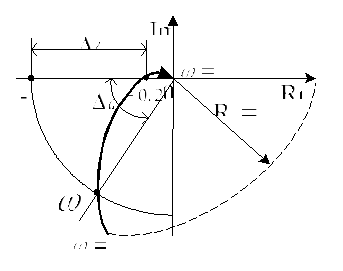
Рис.6

На рис.7 изображены ЛАЧХ и ЛФЧХ, а также определены запасы по амплитуде и фазе.

Для того, чтобы построить ЛАЧХ и ЛФЧХ необходимо преобразовать (3) к виду

,

И определить сопрягающие частоты: и , далее изучить Л.5, и на основании полученных знаний, построить характеристики.

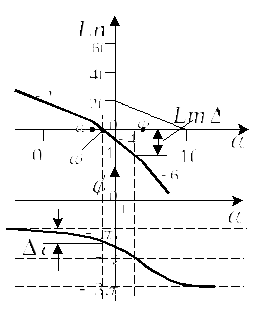
Рис.7

Домашнее задание

1. Исследовать устойчивость САУ, и определить 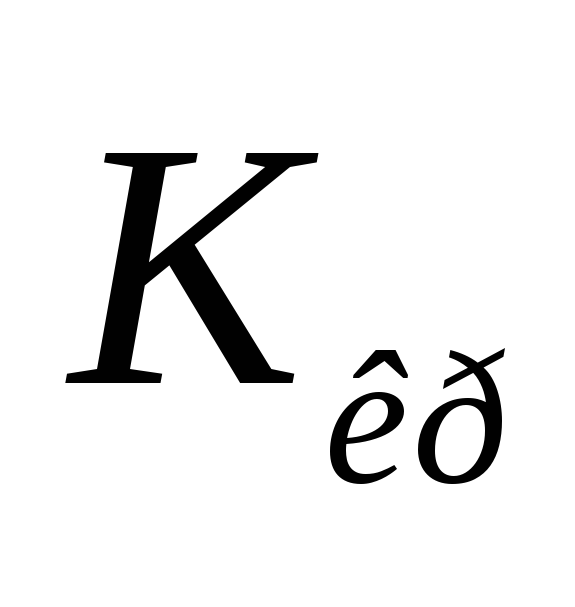по характеристическому полиному

с помощью критерия Гурвица.

2. Исследовать устойчивость САУ по критерию Гурвица и построить области устойчивости по параметру 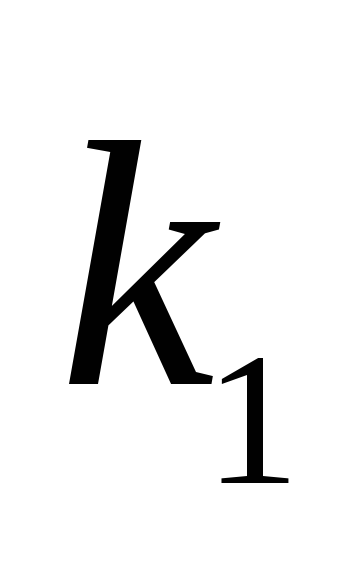, если 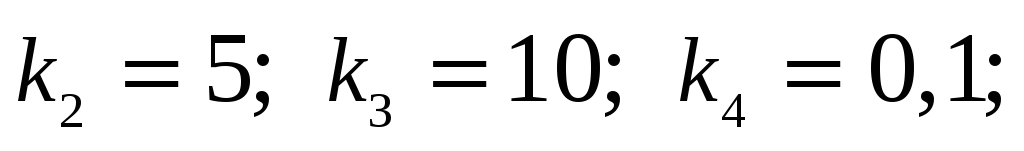, 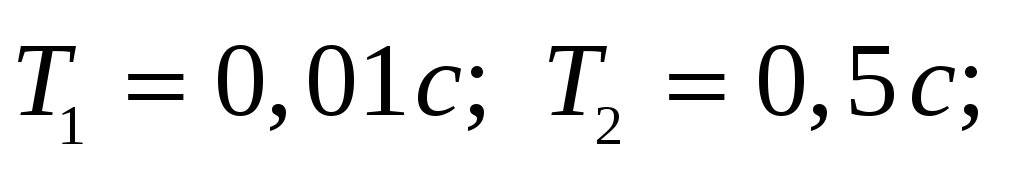. Структурная схема САУ представлена на рис.8. Определить вид корректирующего устройства.

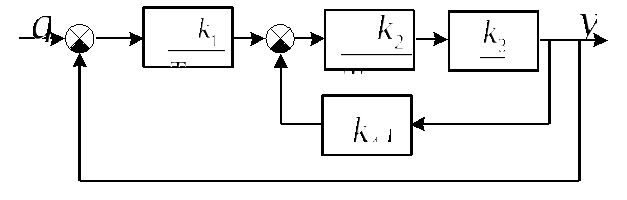
Рис.8

2. Построить годограф Михайлова для устойчивой и неустойчивой САУ представленной на рис.8.

3. Построить годограф Найквиста для устойчивой и неустойчивой САУ, представленной на рис.8, определить запасы по амплитуде и фазе.

4. По амплитудно-частотным характеристикам разомкнутых систем, проведенных на рис.9,10,11 проанализировать устойчивость замкнутых систем регулирования.

Рис.9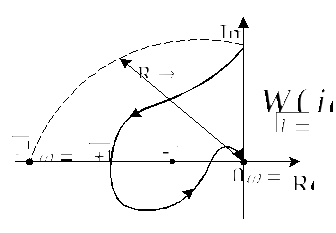

Рис.10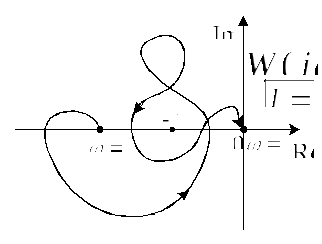

Рис.11

9