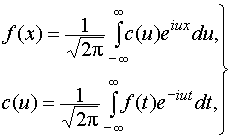Интеграл Фурье в комплексной форме
Преобразуем подынтегральное выражение формулы (24) по формулам Эйлера:
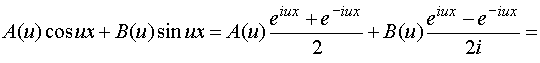
где
(30)
Подставляем в формулу (24):
во втором слагаемом сделаем подстановку: w = - u, du = - dw, а затем используем свойства неопределённого и определённого интегралов:
· первообразная не зависит от обозначения аргумента;
· если в определённом интеграле пределы поменять местами, интеграл изменит знак;
· если интервал интегрирования разбить на части (например, точкой и = 0), то интеграл по всему интервалу равен сумме интегралов по каждой из его частей.
Итого:
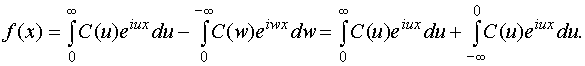
Окончательно
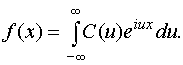(31)
Вернёмся к равенствам (30), подставляя в них значения коэффициентов А(и), В(и) по формулам (25):
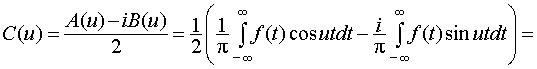
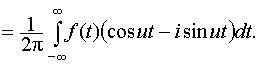
Окончательно
(32)
Функцию С(и) в формуле (32) называют обратным преобразованием Фурье.
Выражение для f(x) в виде (31) называется комплексной формой интеграла Фурье (или прямым преобразованием Фурье).
Объединим формулы (31) и (32):
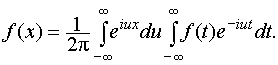
Внесём еiux под знак внутреннего интеграла (относительно переменной t интегрирования этот множитель является константой):
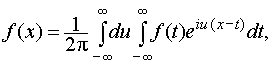(33)
правая часть формулы называется двойным интегралом Фурье в комплексной форме.
По аналогии с пунктом 10 (см. формулы (26/ ), (28/ )) получим симметричную форму записи выражений (31) и (32). Положим
Тогда
|
|
(34) |
где комплексную функцию с(и) по-прежнему называют преобразованием Фурье функции f(x) (или обратным преобразованием Фурье).
Замечание 1. Формулы
(26), (28) и (26/
), (28/
), так же как формулы (31 – 33) и (34), отличаются
только коэффициентом: либо это
,
либо
,
либо
.
В связи с этим надо быть внимательными
при пользовании таблицами преобразований
Фурье.
Пример 7. Представить интегралом Фурье функцию
Рис.
19
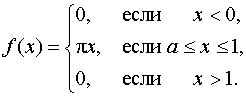
Решение. Функция удовлетворяет условиям теоремы Фурье: имеет одну точку разрыва (см. рис. 19) и абсолютно интегрируема:
Воспользуемся комплексной формой интеграла Фурье (33)
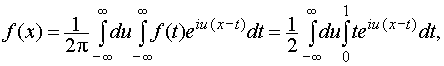
интегрируем по частям:
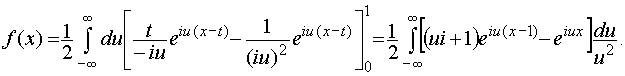
Замечание 2. В электротехнике формулы (31) и (32) используются в другой символике. Заменив аргумент и на z, получим по формуле (32) функцию
(35)
которую
называют спектральной плотностью
функции f(x)
(или обратным преобразование Фурье),
называют
амплитудным спектром функции f(x).
Соответственно перепишем формулу (31) прямого преобразования Фурье:
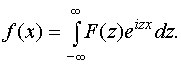(36)
Замечание 3. Если функция f(x) известна, то формулу (36) можно рассматривать как интегральное уравнение относительно неизвестной функции F(z). Тогда решение этого уравнения находят по формуле (35).
Пример 8. Найти преобразование Фурье для функции
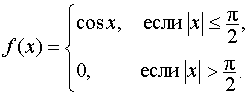
Решение. Функция
удовлетворяет условиям Дирихле и
абсолютно интегрируема на
:
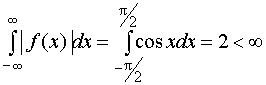
Изобразим график функции (см. рис. 20). Функция чётная, поэтому достаточно найти косинус-преобразование Фурье по формуле (26):
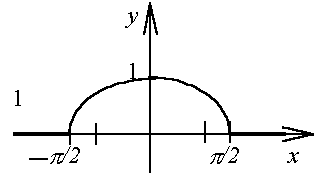Рис.
20
=
=
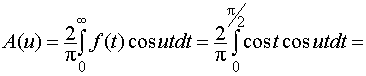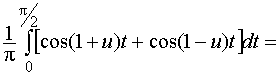
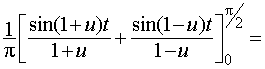
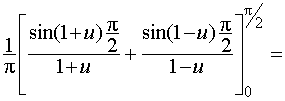
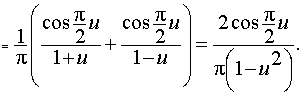
Использовали тригонометрическую формулу
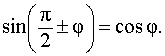
Пример 9. Решить уравнение
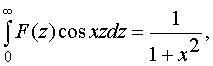
Решение.
В
данном интегральном уравнении неизвестной
является функция F(z).
Правая часть уравнения – чётная функция
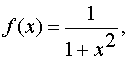поэтому
левую часть уравнения можно рассматривать
как интеграл Фурье для чётной функции
(см. формулы 26)
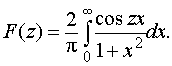
Этот интеграл мы нашли в примере 6 и, значит, F(z) = e- z.