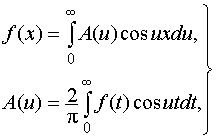Комплексная форма ряда Фурье для функции с периодом

Пусть функция у = f (x) удовлетворяет условиям Дирихле и ряд Фурье этой функции имеет вид

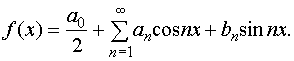(10)

Преобразуем слагаемые суммы с помощью формул Эйлера:

где

Полагая перепишем формулу (10):

Найдём формулы коэффициентов с_n:

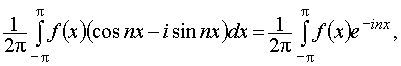= п > 0.

Непосредственно видно, что эта формула верна и для п = 0, и для п <  0 (последнее видно, например, из того, что ; обозначает комплексное число, сопряжённое с. Итак,

, (11)

где .

Правая часть формулы (11) представляет собой комплексную форму ряда Фурье с периодом .

Интеграл Фурье (как предельный случай ряда Фурье)

Всякую функцию f(x), удовлетворяющую условиям Дирихле, можно разложить на интервале (- е, е) в тригонометрический ряд по формуле (19):

(19)

где n = 0, 1, 2, ... ,

Полученное разложение будет справедливо на всей оси ох, если функция f(x) = f(х + 2е), т. е. 2е-периодична.

Рассмотрим предельный случай, когда , т. е. непериодической функции, заданной для всех .

Предположим, что:

·  на всяком конечном отрезке оси ох функция f(x) удовлетворяет условиям Дирихле;

·  сходится несобственный интеграл

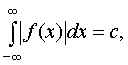c = const

(функция в этом случае называется абсолютно интегрируемой).

Сначала преобразуем формулу (19^/ ), подставив в неё формулы коэффициентов:

затем используем свойство определённого интеграла (от суммы функций) и тригонометрическую формулу

,

тогда

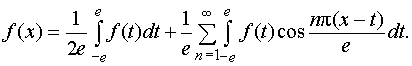     (22)

Оценим первое слагаемое выражения (22) при условии, что , используя сходимость несобственного интеграла:

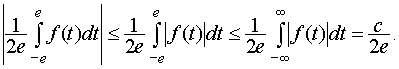
Заметим, что

Для оценки второго слагаемого из (22), при , введём новую переменную и, которая принимает значения членов арифметической прогрессии:

с разностью

Тогда

где

Переходя к пределу при , учитывая, что напоминает интегральную сумму, получим

(23)

Правая часть формулы (23) называется двойным интегралом Фурье.

Нетрудно убедиться, что в формуле (23) внутренний интеграл является чётной функцией переменной и, поэтому, используя свойства определённого интеграла, можно записать ещё один вид интеграла Фурье:

Перейдём к другой форме записи интеграла Фурье в виде однократного интеграла. Воспользуемся той же тригонометрической формулой и преобразуем формулу (23):

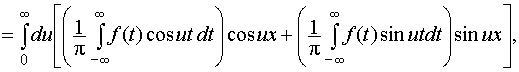
(24)

где

(25)

Выражение (24) называется формулой Фурье, а интеграл в правой части называется интегралом Фурье.

Теорема 1 Фурье. Если:

· функция f(x) удовлетворяет условиям Дирихле на всяком конечном отрезке, т. е. кусочно монотонна и имеет конечное число точек разрыва,

· f(x) абсолютно интегрируема на интервале ,

то имеет место равенство (24), причём

где А(и), В(и) вычисляют по формулам (25).

На практике чаще пользуются другим достаточным признаком, поскольку требование абсолютной интегрируемости функции по бесконечному промежутку оказывается стеснительным.

Теорема 2. Если:

· функция f(x) абсолютно интегрируема в каждом конечном промежутке[x₁, x₂] т. е.

· для (N — достаточно большое число) функция f(x) монотонна, причём

то в каждой точке х интеграл Фурье сходится и имеет место равенство (24).

Рассмотрим частные случаи формулы (24):

1. Пусть f(x) — чётная функция, тогда В(и) = 0,

(26)

или, объединяя обе формулы,

(27)

Правая часть выражения (27) называется двойным интегралом Фурье для чётной функции.

Функция А(и) в формуле (26) называется косинус-преобра-зованием Фурье.

2. Пусть f(x) — нечётная функция, тогда А(и) = 0,

(28)

или

(29)

Правую часть выражения (29) называют двойным интегралом Фурье для нечётной функции, а функцию В(и) в выражении (28) называют синус-преобразованием Фурье.

Замечание. В учебной литературе Вы можете встретить другую запись интеграла Фурье, называемую симметричной. Получим эти формулы. Положим

Тогда:

1) для чётной функции, т. е. f(x) = f(- x), имеем

(26/ )

где а(и) — косинус-преобразование Фурье для чётной функции;

2) для нечётной функции, т. е. f(- x) = - f(x), имеем

(28/ )

где b(и) — синус преобразование Фурье для нечётной функции.

По аналогии с рассуждениями п. 7 рассмотрим вариант, когда функция f(x) определена лишь на полуоси, например, , то, продолжая её чётным или нечётным образом на интервал , мы получаем возможность представить эту функцию интегралом Фурье, либо по формулам (26 – 27), либо по формулам (28 – 29) с пределами интегрирования от 0 до , что и соответствует области определения функции. Естественно, что представление f(x) интегралом Фурье будет справедливо лишь на полуоси .

Итак:

1) интеграл Фурье можно рассматривать как предельный случай (при ) ряда Фурье;

2) интеграл Фурье представляет собой двухкратный интеграл от функции двух аргументов (и, t), кроме того, зависящий от параметра х. Выполняя внутреннее интегрирование по аргументу t в формуле (23), мы получаем функцию двух переменных и, х. Выполняя затем внешнее интегрирование по и и деля результат на , получаем f(x).

Если х — точка разрыва (функция терпит скачок), то под символом f(x) в формуле (23) следует понимать полусумму её односторонних пределов в этой точке:

(см. теорему Дирихле).

Пример 6. Представить интегралом Фурье функцию f(x) = e^-x, , продолжив её на промежуток : а) чётным образом, б) нечётным образом.

Используя полученные формулы, вычислить интегралы

Решение. Функция удовлетворяет условиям Дирихле и абсолютно интегрируема на интервале :

а) Продолжим функцию на интервал чётным образом (см. рис. 17). Новая функция также отвечает условиям Дирихле и абсолютно интегрируема на каждом конечном отрезке [x₁, x₂] оси ох, т. е. выполняются условия теоремы 2:

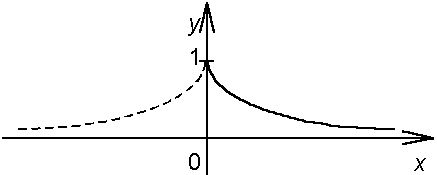Рис.17

Воспользуемся формулами (26),

где

Последний интеграл является циклическим, интегрируя дважды по частям, получим ответ. Можно воспользоваться готовой формулой

Подставив а = - 1, b = u, получаем

Подставляем найденный коэффициент А(и) в первую из формул (26)

где f(x) = e^{- x} по условию.

Записываем интеграл Фурье

, или

б) Продолжим функцию e^-x нечётным образом (см. рис. 18). Функция нечётная, поэтому воспользуемся формулами (28). Найдём синус-преобразование Фурье:

Рис. 18

Воспользуемся формулой

при а = - 1, b = u имеем

Искомый интеграл Фурье запишем по формуле

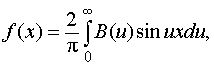
где f(x) = e^-x по условию;

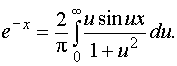
Теперь ответим на последний вопрос, выделив нужные интегралы из полученных формул, предварительно положив х = 1 в каждой из них. Тогда соответственно из пункта (а) имеем

откуда следует

из пункта (б) имеем

откуда следует

Мы получили числовые значения двух несобственных интегралов, тем самым доказав их сходимость.