РГР / raschetnaya_rabota_issledovanie_sau

Содержание:

1. Переход от передаточной функции к модели объекта в переменных состояния	3
2. Дифференциальное уравнение	3
3. Аналитическое выражение для всех частотных характеристик	4
4. Амплитудно-фазовая характеристика объекта	5
5. АЧХ и ЛАЧХ	6
6. ВЧХ и МЧХ	7
7. Структурная схема системы, соответствующая дифференциальному уравнению	8
8. Проверка устойчивости системы	10
8.1. По критерию Гурвица	10
8.2. По критерию Михайлова	11
8.3. По критерию Найквиста	11
9. Полная статическая ошибка	12
10. Оценка качества переходного процесса системы по ВЧХ	12
11. Проверка управляемости объекта по полученной системе дифференциальных уравнений	13
12. Проверка наблюдаемости объекта по полученной системе дифференциальных уравнений	13
13. Синтез системы, в которой качество процессов будет отвечать требованиям , ,	14

1. Переход от передаточной функции к модели объекта в переменных состояния

Передаточная функция объекта:

.

Дифференциальное уравнение данной системы управления (вывод в пункте 2):

.

Перейдем к модели объекта следующего вида:

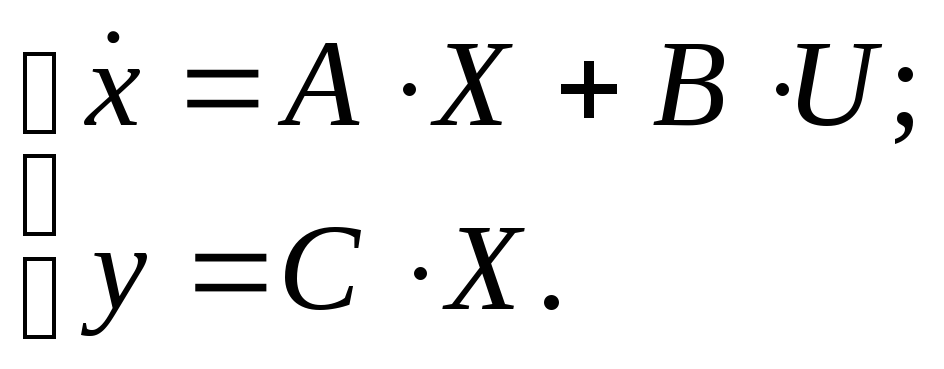
Введем переменные состояния:

Следовательно:

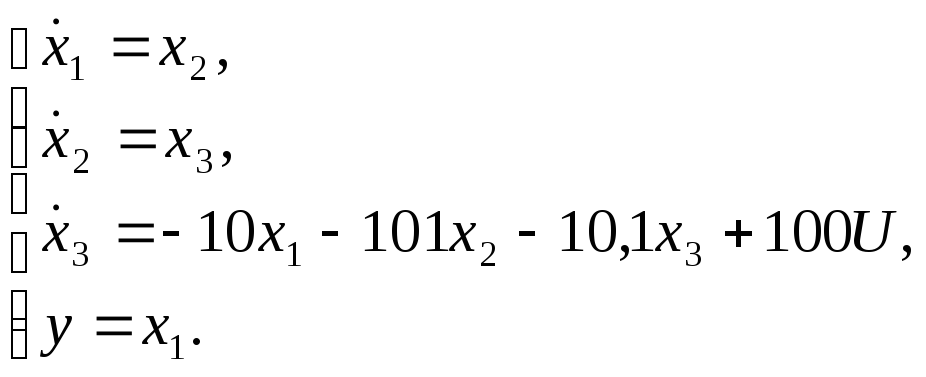
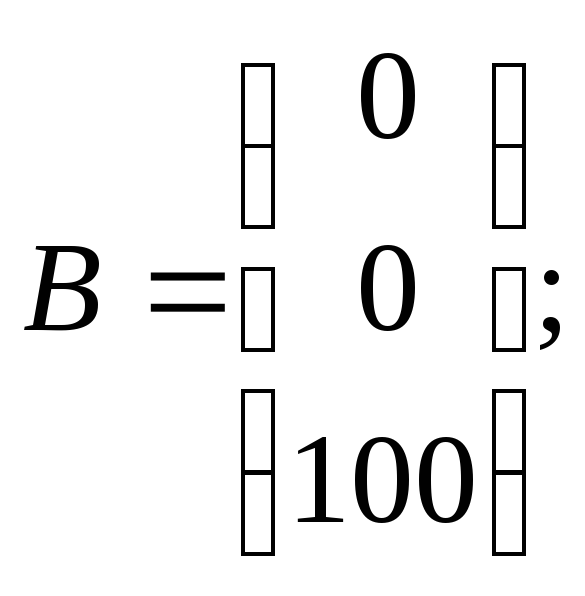
2. Дифференциальное уравнение

Передаточная функция объекта управления: , откуда , или , , следовательно, производя обратное преобразование Лапласа, получим дифференциальное уравнение данной системы управления:.

Левая часть этого дифференциального уравнения характеризует выходные параметры системы.

Правая часть характеризует входные воздействия.

3. Аналитическое выражение для всех частотных характеристик

Для получения аналитического выражения амплитудно-фазовой частотной характеристики сделаем подстановку в передаточной функции:

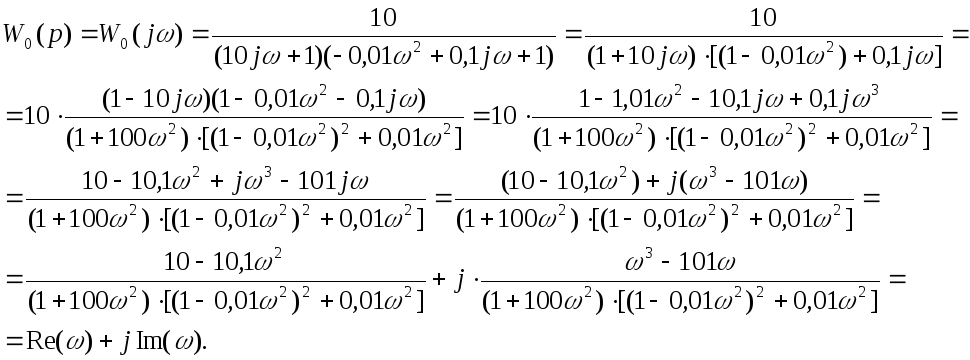
Следовательно, вещественная частотная характеристика может быть выражена аналитически следующим образом:

Выражение для мнимой частотной характеристики имеет вид:

Определим аналитическое выражение для амплитудной частотной характеристики:

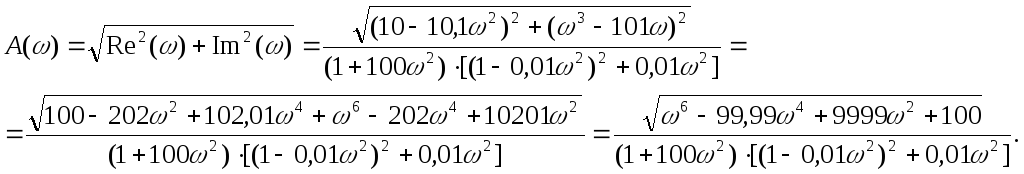
Аналитическое выражение для фазовой частотной характеристики:

Логарифмическая амплитудная характеристика:

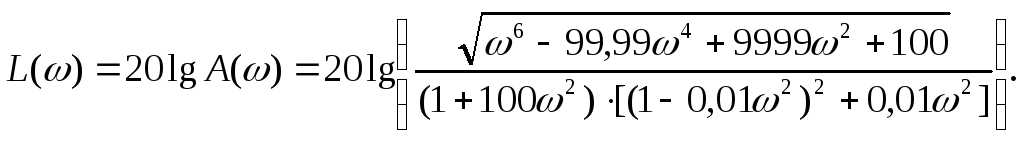
4. Амплитудно-фазовая характеристика объекта

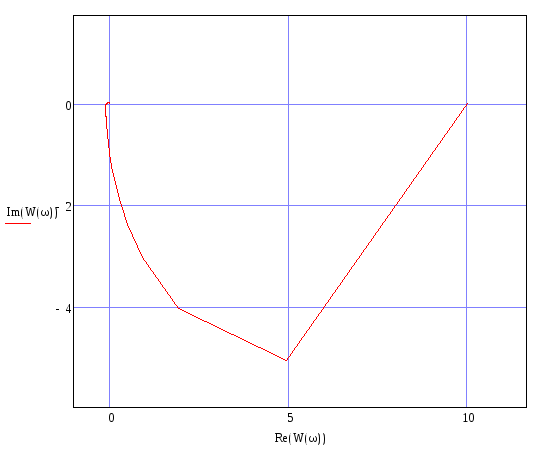
Рисунок 1. Амплитудно-фазовая частотная характеристика (годограф).

5. АЧХ и ЛАЧХ

Рисунок 2. Амплитудная частотная характеристика.

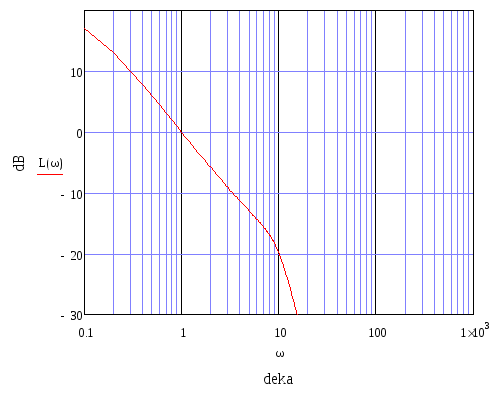
Рисунок 3. Логарифмическая амплитудная частотная характеристика.

6. ВЧХ и МЧХ

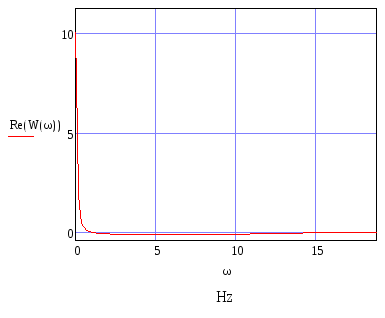
Рисунок 4. Вещественная частотная характеристика.

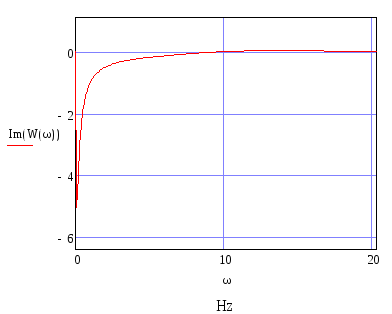
Рисунок 5. Мнимая частотная характеристика.

7. Структурная схема системы, соответствующая дифференциальному уравнению

Дифференциальное уравнение системы:

Передаточная функция объекта:

.

Структурная схема объекта:

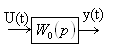
Представим передаточную функцию объекта через произведение передаточных функций нескольких более простых, последовательно соединенных звеньев, тогда структурная схема примет вид:

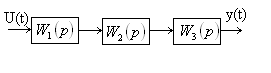
В этом случае сигналы через звенья:

; ; .

Представим передаточную функцию объекта через сумму передаточных функций нескольких более простых, параллельно соединенных звеньев, для чего воспользуемся методом неопределенных коэффициентов:

- пусть , где

А, B, C – неизвестные коэффициенты, которые нужно вычислить.

Перейдем к уравнению .

Приведем правую часть уравнения к общему знаменателю:

, тогда

;

.

Таким образом, можно перейти к системе:

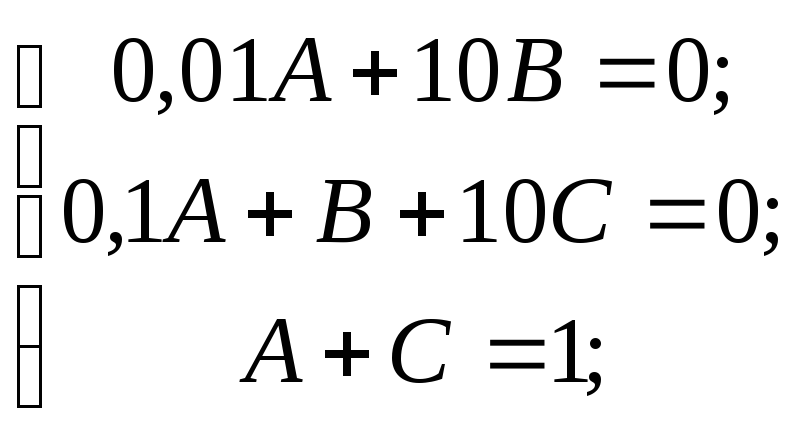
Подставим вычисленные коэффициенты в выражение для суммы:

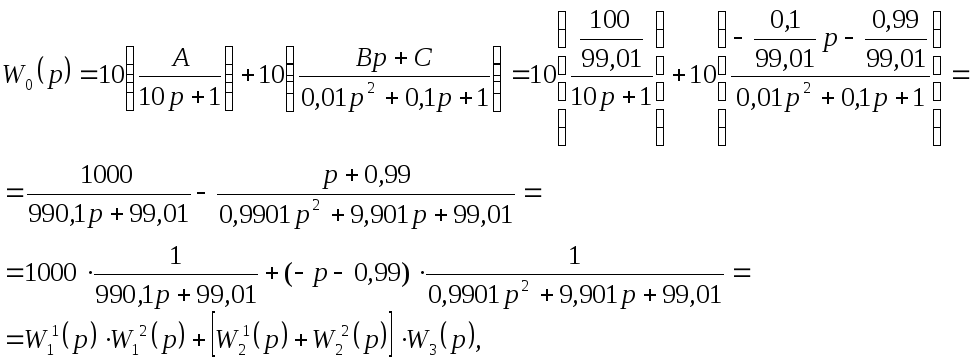
где:

Структурная схема объекта примет вид:

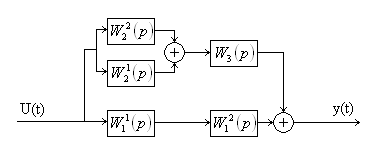
Сигналы через звенья:

8. Проверка устойчивости системы

8.1. По критерию Гурвица

Дифференциальное уравнение системы:

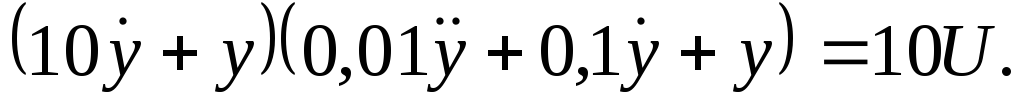
Характеристическое уравнение системы:

;

.

Многочлен

=0,1; =1,01; =10,1; =1.

Определитель Гурвица:

Диагональные миноры определителя Гурвица:

1.

2.

Главный определитель:

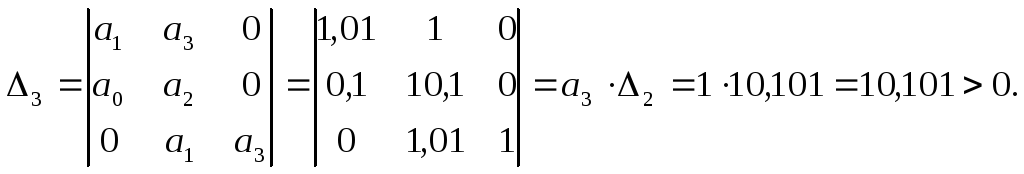
Так как определитель Гурвица и все его диагональные миноры положительны, то система устойчива по критерию Гурвица.

8.2. По критерию Михайлова

Многочлен

Сделаем подстановку :

Построим годограф Михайлова:

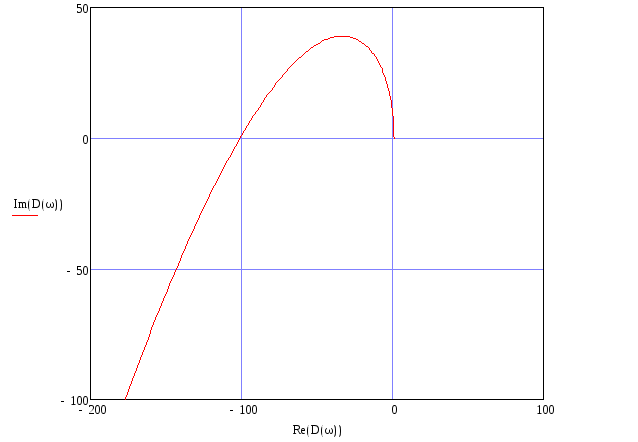
Рисунок 6. Годограф Михайлова.

Видно, что годограф Михайлова, начинаясь на действительной положительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно 3 квадранта (система 3-го порядка), что означает, что исследуемая система устойчива по критерию Михайлова.

8.3. По критерию Найквиста

Передаточная функция системы имеет вид:

.

АФХ разомкнутой системы приведена в пункте 4. Видно, что годограф АФХ разомкнутой системы не охватывает точку (-1;j0), следовательно, замкнутая система устойчива.

9. Полная статическая ошибка

Статическая ошибка – это расхождение установившегося значения сигнала после переходного процесса с требуемой величиной выходного сигнала:

.

Установим произвольно некоторое заданное значение регулируемой величины:

.

Начальное значение ВЧХ равно установившемуся значению переходной характеристики:

Тогда полная статическая ошибка:

При данном заданном значении регулируемой величины данная система имеет статическую ошибку 5%.

10. Оценка качества переходного процесса системы по ВЧХ

Данная система автоматического управления имеет вогнутую вещественную частотную характеристику, что позволяет судить о монотонной переходной характеристике и отсутствии перерегулировки.

Время переходного процесса можно оценить приблизительно по виду ВЧХ. Оно определяется полосой частот, при которых . Эта полоса называется интервалом положительности . При этом всегда >/. В нашем случае . Значит >10c.

11. Проверка управляемости объекта по полученной системе дифференциальных уравнений

Для проверки управляемости объекта запишем матрицу управляемости:

Вычислим произведения матриц:

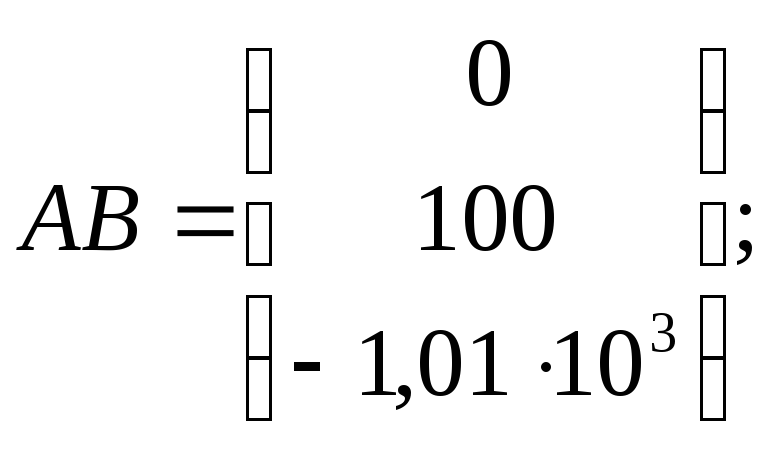
Матрица управляемости:

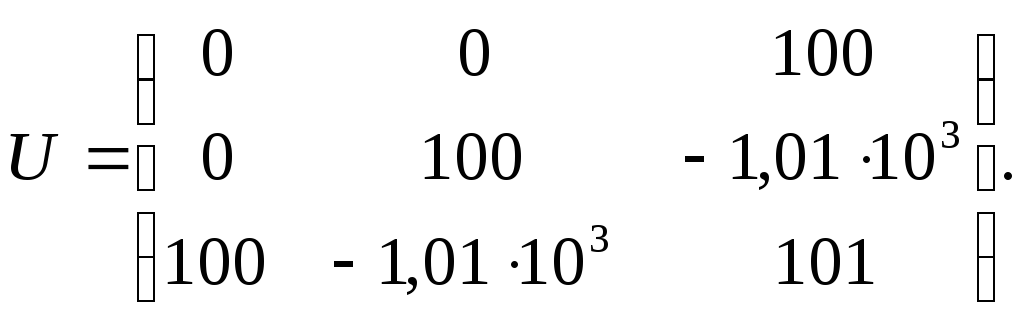
Определитель матрицы управляемости:

Т.к. матрица U не вырождена , то система управляема по критерию управляемости.

12. Проверка наблюдаемости объекта по полученной системе дифференциальных уравнений

Для проверки наблюдаемости объекта запишем матрицу наблюдаемости:

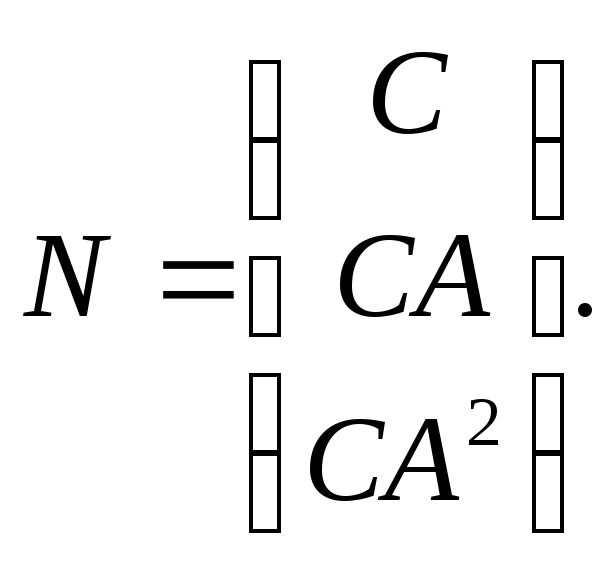
Вычислим произведения матриц:

Матрица наблюдаемости:

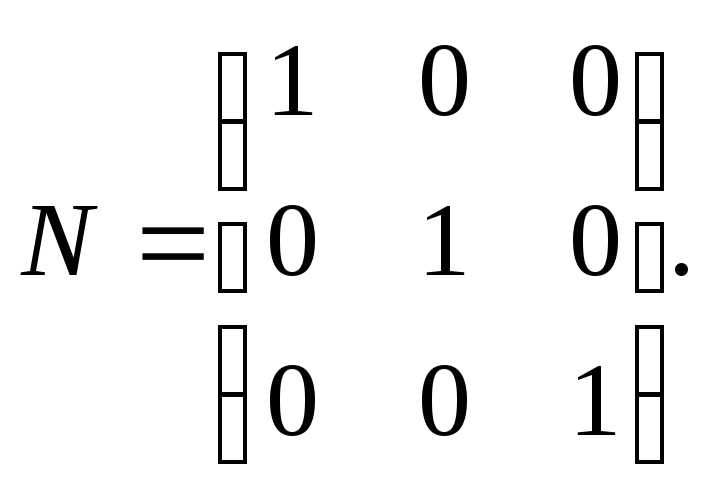
Определитель матрицы наблюдаемости:

Т.к. матрица N не вырождена , то система наблюдаема по критерию наблюдаемости.

13. Синтез системы, в которой качество процессов будет отвечать требованиям , ,

Передаточная функция исходной системы автоматического управления имеет вид:

.

Для определения параметров регулятора используем операторную процедуру модального метода синтеза.

В качестве корректора статики используем интегрирующее звено с передаточной функцией

,

что гарантирует нулевую статическую ошибку в системе .

С целью обеспечения требуемых динамических свойств формируем корректор динамики в виде

, , , - неизвестные коэффициенты регулятора.

Запишем характеристическое уравнение замкнутой системы:

Желаемое характеристическое уравнение тоже должно быть 4-го порядка. Выберем распределение корней так, чтобы они обеспечивали заданное качество процессов.

Т.к. в системе не допускается перерегулирование, корни должны быть вещественными, располагаться в левой комплексной полуплоскости не ближе к мнимой оси.

Исходя из этих ограничений, зададимся произвольными корнями желаемого характеристического полинома:

Тогда желаемый характеристический полином будет иметь вид:

Приравняем характеристический полином замкнутой системы к желаемому характеристическому полиному:

Таким образом, можно перейти к следующей системе:

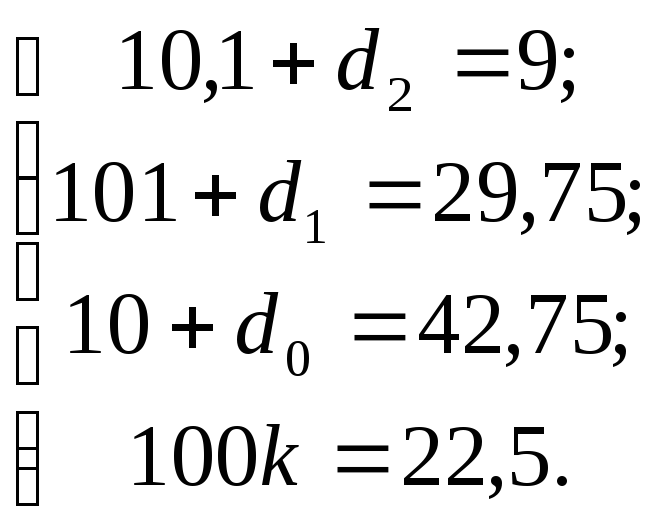
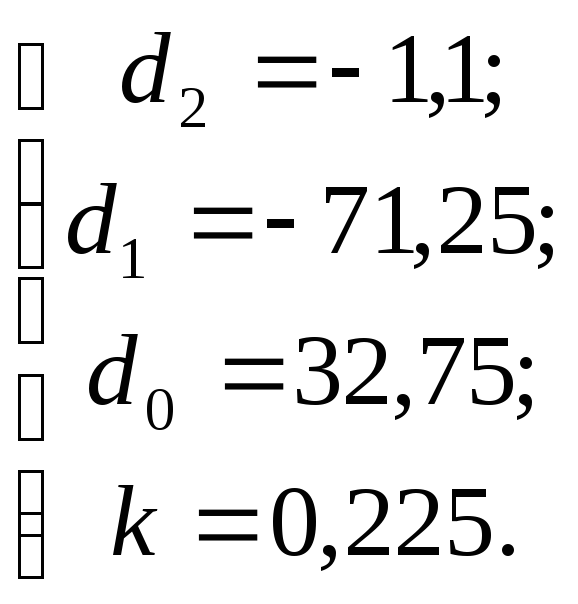
Подставим полученные значения коэффициентов в передаточные функции корректоров статики и динамики:

Передаточная функция синтезированной системы имеет вид:

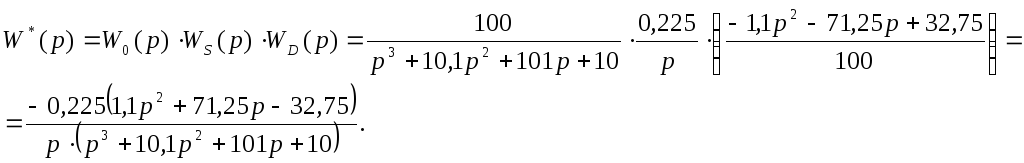
Список использованных дополнительных источников информации:

1. Бесекерский В.А., Попов ЕЛ. Теория автоматического регулирова­ния. - М.: Наука, 1974.

2. Душин С.Е., Зотов Н.С. Теория автоматического управления. - М.: Высшая школа, 2003.

3. Курс лекций. Составил: к.т.н., доцент Тихонов А.И. 2002г.:

http://www.toehelp.ru/theory/tau/contents.html

4. Сайт «ТАУ - научно-техническая дисциплина»: http://www.tau-ntd.ru/index.html

14