1. Задание

Исходные данные:

Структурная схема исходной системы

Рис. 1. Структурная схема исходной системы

Таблица 1. Исходные значения параметров системы

k1	k2	k3	Т1, с	Т2, с	Т3, с
2,5	1,4	0,7	1,3	2	1

Распределение корней соответствует биномиальной стандартной линейной форме (A₁=2).

Измеряемая координата – х₁.

1. Синтезировать алгоритм модального управления заданным объектом при настройке биномиальной стандартной линейной форме (A₁=2), средний геометрический корень принять равным 1/ Т₁,

2. Синтезировать наблюдатель полного порядка с тем же распределением корней характеристического уравнения и среднегеометрическим корнем _н = (5…10)^., 1/с.

3. Синтезировать наблюдатель пониженного порядка с быстродействием, заданным в предыдущем пункте.

4. Синтезировать на основании модифицированного модального метода астатическую САУ с быстродействием заданным в п.1.

2. Модель объекта в пространстве состояний.

Векторно-матричная форма записи объекта управления

где - вектор-столбец координат состояний,

А, B,M - матрицы коэффициентов; dim A = nn, dim B = n1, dim M = n1.

Найдем А,B и M, для чего представим наш объект управления в виде системы линейных стационарных дифференциальных уравнений в нормальной форме Коши.

Из системы уравнений находим:

Собственная матрица ОУ

Матрица при управляющем воздействии:

Матрица при возмущающем воздействии:

Расчет установившихся значений переходных процессов

Из векторно-матричного уравнения ОУ при t ;

При управляющем воздействии: u = 1; f= 0

;

При управляющем воздействии: u = 0 f= 1

;

Переходные процессы в объекте управления

Рис. 2. Переходные процессы в объекте управления

Параметры переходных процессов.

При управляющем воздействии.

Схема при управляющем воздействии, где все сигналы на возмущение делаем равным нулю.

Установившиеся значения управляемых координат x₁ и x₂ при t → ∞:

x_уст1=0; x_уст2=2.5

Показатели качества:

1) время регулирования

T_рег1=13,1(с); T_рег2=11,2(с)

2) максимальное перерегулирование (%)

σ₁=inf; σ₂= 29,9;

При возмущающем воздействии.

Установившиеся значения управляемых координат x₁ и x₂ при t → ∞:

x_уст1= 0.468; x_уст2= -0.714

Показатели качества:

1) время регулирования

T_рег1= 1(с); T_рег2= 3.82(с)

2) максимальное перерегулирование (%)

σ₁= 29.9; σ₂= 66.8;

Результаты поиска установившихся значений координат состояния опытным путем совпали с результатами аналитических расчетов

Задача №2.

Синтезировать алгоритм модального управления заданным объектом при полных измерениях и настройке системы на желаемое распределение корней характеристического полинома, соответствующее:

- биномиальной стандартной линейной форме (A₁=2).

Среднегеометрический корень характеристического полинома САУ принять равным

Путём структурных преобразований определить установившиеся значения координат состояния системы модального управления при подаче управляющего и возмущающего воздействий.

Перед началом синтеза модального регулятора необходимо произвести проверку условия управляемости, выражаемое равенством rang(Y) = n [1]. Для заданного объекта матрица управляемости Y имеет вид

,

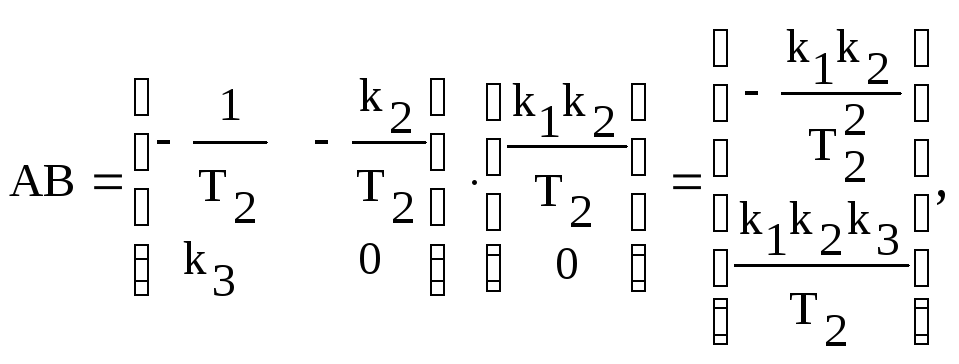
а ее диагональный минор второго порядка равен

Из последнего выражения видно, что ранг Y равен порядку ОУ rang(Y) = 2 = n, то есть объект является полностью управляемым.

В задачу синтеза закона модального управления входит нахождение коэффициентов передачи каналов отрицательных обратных связей (ООС) по координатам состояния , преднамеренное введение которых в систему обеспечивает желаемое распределение корней. Скалярное управляющее воздействиеu формируется на основании следующего закона управления [1]

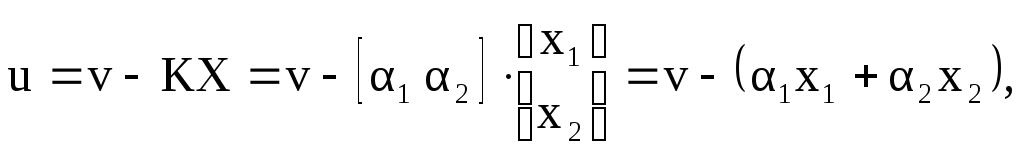
где v – скалярное задающее воздействие.

в результате чего собственные динамические свойства объекта теперь описываются определителем , который является характеристическим полиномом замкнутой системы:

Приравнивая полученный характеристический полином к стандартному виду

и выбирая среднегеометрический корень равным, а также коэффициент формы А₁ =2 (для 2-го порядка полинома), то можно определить элементы матрицы К.

Определим

Структурная схема синтезированной САУ с модальным регулятором:

Рис. 3. Структурная схема САУ с модальным управлением и полными измерениями.

Желаемая САУ моделируется в относительных единицах для универсального определения значения постоянной времени.

При биномиальной стандартной линейной форме A₁=2.

Структурная схема желаемой САУ:

Рис. 4. Структурная схема желаемой САУ

Рис. 4.1. Переходные процессы желаемой САУ

Рис. 5. Переходные процессы в СМУ под влиянием управляющего и возмущающего воздействий