14

Федеральное агентство по образованию

технический университет

Кафедра автоматизированных информационных систем

Контрольная работа № 2

по дисциплине: «Основы теории управления»

Вариант 1

Выполнил: .

студент 4 курса, специальности АИС

Шифр

Проверил: .

Ухта 2009 г.

Содержание.

1.	Задание на выполнение контрольной работы……………...	2
2.	Решение, расчет передаточной функции…………………..	3
3.	С помощью критерия устойчивости Гурвица……………	4
4.	С помощью критерия устойчивости Рауса……………….	6
5.	С помощью критерия устойчивости Михайлова…………	7
6.	С помощью критерия устойчивости Найквиста………….	9
7.	По логарифмическим частотным характеристикам……….	11
8.	Меры по обеспечению устойчивости……………………….	13

Контрольная работа №2.

Задание на выполнение контрольной работы.

Вариант №1

Исследовать систему автоматического управления, представленную структурной схемой на устойчивость:

1. С помощью критерия устойчивости Гурвица

2. С помощью критерия устойчивости Рауса

3. С помощью критерия устойчивости Михайлова

4. С помощью критерия устойчивости Найквиста

5. По логарифмическим частотным характеристикам.

В случае, если система неустойчива, предложить меры по обеспечению устойчивости.

; ; ;

Решение:

Найдем передаточную функцию W(p).

где:

;

;

;

Подставив значения получим:

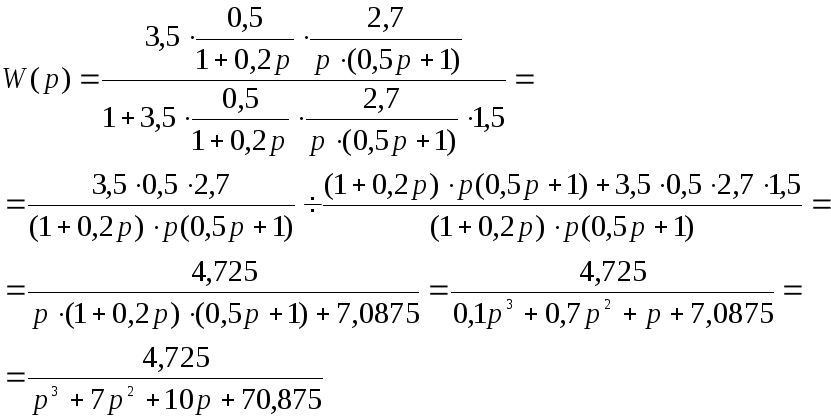
1. Исследуем систему на устойчивость с помощью критерия Гурвица.

Этот критерий является алгебраическим. Если задана передаточная функция системы W(p) = B(p) / A(p) , то для получения характеристического уравнения надо приравнять к нулю ее знаменатель

Порядок составления матрицы Гурвица следующий. В левом верхнем углу матрицы записывается коэффициент . По главной диагонали располагаются коэффициенты характеристического уравнения по мере убывания индексов. Над элементами главной диагонали записываются коэффициенты по убыванию индексов, под элементами - по возрастанию индексов. Там, где индекс больше n или меньше нуля, записываются нули.

Далее надо вычислить определители Гурвица, которые получают из матрицы путем отчёркивания равного числа строк и столбцов в левом верхнем углу матрицы.

Из коэффициентов характеристического уравнения составим сначала главный определитель Гурвица:

диагональные миноры:

.

< 0.

Критерий устойчивости Гурвица формулируется следующим образом: система устойчива, если все определители Гурвица больше нуля, т. е. Так как миноры матрицы меньше нуля, следовательно, система не устойчива.

2. Исследуем систему на устойчивость методом Рауса.

Составим таблицу:

В первой строке таблицы записываем в порядке возрастания индексов коэффициенты характеристического уравнения , имеющие четный индекс; а₀,а₂,а₄, и т.д.; во второй строке - коэффициенты характеристического уравнения , имеющие нечетный индекс; а₁,а₃,а₅.

		1	2
	1
	2
	3	с13 = а2 – r3а3= =-0,125
	4	с14 = а3 – r4с23= = 70,875

Из таблицы видно, что система будет неустойчивой, так как в колонке “1” есть отрицательное число, а именно с₁₃ = -0,125. А условие устойчивости Рауса формулируется так: для того, чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак.

3. Критерий устойчивости Михайлова

В отличие от алгебраического критерия Гурвица, этот критерий является частотным. Он основан на построении годографа характеристического вектора Годографом называется кривая, прочерчиваемая концом вектора на комплексной плоскости при изменении частоты от 0 до . Характеристический вектор получается из характеристического уравнения путем замены на .

Критерий устойчивости Михайлова формулируется следующим образом: система устойчива, если годограф характеристического вектора, начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении n квадрантов, где n - порядок характеристического уравнения системы.

Характеристический вектор можно представить в виде:

где - действительная, а - мнимая часть вектора

Действительная часть:

_{Корни уравнения:}

Мнимая часть:

V = - 1w³ + 10w = -w(1 w² -10)

-w(1 w² - 10) = 0

_{Корни уравнения:}

w₃ = 0.

Годограф Михайлова.

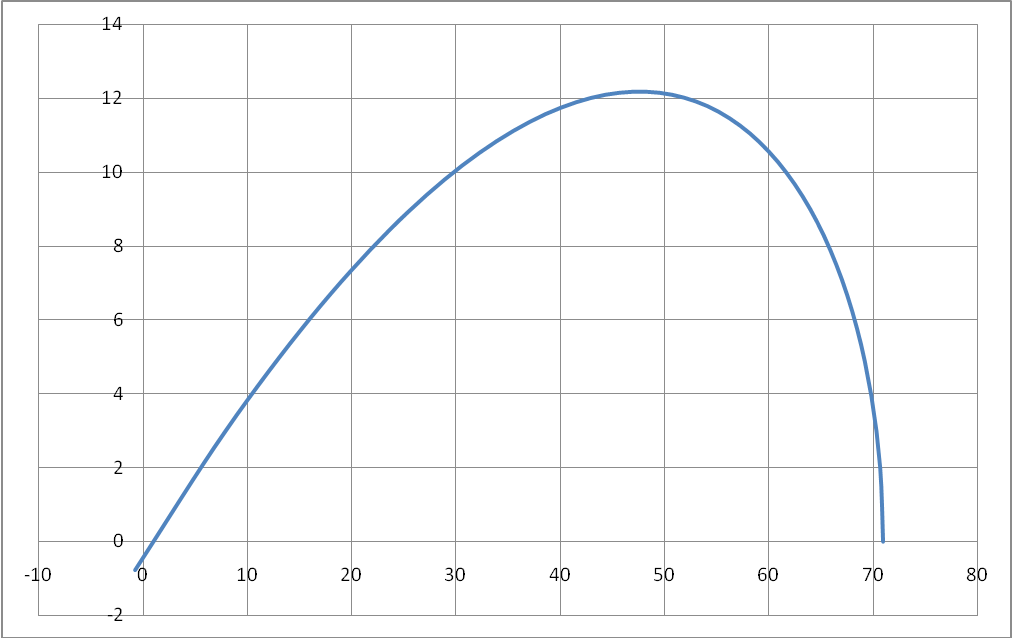
Система не устойчива.

С помощью критерия устойчивости Найквиста

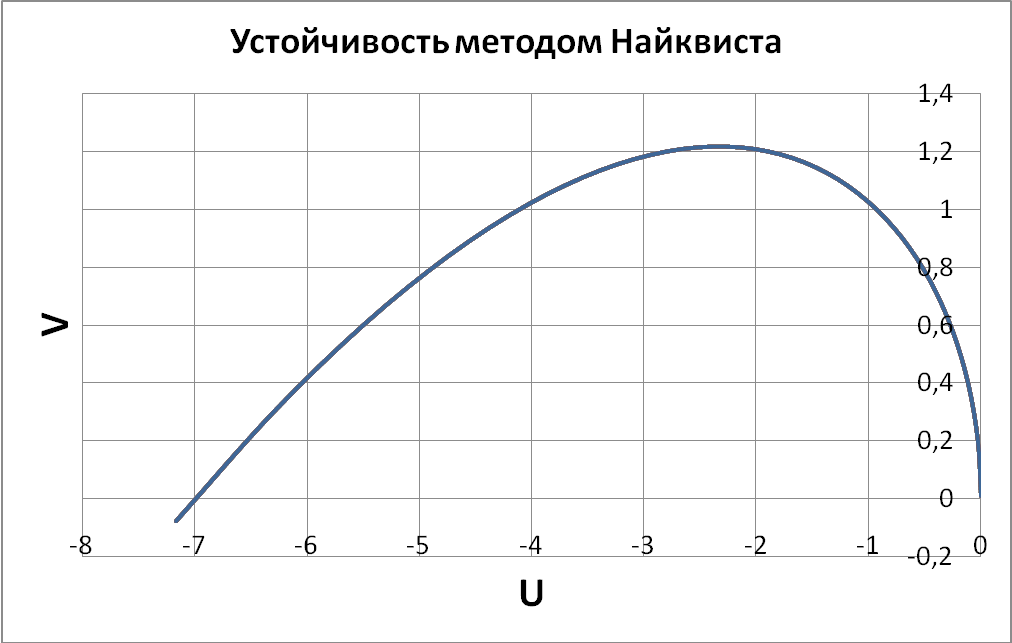
Критерий устойчивости Найквиста - один из способов судить об устойчивости замкнутой системы управления - по её разомкнутой АФЧХ. Является одним из частотных критериев устойчивости. С помощью этого критерия оценить устойчивость весьма просто, без необходимости вычисления полюсов передаточной функции замкнутой системы.

Так же, как и критерий Михайлова, критерий Найквиста является частотным. Он основан на построении годографа передаточной функции H(j) разомкнутой системы. Критерий устойчивости Найквиста формулируется следующим образом: замкнутая система устойчива, если годограф передаточной функции H(j) разомкнутой системы не охватывает на комплексной плоскости точку с координатами (-1, j0).

Вид разорванной предложенной системы,

Найдем передаточную функцию W(p).

Выделим мнимую и действительную части:

V = - 0,1jw³ +w

В результате получаем не устойчивую систему, так как кривая охватывает точку (-1;0).

Проверим разомкнутую систему на устойчивость методом Рауса.

Составим таблицу:

		1	2
	1
	2
	3	с13 = а2 – r3а3= =1
	4	с14 = а3 – r4с23= = 0

Так как С₁₃=0 система находится на границе устойчивости (неопределенная).

По логарифмическим частотным характеристикам

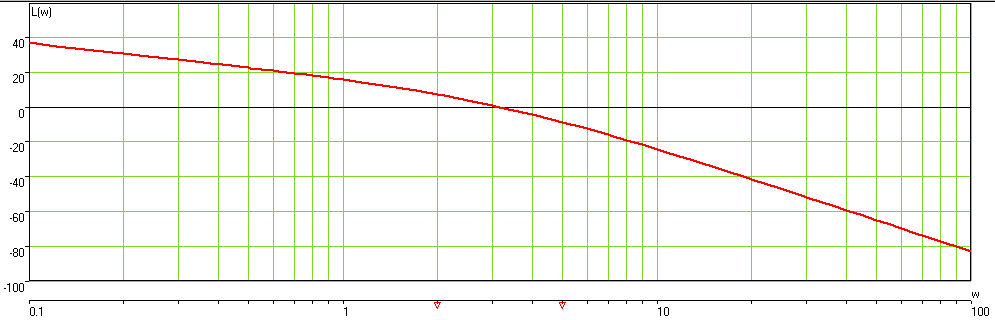
ЛАЧХ

ЛФЧХ

По разомкнутой системе передаточная функция:

;

_{У нас есть два элементарных звена. Постоим по ним логарифмические характеристики.}

lg0,3162=-0,5

1/Т = 1 lg 1= 0

Для построения ЛАЧХ воспользуемся следующей формулой:

L(ω)=20*Lg[A(ω)]

Амплитуда A(ω) рассчитывается следующим образом:

_{Из уравнения:}

Вещественная часть: Комплексная часть:

V = - 0,1jw³ +w

и

Система неустойчива, меры по обеспечению устойчивости:

Один из вариантов – это уменьшить значение до 0,5 и произвести проверку на устойчивость.

Проверку произведем одним из методов:

Проверим систему на устойчивость методом Рауса.

Заменим значение на 0,5 и произведем вычисление передаточной функции, получим:

Составим таблицу:

В первой строке таблицы записываем в порядке возрастания индексов коэффициенты характеристического уравнения , имеющие четный индекс; а₀,а₂, во второй строке - коэффициенты характеристического уравнения , имеющие нечетный индекс; а₁,а₃.

		1	2
	1
	2
	3	с13 = а2 – r3а3= =0,856225
	4	с14 = а3 – r4с23= = 1,0125

Условие устойчивости Рауса формулируется так: для того, чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот же знак.

Мы получили в колонке «1» все положительные знаки, а следовательно система автоматического управления устойчива.