РГР / raschet_slozhnoy_cepi_postoyannogo_toka_variant_12

Министерство образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Кафедра Теоретические Основы Электроники

Расчетно-графическая работа №1

на тему: расчет сложной электрической

цепи постоянного тока

Выполнил:

студент группы МКС-220

Хасаншин В.Р.

Проверила:

Медведева Л.С.

Уфа 2008

Задание:

1. Согласно индивидуальному заданию, составить схему электрической цепи.

2. Нарисовать ориентированный граф схемы.

3. Составить топологические матрицы схемы: соединений А, главных контуров В, главных сечений Q.

4. Проверить соотношения: АВ^Т = 0, QB^Т = 0.

5. Составить уравнения по законам Кирхгофа в алгебраической и матричной формах.

6. Определить токи в ветвях схемы методом контурных токов.

7. Определить токи в ветвях схемы методом узловых потенциалов.

8. Проверить правильность расчетов по законам Кирхгофа.

9. Составить баланс мощностей.

10. Для контура, содержащего две ЭДС составить потенциальную диаграмму.

11. Для ветви с сопротивлением R₁ определить ток методом эквивалентного генератора.

Вариант № 12.

1. Схема электрической цепи.

2. Ориентированный граф схемы.

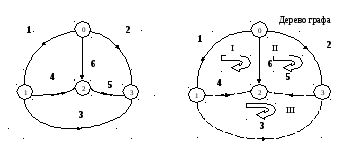
3. Топологические матрицы схемы

Матрица соединений А:

№ ветви № узла	1	2	3	4	5	6
1	1	0	-1	-1	0	0
2	0	0	0	1	1	1
3	0	1	1	0	-1	0

Матрица главных контуров В:

№ ветви № узла	1	2	3	4	5	6
1	-1	0	0	-1	0	1
2	0	1	0	0	1	-1
3	0	0	-1	1	-1	0

Матрица главных сечений Q:

№ ветви № узла	1	2	3	4	5	6
1	-1	0	1	1	0	0
2	0	0	0	-1	-1	-1
3	0	-1	-1	0	1	0

4. Проверим соотношения:

АВ^Т=0:

=

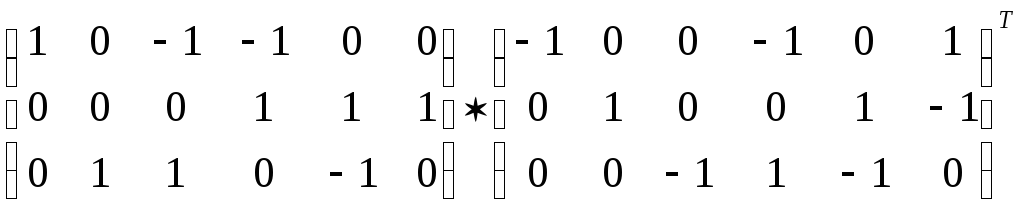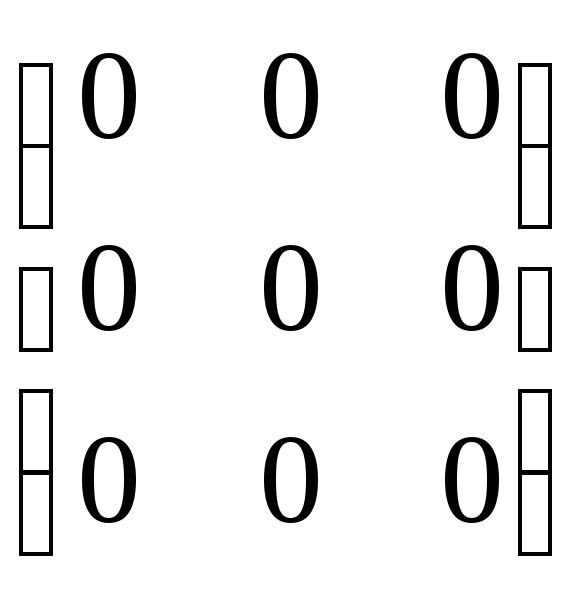
QB^Т = 0:

=

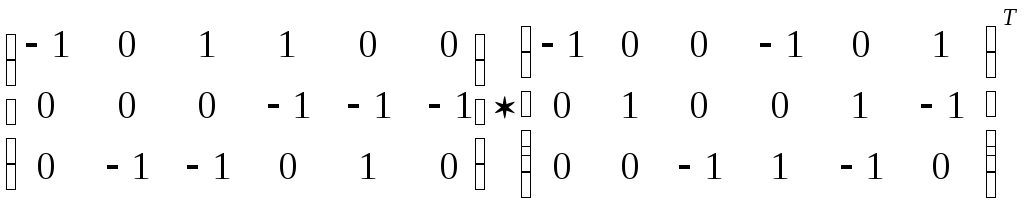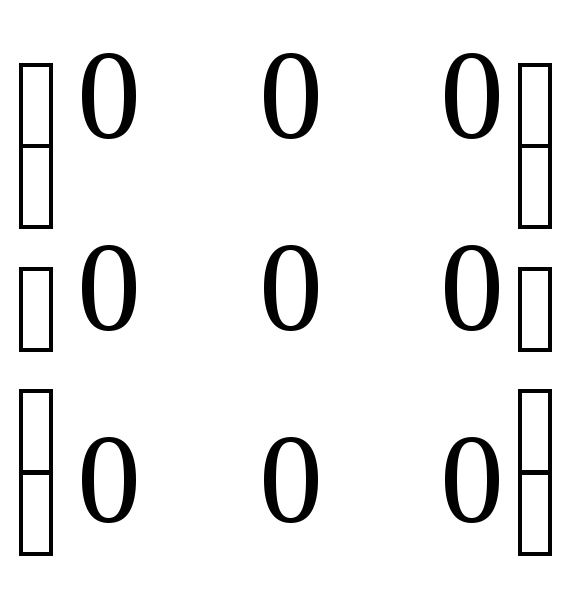
Равенство верно согласно приведенным вычислениям.

4. Уравнения по первому и второму законам Кирхгофа в матричной и алгебраической форме.

1. Первый закон Кирхгофа в матричной форме: АI = -AJ.

I = – матрица-столбец неизвестных токов;

J = – матрица-столбец источников токов.

= -

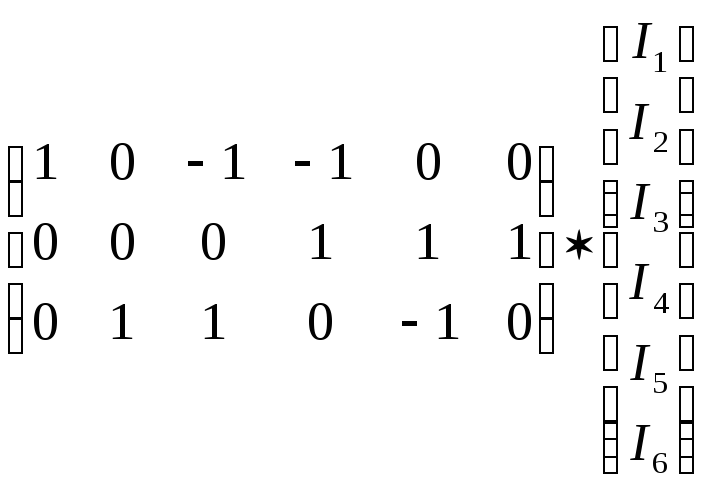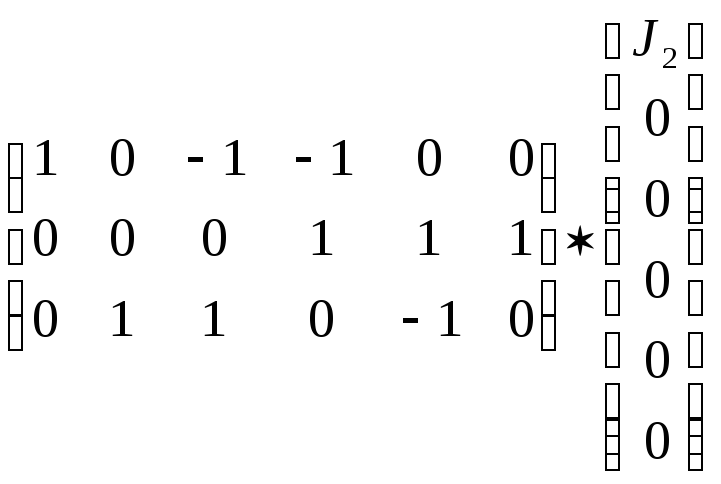
Перемножая соответствующие матрицы, получаем алгебраическую форму первого закона Кирхгофа:

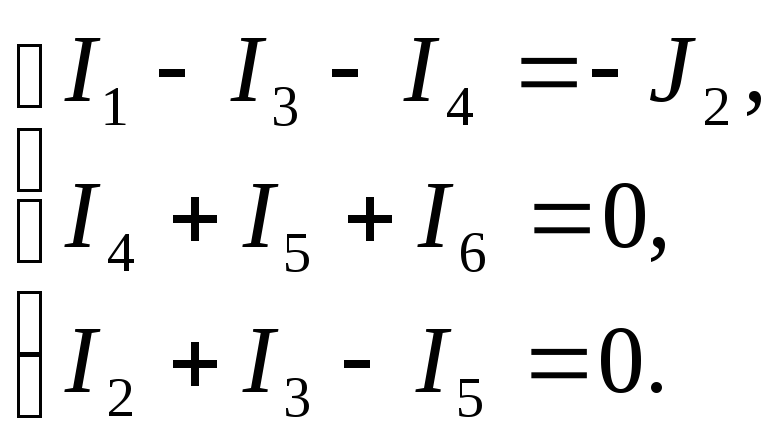
2. Второй закон Кирхгофа в матричной форме: BU = BE.

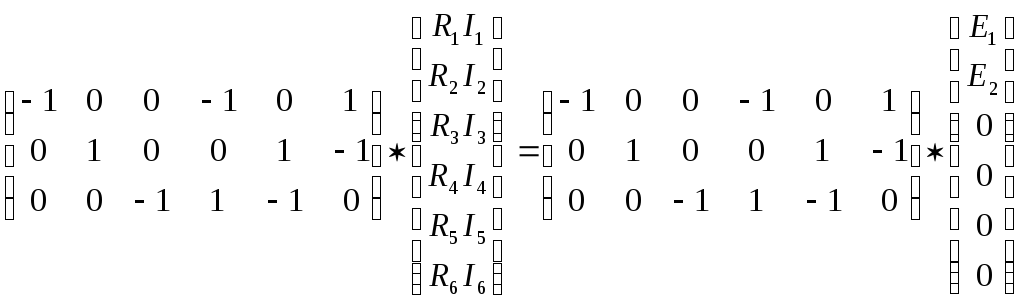
Перемножая соответствующие матрицы, получаем алгебраическую форму второго закона Кирхгофа:

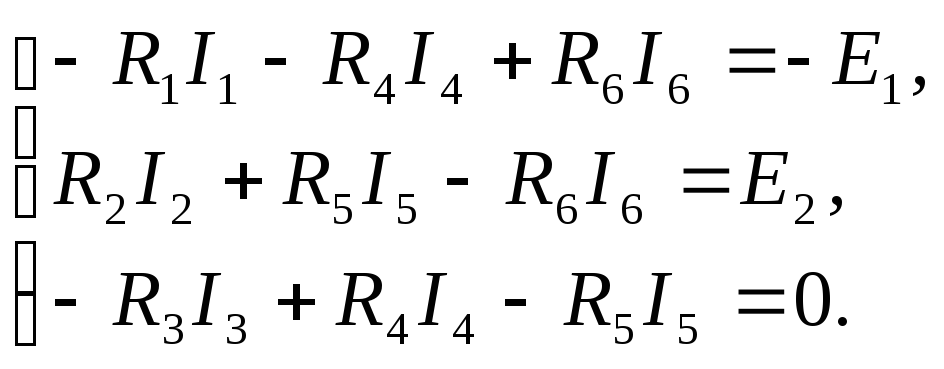
4. Определение токов в ветвях схемы методом контурных токов.

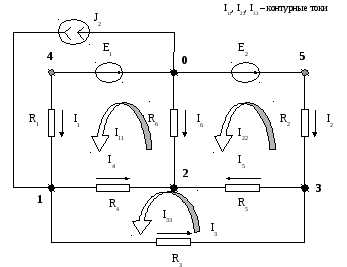
В матричной форме R_kkI_kk=E_kk.

I_kk – матрица-столбец неизвестных контурных токов:

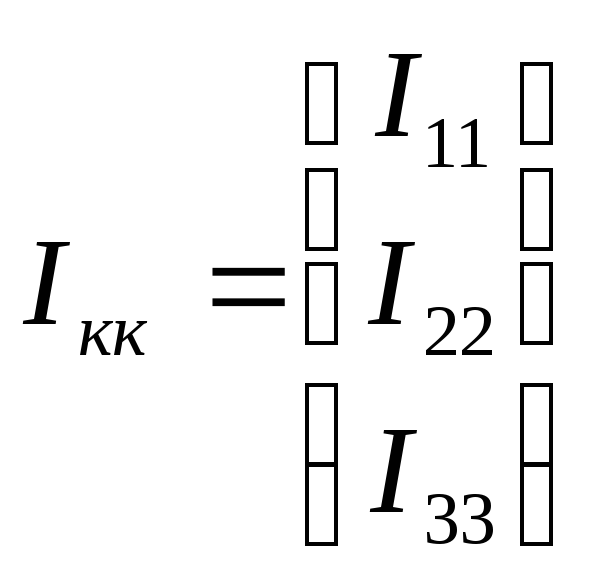
E_kk – матрица-столбец контурных ЭДС:

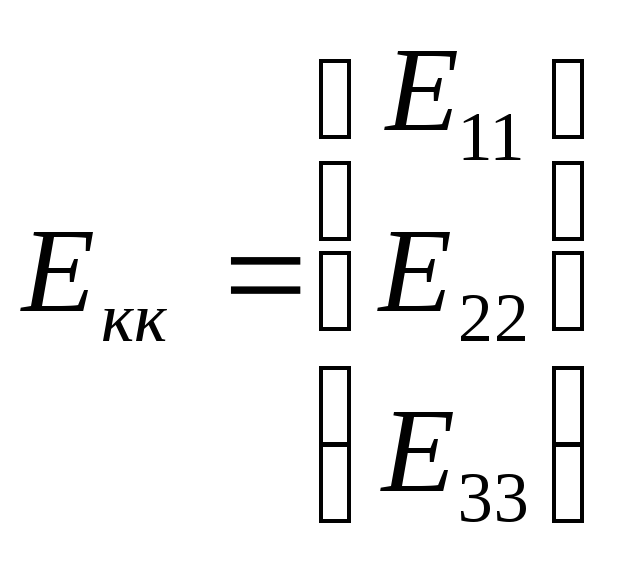
Собственные ЭДС контуров:

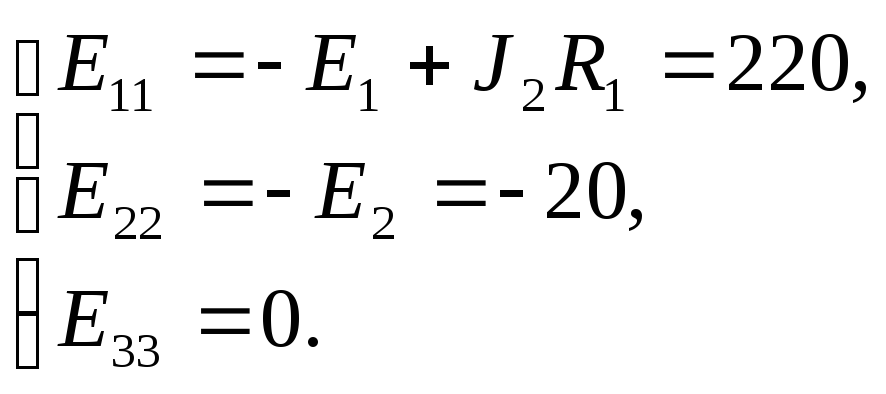
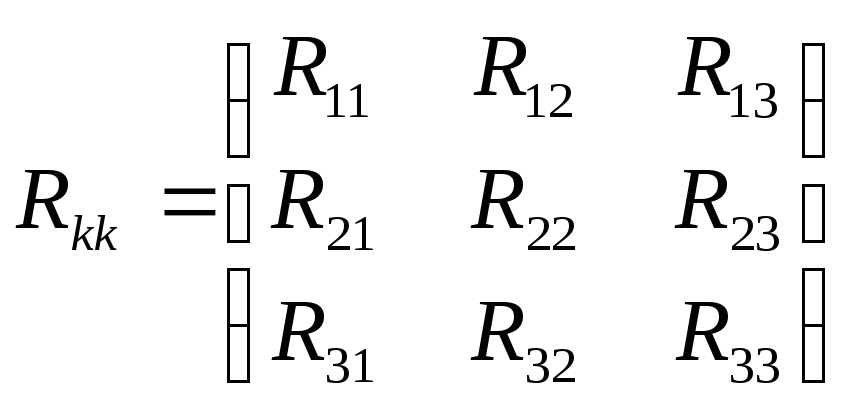
Матрица контурных сопротивлений:

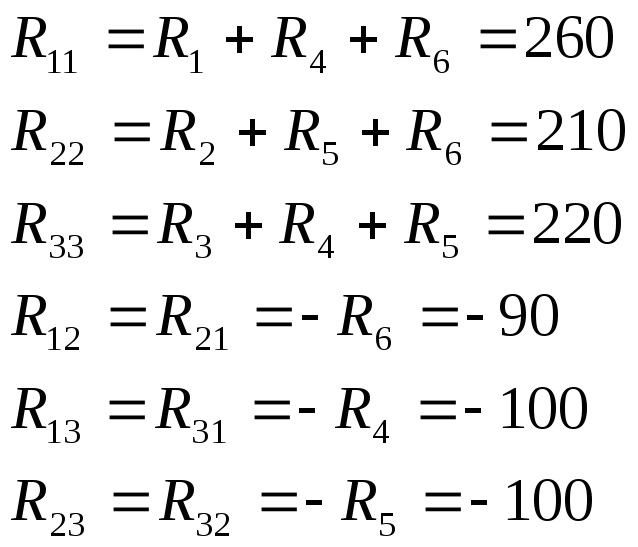
Подставим найденные значения в произведение R_kkI_kk=E_kk, получим систему уравнений:

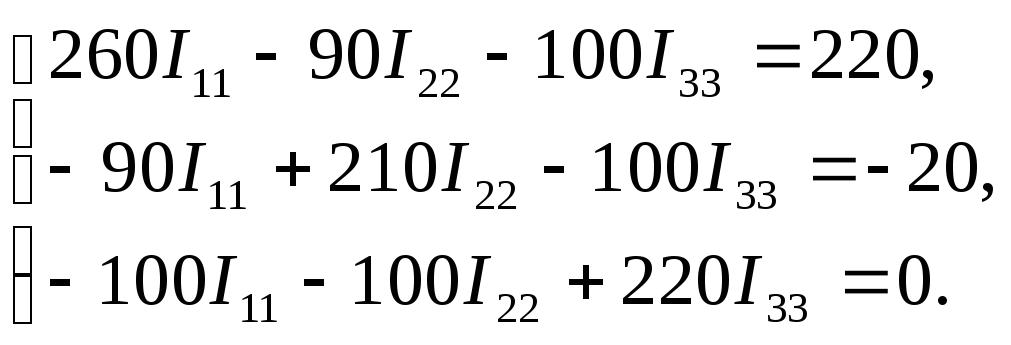
Решая систему методом Гаусса, получаем

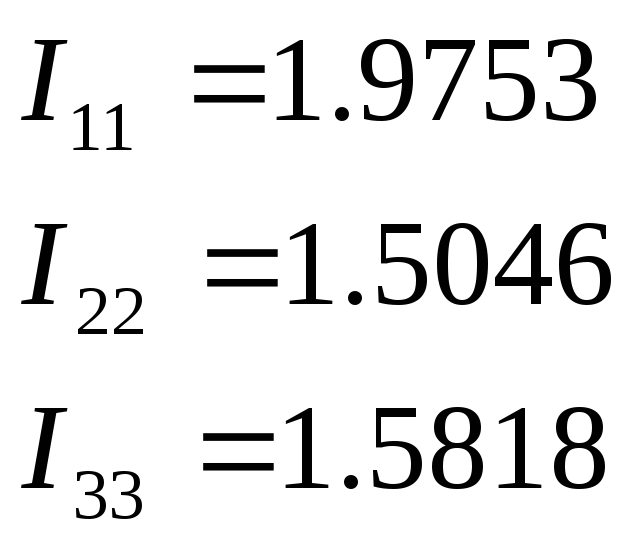
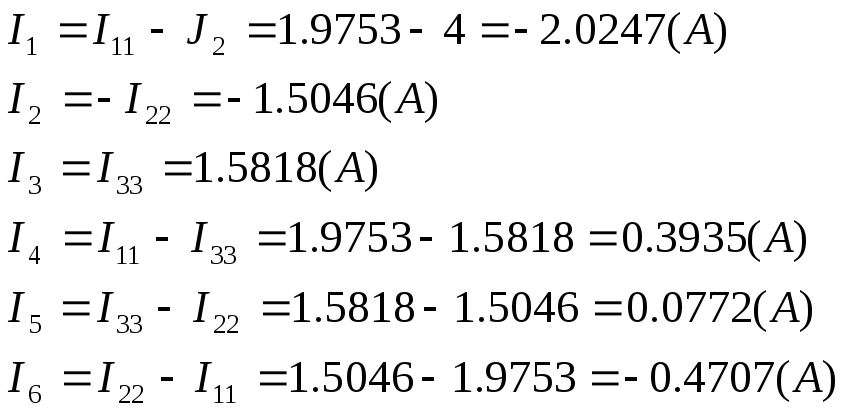
4. Определение токов в ветвях схемы методом узловых потенциалов.

Метод основан на I законе Кирхгофа и на обобщенном законе Ома.

Уравнение в матричной форме имеет вид: g_kkφ_kk=J_kk, где

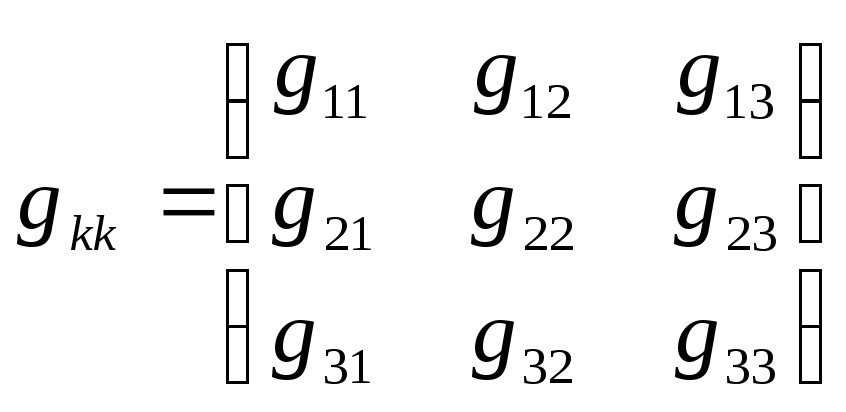– квадратичная матрица узловых проводимостей

– собственные проводимости узлов:

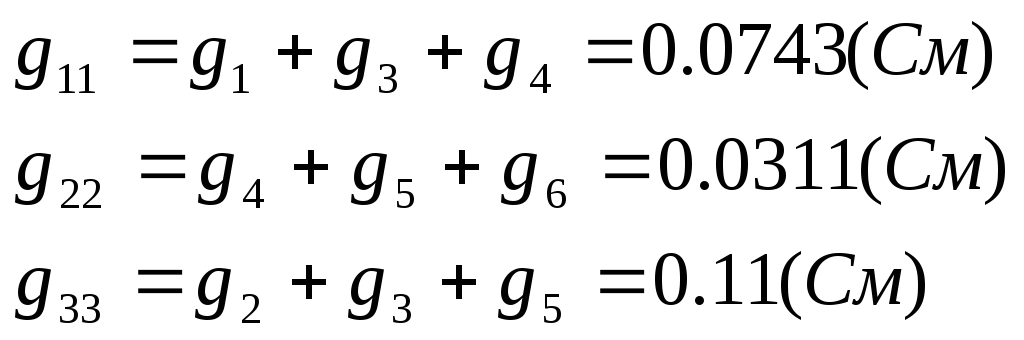
Взаимные проводимости:

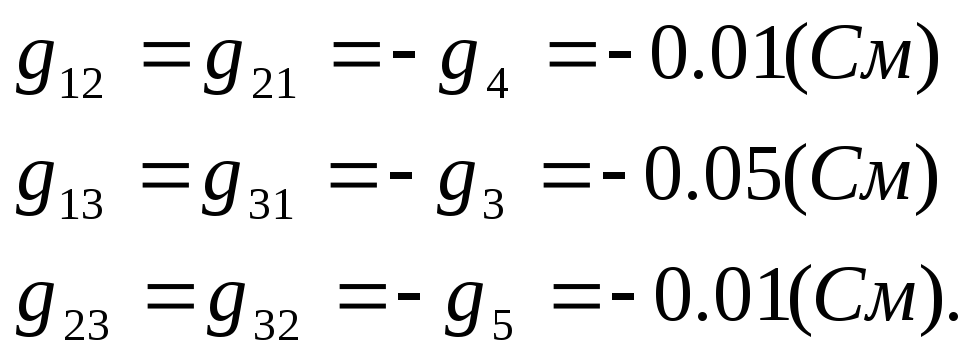
φ_кк – матрица-столбец неизвестных потенциалов:

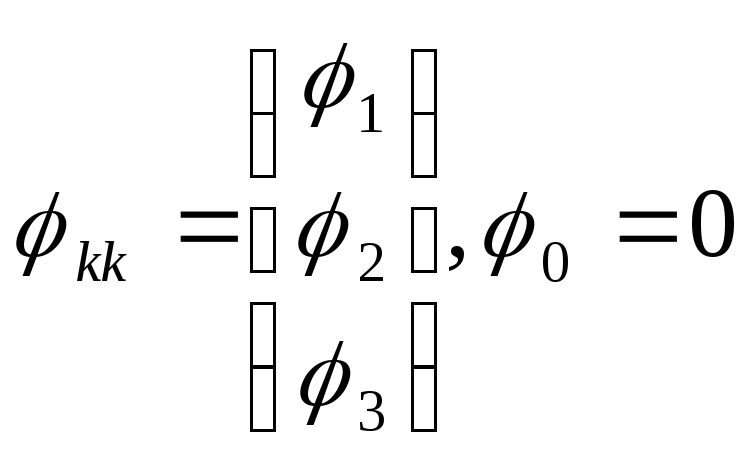
J_kk – матрица-столбец узловых токов:

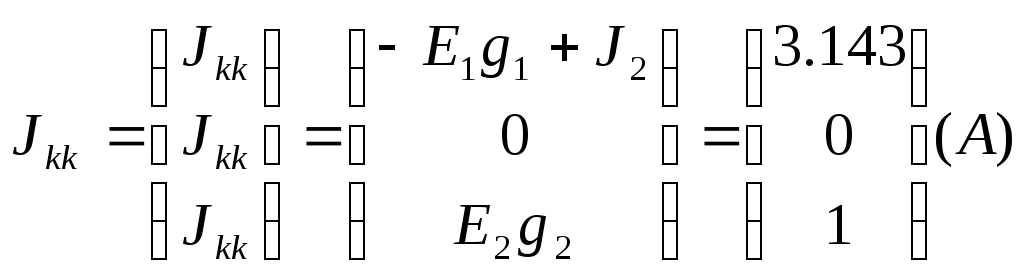
Подставляя значения в выражение g_kkφ_kk=J_kk, получим матрицу:

, решая методом Гаусса, получим:

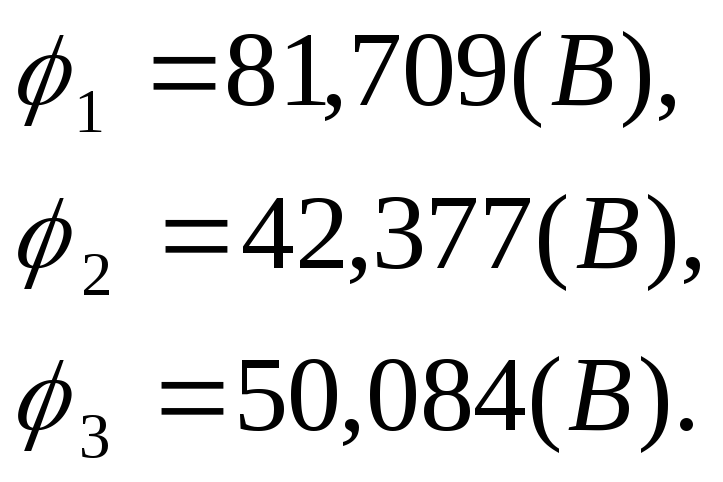
Истинные токи определяются по обобщенному закону Ома:

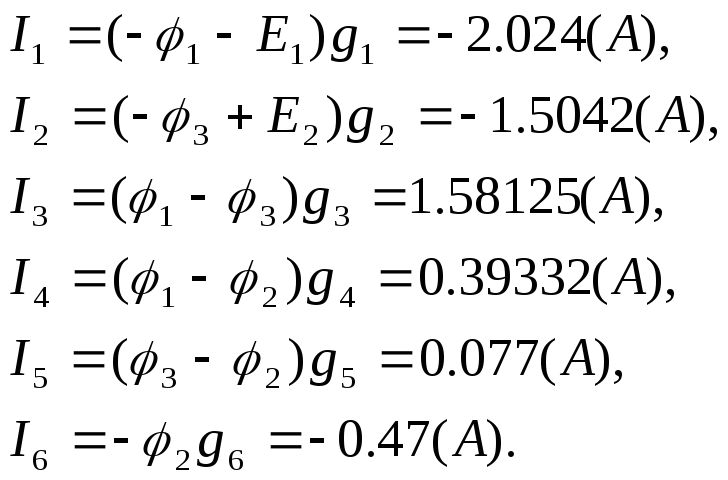
4. Проверка правильности расчетов по законам Кирхгофа.

Выше была получена система уравнений в алгебраической и матричной формах:

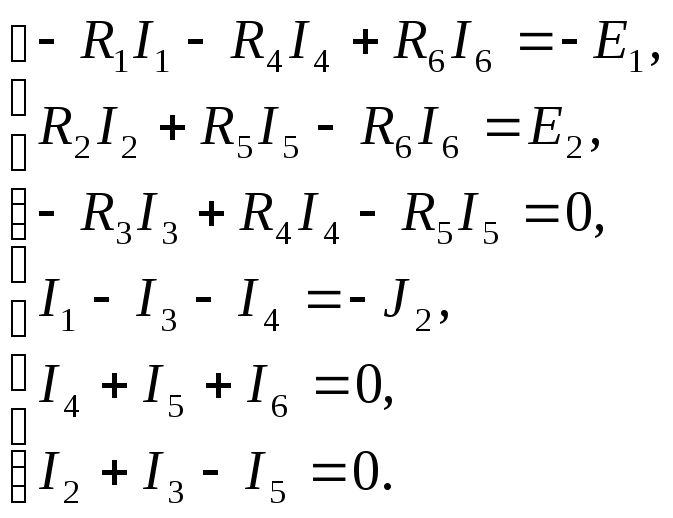
Получаем матрицу, которую решаем методом Гаусса:

Получаем:

Полученные значения совпадают со значениями, полученными с помощью методов МКТ и МУП, следовательно, расчеты верны.

4. Баланс мощностей.

Баланс мощностей является следствием закона сохранения энергии и является критерием проверки правильности полученных результатов.

Суммы в левой части равенства алгебраические, а сумма в правой – арифметическая.

Подставим значения в левую часть равенства:

Подставим значения в правую часть равенства:

Т.к значения левой и правой части равенства совпали в пределах погрешностей, то расчеты верны.

4. Потенциальная диаграмма для контура 0-5-3-1-4-0.

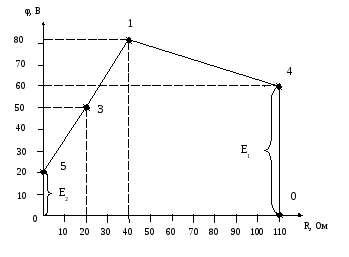
4. Расчет тока I₁ методом эквивалентного генератора.

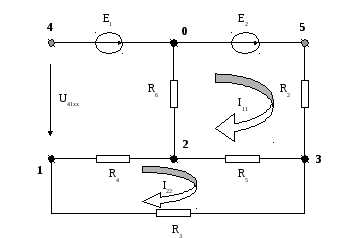
1. С помощью метода узловых потенциалов определим ЭДС генератора Е_Г.

Аналогично приведенному выше получаем:

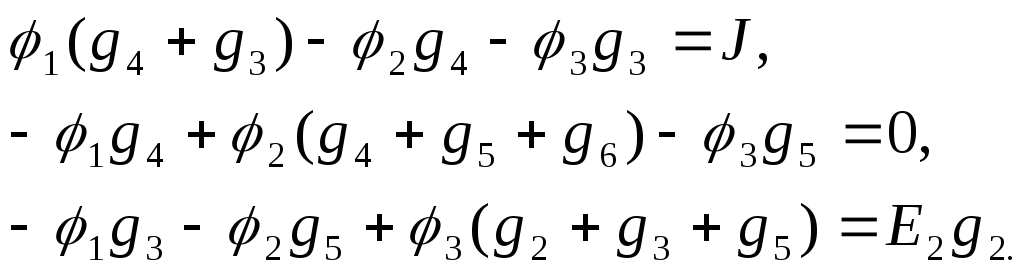
Подставляя значения, получаем матрицу, которую решаем методом Гаусса:

, получаем

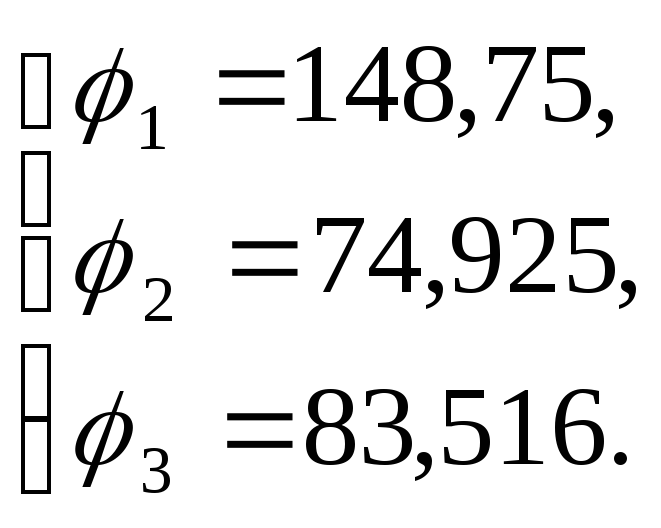
2. Определяем сопротивление генератора R_Г.

Для получения двухполюсника все источники ЭДС закорачиваем, все источники тока размыкаем.

Преобразовываем треугольник в звезду, получаем:

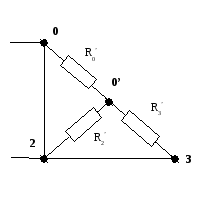
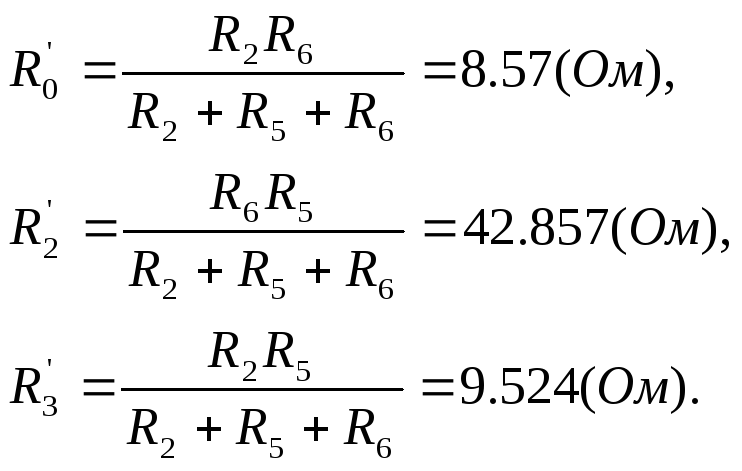
В результате преобразований получаем следующую цепь:

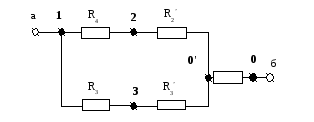
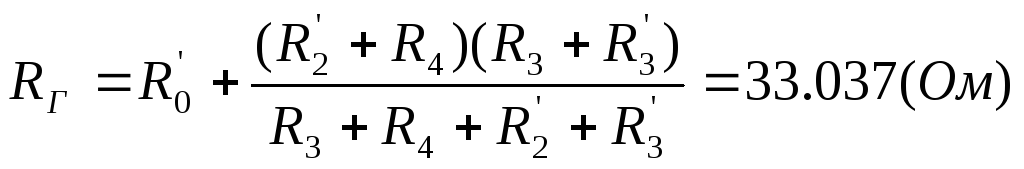
Ток вычислен методом эквивалентного генератора. Полученное значение совпадает с рассчитанным выше значением силы тока.

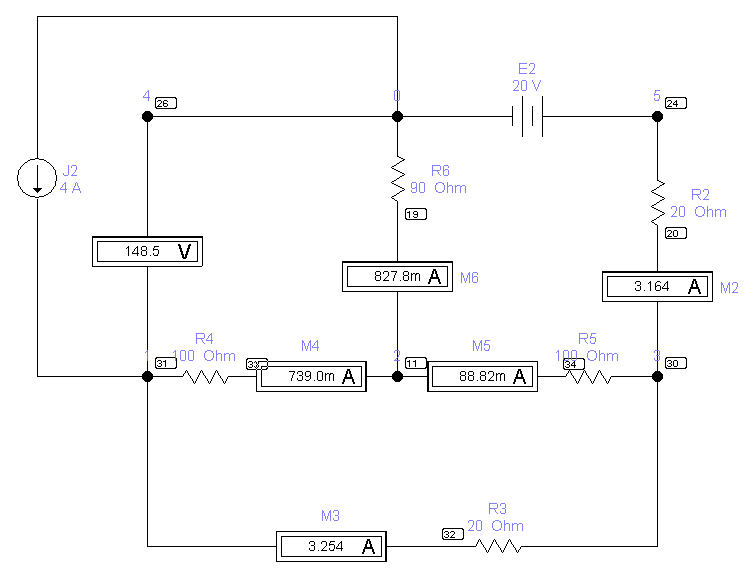
Схема со значениями токов, рассчитанными с помощью приложения Electronics Workbench (обозначения на схеме согласно версии 5.12) и истинными направлениями токов.

I₁

I₆

I₂

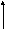
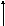
I₃

I₅

I₄

Схема со значениями тока короткого замыкания и напряжения холостого хода, рассчитанными с помощью приложения Electronics Workbench (обозначения на схеме согласно версии 5.12).

.

Вывод: в ходе расчетно-графической работы №1 мной был выполнен анализ электрической цепи постоянного тока и получены токи в ее ветвях различными методами: методом контурных токов, методом узловых потенциалов, методом эквивалентного генератора. Также была построена потенциальная диаграмма для контура, содержащего 2 ЭДС. Проверка правильности полученных токов была осуществлена с помощью законов Кирхгофа и баланса мощностей. Существует некоторая погрешность, обусловленная неточностью вычислений (последовательные округления и т.п.). В результате использования трех методов получились одинаковые токи, так как ток в цепи не зависит от способа решения.