
- •6. Формирование оптического излучения
- •6.1. Формирование микрорельефа в резисте
- •6.2. Системы экспонирования
- •6.3. Основы теории формирования микроизображений
- •Волновые процессы в оптике
- •Представление волн в векторном и комплексном виде
- •6.4. Скалярная теория дифракции Уравнение Гельмгольца
- •Теорема Грина
- •Интегральная теорема Гельмгольца — Кирхгофа
- •Применение интегральной теоремы
- •Граничные условия Кирхгофа
- •Формула дифракции Френеля — Кирхгофа
- •Формула дифракции Рэлея — Зоммерфельда
- •Приближение Кирхгофа
- •Приближение Френеля
- •Дифракция при контактной фотолитографии
- •Расчет распределения интенсивности
- •Контрольные вопросы и задания
- •7. Проекционное формирование микроизображений
- •7.1. Качество проекционного изображения
- •7.2. Понятие изображающей системы
- •7.3. Связь между объектом и изображением
- •7.4. Свертка
- •7.5. Фурье-преобразования в оптике Понятие пространственной частоты
- •Ряды Фурье
- •Ряд Фурье в комплексной форме
- •Интеграл Фурье
- •Фурье-преобразование
- •Фурье-преобразование изображения
- •7.6. Оптическая передаточная функция
- •7.7. Зрачковая функция и ее связь с оптической передаточной функцией
- •7.8. Связь комплексной амплитуды изображения со зрачковой функцией
- •7.9. Оптическая передаточная функция как автокорреляция зрачковой функции
- •7.10. Системы дифракционного качества с постоянным пропусканием по площади зрачка
- •7.11. Учет распределения интенсивности в изображении
- •Контрольные вопросы и задания
7.11. Учет распределения интенсивности в изображении
Распределение интенсивности в изображении, создаваемом оптической системой, можно найти при использовании фурье-преобразований функций, входящих в интеграл свертки. В результате получаются соответственно частотное распределение интенсивности в объекте и оптическая передаточная функция. Простое перемножение этих функций позволяет получить частотное распределение интенсивности в изображении. Применив к нему обратное фурье-преобразование, можно найти искомое распределение интенсивности в изображении.
Каждая косинусоидальная составляющая пространственного распределения в объекте преобразуется в изображение без изменений ее частоты, меняются только амплитуда и фаза этой составляющей.
Для случая дифракционно-ограниченной системы, когда волновые аберрации отсутствуют, может быть предложена следующая процедура.
1. Для известного (заданного) пространственного распределения интенсивности Io(x) в объекте находят частотное распределение объекта Io(ν) с помощью фурье-преобразования:
![]() (7.78)
(7.78)
Результатом является частотный спектр объекта, то есть набор значений коэффициентов Фурье для различных гармоник, описывающих заданный профиль распределения интенсивности в объекте.
2. Рассчитывают частотное распределение изображения Ii(ν). Для этого частотное распределение объекта умножают на коэффициент передачи модуляции:
![]() (7.79)
(7.79)
Предварительно для каждой частоты рассчитывают соответствующее значение T(), далее умножают его на значение коэффициента Фурье соответствующей гармоники.
3. Находят пространственное распределение интенсивности в изображении за счет обратного фурье-преобразования:
![]() (7.80)
(7.80)
Полученные в (7.79) новые значения коэффициентов Фурье используются для воссоздания соответствующих гармоник разложения. Суммирование значений гармоник для текущей координаты профиля позволяет получить значение интенсивности в изображении для данной координаты.
4. Оценивают распределение интенсивности в изображении с технологической точки зрения. Дифракционное размытие изображения приводит к тому, что на участки фоторезиста, лежащие в области геометрической тени, попадает часть экспонирующего излучения. Получаемая этими участками доза экспозиции может стать достаточной для утонения фоторезиста, в результате он не сможет служить защитной маской при последующих операциях.
Деструкция фоторезиста в затененных участках будет зависеть не только от степени размытия изображения, но и от контраста самого фоторезиста, который часто выражается через его модуляцию.
Для получения
микрорельефа в фоторезисте необходимо,
чтобы модуляция оптического изображения
превышала модуляцию фоторезиста, т. е.
чтобы выполнялось условие T > Tf.
У фоторезистов, согласованных с
источниками излучения в диапазоне линий
g, h, i, контраст составляет
= 2...3, при этом согласно формуле (7.2)
модуляция равна Tf =
0,36...0,70. Поэтому на значение опического
контраста накладывается ограничение
![]() .
.
Как следует из рис. 7.12, изображение с высоким оптическим контрастом имеет меньший клин проявления. Показанное пунктиром уменьшение разности между E1 и E0 (дозы начала и полного проявления фоторезиста) также делает изображение более резким.
Таким образом, контраст (модуляция) оптического изображения и контраст фоторезиста определяют разрешение всего литографического процесса. Поэтому для полученного распределения интенсивности в изображении необходимо оценить его контраст, сравнить с требуемым контрастом и вынести решение о возможности получения заданного изображения в данной литографической системе.
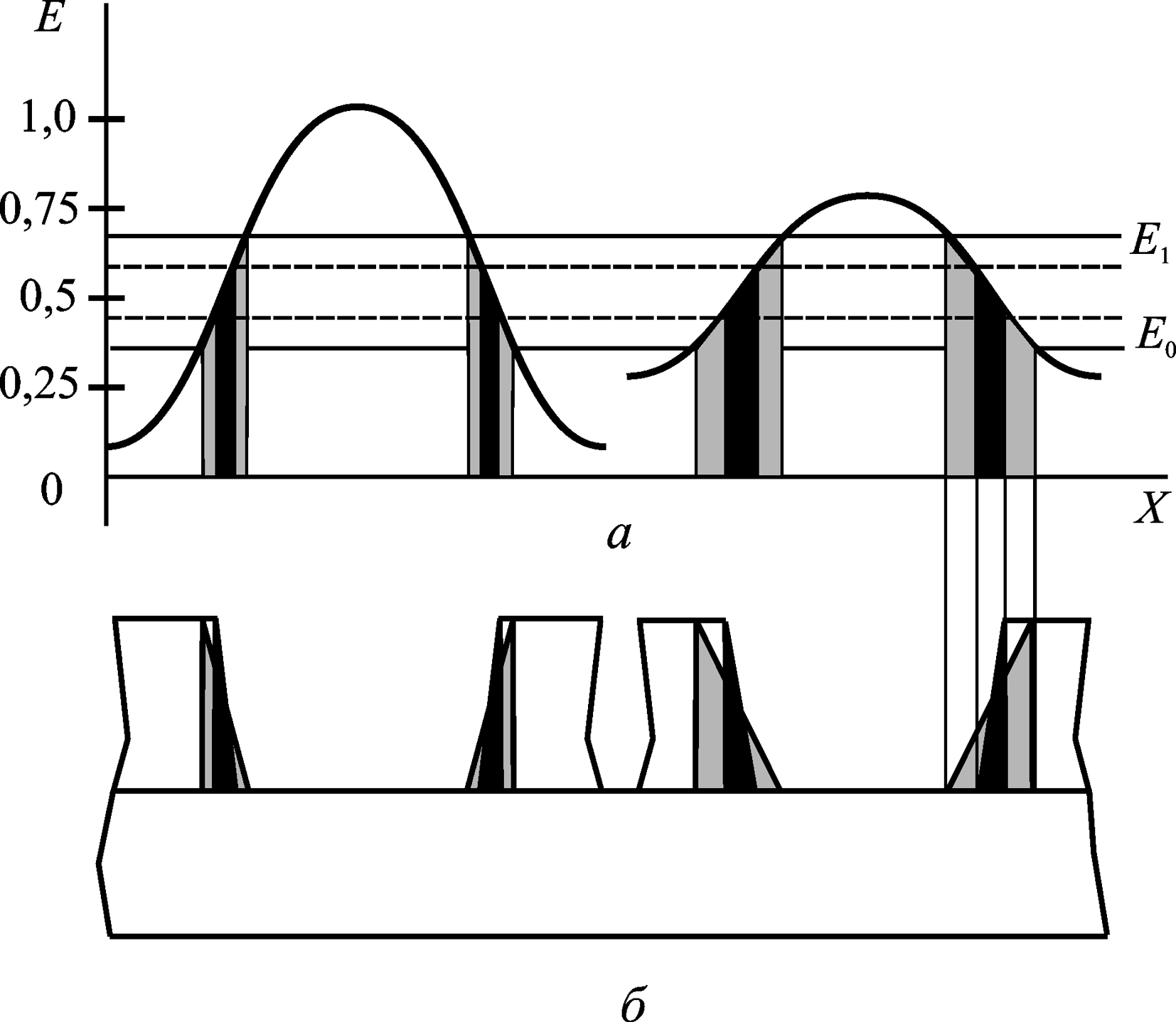
Рис. 7.12. Влияние параметров изображения и фоторезиста на качество микрорельефа:
а — контрасты изображения и фоторезиста; б — клин проявления
