- •Рецензенты:
- •Содержание
- •Предисловие
- •Учебно-тематический план
- •Разработки занятий Лабораторное занятие №1 Тема занятия «Определение и способы задания функции. Элементарные функции»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Примеры решения типовых задач
- •Найдите область определения функции:
- •3. Исследуйте функции на четность:
- •Определите нули и промежутки знакопостоянства функции:
- •Выделите промежутки, на которых существуют обратные функции для функции и найдите их.
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Примеры решения типовых задач
- •7. Вычислите односторонние пределы:
- •Практические задания для развития и контроля владения компетенциями Задания, решаемые в аудитории
- •Задания для самостоятельной работы дома
- •Лабораторное занятие №3 Тема занятия «Понятие производной. Правила дифференцирования»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Примеры решения типовых задач
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Примеры решения типовых задач
- •Практические задания для развития и контроля владения компетенциями Задания, решаемые в аудитории
- •Задания для самостоятельной работы дома
- •Лабораторное занятие №5 Тема занятия «Первообразная функция, неопределенный интеграл и его свойства. Методы интегрирования»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Примеры решения типовых задач
- •Практические задания для развития и контроля владения компетенциями Задания, решаемые в аудитории
- •Задания для самостоятельной работы дома
- •Лабораторное занятие №6 Тема занятия «Понятие определенного интеграла. Интегрирование по частям и замена переменной в определенном интеграле»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Примеры решения типовых задач
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Примеры решения типовых задач
- •Практические задания для развития и контроля владения компетенциями Задания, решаемые в аудитории
- •Задания для самостоятельной работы дома
- •Лабораторное занятие №8 Тема занятия «Контрольная работа №1»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •II. Вопросы для подготовки к коллоквиуму №1 Тема «Дифференциальное и интегральное исчисления функции одной переменной»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Примеры решения типовых задач
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Лабораторное занятие №12 Тема занятия «Контрольная работа №2»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Лабораторное занятие №13 Тема занятия «Оценка параметров генеральной совокупности по случайной выборке»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Примеры решения типовых задач
- •Лабораторное занятие №14 Тема занятия «Определение параметров эмпирических формул. Точность и надежность оценки. Метод наименьших квадратов. Построение нормальной кривой по опытным данным»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Лабораторное занятие №15 Тема занятия «Линейная регрессия. Коэффициент корреляции»
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Вопросы, выносимые на обсуждение
- •Методические рекомендации
- •Рекомендуемая литература
- •Теоретические задания для развития и контроля владения компетенциями
- •Вопросы, выносимые на обсуждение
- •Учебно-методическое и информационное обеспечение дисциплины
Вопросы, выносимые на обсуждение
-
Применение определенного интеграла для вычисления площадей.
-
Вычисление длины дуги.
-
Вычисление объемов.
-
Вычисление площади поверхности вращения.
-
Приложения определенного интеграла к решению задач естествознания.
Методические рекомендации
Для подготовки к занятию дома
-
Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.
-
Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.
-
Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.
-
Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.
-
Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.
На занятии по указанию преподавателя
-
Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.
-
В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.
-
Разберите с преподавателем вопросы, которые остались Вами не понятыми по теме этого занятия.
Дома закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома. В тетради для индивидуальных домашних заданий выполните ИДЗ №3 по теме «Основные методы интегрирования. Приложения определенного интеграла» и сдайте на следующем занятии выполненное задание на проверку преподавателю.
Рекомендуемая литература
[1] глава 9 пп 9.10 - 9.11.
[4] глава X §§ 3 – 9.
[5] глава 8 §§ 45 – 46.
[6] часть III занятия 15 – 16.
[7] глава 5 § 5.6.
[8] глава 8 § 10.
[9] глава VIII §10.
[10] глава 6 § 11.
Теоретические задания для развития и контроля владения компетенциями
1. Подготовьтесь к самостоятельной работе №4 по теме «Определенный интеграл». Примерный вариант можете найти в программе дисциплины.
2. Что называется площадью плоской фигуры? 3. Как найти площадь плоской фигуры с помощью определенного интеграла?
4. Дайте определение полярной системы координат. Установите формулы, связывающие полярные и прямоугольные координаты точки.
5. Запишите формулу для вычисления площади плоской фигуры в полярных координатах.
5. Что называется объемом тела? Как найти объем тела вращения?
7. Что называется длиной дуги?
8. Как найти длину дуги: если функция задана:
а) в декартовых координатах?
б) в полярных координатах?
в) параметрически?
9. Какие еще приложения определенных интегралов Вы знаете?
10. Разберите примеры решения типовых задач в тетради.
Примеры решения типовых задач
1.
Вычислите площадь, ограниченную
параболами
![]() и
и
![]()
Решение.
Определим
точки пересечения парабол и построим
эти параболы:
![]() отсюда,
отсюда,
![]() - абсциссы точек пересечения.
- абсциссы точек пересечения.
Ординаты
точек пересечения находим, подставляя
найденные абсциссы в уравнение одной
из парабол:
![]()
![]() и
и
![]() - точки пересечения парабол.
- точки пересечения парабол.

Из
рисунка видим, что площадь искомой
фигуры
![]()


Площадь
ОВD
расположена под осью
![]() ,
поэтому перед знаком интеграла берем
знак «минус».
,
поэтому перед знаком интеграла берем
знак «минус».

Отсюда
![]()
2.
Найдите площадь одного лепестка кривой
![]()
Решение.
Один лепесток
кривой получаем при изменении
![]() от 0 до
от 0 до
![]() .
По формуле вычисления площади в полярных
координатах имеем
.
По формуле вычисления площади в полярных
координатах имеем

![]()
Применяя формулы тригонометрии, имеем:
![]()
![]()
Отсюда
![]()
![]()
3.
Найти объем тела, образованного вращением
фигуры, ограниченной одной полуволной
синусоиды
![]() ,
прямой
,
прямой
![]() вокруг оси
вокруг оси
![]()

Решение. Объем
тела вращения, образованного вращением
кривой вокруг оси
![]() ,
определяется формулой:
,
определяется формулой:

4.
Найти объем тела, полученного вращением
вокруг оси
![]() плоский фигуры, ограниченной аркой
циклоиды
плоский фигуры, ограниченной аркой
циклоиды
![]()
![]()
Решение.
Объем тела
вращения, образованного вращением
кривой вокруг оси![]() :
:
![]()
Пользуясь
данными параметрическими уравнениями
циклоиды, преобразуем интеграл к
переменной
![]() тогда
тогда
![]() при
при
![]() при
при
![]()
Тогда
![]()

5.
Найдите длину дуги полукубической
параболы
![]() от начала координат до точки
от начала координат до точки
![]()

Решение. Для вычисления длины дуги в прямоугольной декартовой системе координат воспользуемся формулой:

Разрешим
данное уравнение кривой относительно
![]() и
находим
и
находим
![]()
![]()
(Знаки
![]() в выражении
в выражении
![]() указывают ,что кривая симметрична
относительно оси
указывают ,что кривая симметрична
относительно оси
![]() ).
).
Тогда


6.
Найдите длину астроиды
![]()
Решение. Длина дуги кривой, заданной параметрически, вычисляется по формуле:
![]() где
где
![]() .
.
Найдем
![]() и
и
![]()
Учитывая
симметричность астроиды, найдем длину
ее дуги при изменении
![]() от 0 до
от 0 до
![]() (длина дуги, расположенной в 1 четверти).
Тогда длина всей дуги
(длина дуги, расположенной в 1 четверти).
Тогда длина всей дуги
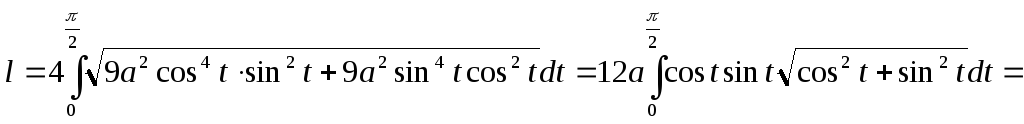

7.
Скорость роста некоторой популяции
микроорганизмов подчинена закону
![]() где
где
![]() время в секундах. Найдите численность
этой популяции в момент времени
время в секундах. Найдите численность
этой популяции в момент времени
![]() ,
если численность этой популяции в момент
времени 30с была 100000 единиц.
,
если численность этой популяции в момент
времени 30с была 100000 единиц.
Решение.
Так как скорость роста популяции
![]() является производной от численности
популяции
является производной от численности
популяции
![]() ,
следовательно, численность популяции
,
следовательно, численность популяции
![]() является первообразной для
является первообразной для
![]() .
Поэтому
.
Поэтому
 или
или

Тогда