1)Свет как электромагнитная волна

свет – волны, распространяющиеся в особой среде – эфире, заполняющем все

пространство.

Во второй половине XIX века Максвелл показал, что свет –

частный случай электромагнитных волн. Эти работы послужили фундаментом для

электромагнитной теории света. Однако в начале XX века было обнаружено, что при

излучении и поглощении свет ведет себя подобно потоку частиц.

Монохроматическая волна

Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени.

Монохроматическая волна – такая синусоида бесконечной длины – это, конечно, чистая абстракция. Нигде никогда таких волн не бывает.

Волновой цуг (пакет)

Беря суперпозицию синусоидальных волн, мало отличающихся друг от друга по частотам , можно построить, так называемый, волновой пакет, то есть пакет с определённой длиной волны Δx и определённой длительностью Δt.2) Значит, можно получить такое решение [уравнения Шрёдингера], которое называется волновым пакетом. Он ограничен в пространстве и во времени.

 

Синусоидальная волна имеет скорость, называемую фазовой, . Волновой пакет строится из набора волн с частотами в интервале  и волновыми числами . Скорость электромагнитной волны в вакууме не зависит от частоты, но, если есть дисперсия, скорость зависит от частоты. В диспергирующей среде волновой пакет расплывается, поскольку скорости его монохроматических составляющих отличаются друг от друга, весь пакет идёт с групповой скоростью

Свечение тел объясняется испусканием света атомами или молекулами вещества, поскольку последние могут быть промоделированы как системы ускоренно движущихся друг относительно друга положительных и отрицательных зарядов. Движение зарядов предполагается колебательным. В его процессе энергия атома переходит в энергию излучения, поэтому колебания являются затухающими, и поле сферической волны, испускаемой отдельным атомом, имеет вид волнового цуга

Ограниченный ряд повторяющихся возмущений называется цугом

распространяющееся волновое поле, занимающее в каждый момент времени ограниченную область пространства. В. п. может возникнуть у волн любой природы (звуковых, электромагнитных и т.п.). Такой волновой "всплеск" в некоторой области пространства может быть разложен на сумму монохроматических волн, частоты которых лежат в определённых пределах

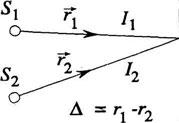
2)Интерференция 2-х монохроматических волн

В идеальном случае монохроматических источников при наложении двух пучков света с интенсивностями и распределение интенсивности в интерференционной картине описывается формулой:

(1.1)

где – разность хода интерферирующих волн, 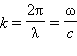– волновое число.

Рисунок 1.1. Интерференция волн от двух точечных монохроматических источников.

Характер наблюдаемой интерференционной картины зависит от взаимного расположения источников и и плоскости наблюдения P (рис. 1.1). Интерференционные полосы могут иметь, например, вид семейства концентрических колец или гипербол. Наиболее простой вид имеет интерференционная картина, полученная при наложении двух плоских монохроматических волн, когда источники и находятся на достаточном удалении от экрана. В этом случае интерференционная картина имеет вид чередующихся темных и светлых прямолинейных полос (интерференционные максимумы и минимумы), расположенных на одинаковом расстоянии друг от друга.

Когерентность

(от латинского cohaerens — находящийся в связи), согласованное протекание во времени нескольких колебательных или волновых процессов, проявляющееся при их сложении. Колебания называются когерентными, если разность их фаз остаётся постоянной во времени и при сложении колебаний определяет амплитуду суммарного колебания. Два гармонических (синусоидальных) колебания одной частоты всегда когерентны

3)оптическая длина пути

Оптическая длина пути, оптический путь, между точками А и В прозрачной среды; расстояние, на которое свет (оптическое излучение) распространился бы в вакууме за время его прохождения от А до В. Поскольку скорость света в любой среде меньше его скорости в вакууме, О. д. п. всегда больше реально проходимого светом расстояния (или, в предельном случае вакуума, равна ему). В оптической системе, состоящей из р однородных сред (траектория луча света в такой системе — ломаная линия), О. д. п. равна , где l_k — расстояние, пройденное светом в k-той среде (k = 1, 2,..., р), n_k — показатель преломления этой среды,  — знак суммы. Для одной среды (р = 1) сумма сокращается до единственного члена l_n . В оптически неоднородной среде (с плавно меняющимся n; траектория луча в такой среде — кривая линия), О. д. п. есть , где dl — бесконечно малый элемент траектории луча. Понятие О. д. п. играет большую роль в оптике, особенно в геометрической оптике и кристаллооптике, позволяя сопоставлять пути, проходимые светом в средах, в которых скорость его распространения различна. Геометрическое место точек, для которых О. д. п., отсчитываемая от одного источника, одинакова, называется поверхностью световой волны; световые колебания на этой поверхности находятся в одинаковой фазе.

Разность хода

лучей, разность оптических длин путей двух световых лучей, имеющих общие начальную и конечную точки. Понятие Р. х. играет основную роль в описании интерференции света и дифракции света. Расчёты распределения световой энергии в оптических системах основаны на вычислении Р. х. проходящих через них лучей (или пучков лучей).

Интерференция света,

сложение световых волн, при котором обычно наблюдается характерное пространственное распределение интенсивности света (интерференционная картина) в виде чередующихся светлых и тёмных полос вследствие нарушения принципа сложения интенсивностей

4) метод деления волнового фронта

В методе деления волнового фронта пучок, проходя через отверстия, делится на несколько пучков.

Свет, испускаемый обычными(не лазерными) источниками, не бывает строго монохроматическим.Поэтому для наблюдения интерференции свет от одного источника нужно разделить на два пучка и затем наложить их друг на друга. Существующие экспериментальные методы получения когерентных пучков из одного светового пучка можно разделить на два класса. В методе деления волнового фронта пучок пропускается, например, через два близко расположенных отверстия в непрозрачном экране.

Схема Юнга

Схема Юнга. Т. Юнг в 1807 г. впервые в своей публичной лекции продемонстрировал схему наблю­дение интерференции. Свет от источника S направлялся на узкую диафрагму S'. Дифрагировавший на диафрагме 5" свет попадал на экран с двумя узкими отверстиями Sj и S₂, расположенными на рас­стоянии / друг от друга (рис. 3.6). Если ширина щели ^'достаточно мала (см. § ), то волны, образо­ванные отверстиями Si и S₂, являются когерентными. На экране Э, расположенном на достаточно большом расстоянии D от S, и S₂, наблюдают интерференционную картину, представляющую чере­дующие темные и светлые участки. Интерференционная картина будет еще более четкой, если отвер­стия заменить щелями, параллельными Sи экрану. Интерференционная картина в этом случае будет иметь вид темных и светлых полос. Распределение интенсивности и ширина полос интерференции будут описываться соотношениями 3.20 и 3.23. Учет дифракции на ели S а также S_; и S₂ приводит к более сложным выражениям.

Бизеркала Френеля. Френель предложил в качестве когерентных источников использовать два мнимых изображения одного и того же источника. Рассмотрим вначале случай, когда мнимые источники создаются двумя зеркалами. Эта схема известна под названием бизеркал Френеля (рис. 3.7). Два плоских зеркала АО и ВО расположены под углом, близким к 180°, так, что угол а не превышает 1°. Для того, что­бы исключить попадание света от источника непосредственно на экран используется небольшой экран F. Нетрудно показать на основе закона отражения, что источник S и два его мнимых изображения 5; и S₂ будут находиться на окружности с центром в точке О, расположенной на линии пересечения зеркал АО и ВО. Кроме того, ZS_xORK = ZS₂OK = a. Рассматривая 5*_; и S₂ как когерентные точечные источники, мы можем использовать выражения (3.23) и (3.24) для описания распределения интенсивности интерферен­ции и ширины ее полос. В данном случае

D = acosa + b»a + b,

/ = 2а sin а

?

M

0

s%

N

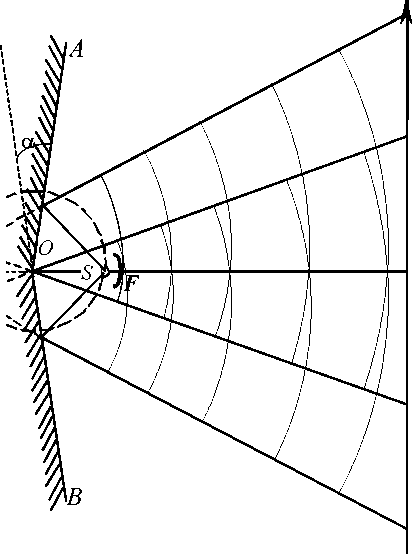
Рис. 3.7. Бизеркало Френеля

где a=SO, b=OK.

Подставляя (3.26) и (3.27) в (3.23) и (3.24), получим выражение для ширины полос

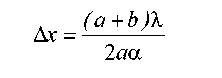
(3.27)

и распределения интенсивности на экране вдоль некоторого направления X

(3.28)

Из соотношения (3.27) и (3.28) следует, что интерференционная картина будет хорошо наблюдае-мой, если а->0и а<<Ъ. Количество наблюдаемых полос будет зависеть от ширины области перекрытия интерферирую 1их волн MN, а также от ширины каждой полосы. Если источник S является протяженным, то количество наблюдаемых интерференционных полос будет зависеть также от размеров источника

Бипризма Френеля. Бипризма представляет собой двойную призму с углом при вершине, близким к 180°. Преломляющий угол при этом является малым и, как правило, не превышает 30'. В этой схеме ис-точником света обычно служит ярко освещенная щель, установленная строго параллельно ребру призмы.

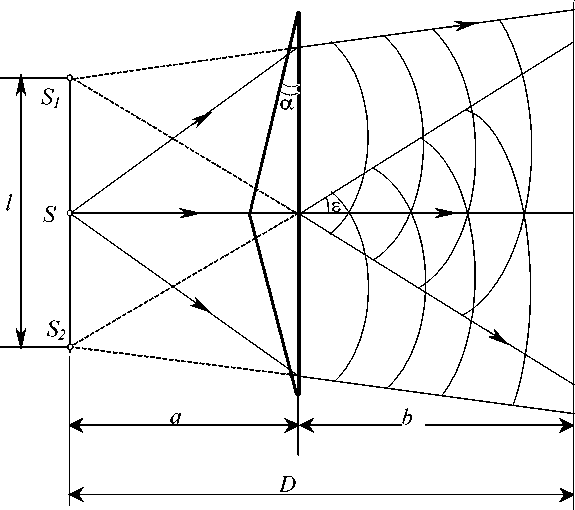
Рис. 3.8. Схема осуществления интерференции с помощью би-призмы Френеля.

Оптическая схема осуществления интерференции с помощью бипризмы Френеля приведена на рис.3.8.

Поскольку каждая половинка отклоняет лучи на небольшой угол S, приблизительно равный (и-1)х , то можно считать, что здесь образуется два мнимых источника S1 nS₂

Из рисунка 3.8 следует, что 2 1 (п - )а . Величина D = a + b. Поэтому ширина интер­ференционных полос

Аналогично предыду дему случаю, мы можем записать выражение для распределения интенсивности вдоль выбранного направлениях:

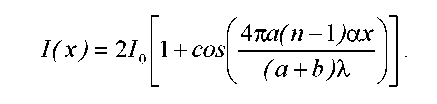
Если между источником S и бипризмой поместить собирающую линзу так, чтобы источник нахо­дился в её фокусе, то после преломления в призме будем иметь случай сложение плоских когерентных волн; интерференционная картина в этом случае будет описываться выражениями 3.10—3.13.

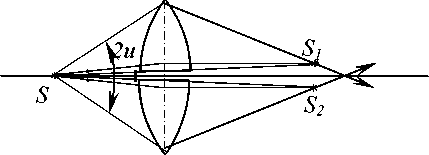
Билинза Бийе. В схеме, предложенной Бийе, собирающую линзу разрезают по диаметру и обе ее поло­винки раздвигают на небольшое расстояние, обычно не превышающее 1 мм. Если поместить точечный источник света или освещенную щель параллельно плоскости разреза на расстояние, больше фокусного, то после прохождения через обе половинки, свет будет образовывать два действительные изображения S₁ и 5*2 (рис. 3.9). В области перекрытия волн, идущих от S1 и S₂ будет наблюдаться интерференционная кар­тина¹. Полученные изображения будут являться когерентными источниками, поэтому мы можем приме-нить соотношения (3.23) и (3.24) для определения основных характеристик полученной интерференцион-

Рис. 3.9. Интерференционная схема с билинзой Бийе 1 Если источник S расположен между фокусами и линзой, то будут образовываться мнимые изображения. В этом слу-

чае перекрытия волн не будет.

ной картины: ширины полос и распределения интенсивности вдоль некоторого направления.

Схема Бийе позволяет рассмотреть некоторые общие закономерности, характерные для всех рас­смотренных схем. Угол 2м, образованный крайними лучами, исходящими из источника, называется апер­турой сходящихся пучков. Этот угол определяет область перекрытия интерферирующих волн. Угол 2ю, образованный лучами, идущими от источника к центральной точке экрана, соответствующей нулевой раз­ности хода, называется апертурой интерференции. Как будет показана в дальнейшем, апертура интерфе­ренции определяет максимальный размер источника (ширину щели), при котором интерференционная картина будет наблюдаться отчетливо.

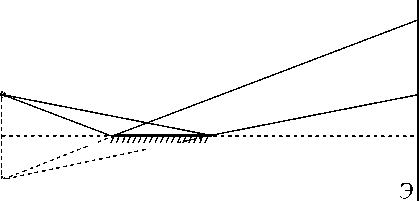Зеркало Ллойда. Свет от источника S падает под небольшим углом на отражающую поверхность. Ин­терференция на экране Э возникает при наложении волн от источника и его мнимого изображения Si (рис.3.10). Область перекрытия волн определяется длиной отрезкаMN.

N

М

Рис. 3.10. Интерференционная схема Ллойда

При отражении от зеркала происходит скачок фазы, равный пи, поэтому вся интерференционная кар­тина

оказывается сдвинутой на половину интерференционной полосы по сравнению со схемой Юнга.

5) полосы равной толщины

Полосы равной толщины и полосы равного наклона.

Полосы равной толщины и равного наклона наблюдаются при интерференции волн, отраженных от двух границ прозрачной пленки или плоскопараллельной пластинки.

Полосы равного наклона локализованы на бесконечности.

Полосы равной толщины локализованы в плоскости отражающей пленки. В пределах ширины пленки можно считать, что интерференционная картина локализована там, где вам удобнее.

Для наблюдения полос равной толщины отражающие поверхности не обязательно должны быть идеально плоскопараллельны. Пара отражающих плоскостей может образовывать тонкий клин. Могут быть соприкасающиеся поверхности, одна или обе из которых — сферические (кольца Ньютона).

Б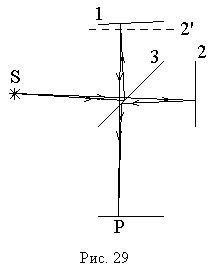олее того, две отражающих поверхности могут быть расположены в разных местах, как в интерферометре Майкельсона (рис. 29). Здесь — источник света, — экран для наблюдения интерференции отраженных волн от зеркал и , — полупрозрачная пластинка.

Если зеркало мысленно отразить в полупрозрачной пластинке , то его изображение примет положение . Вместе с зеркалом мысленно отобразим в полупрозрачной пластинке и все лучи, идущие справа от нее к зеркалу и от него обратно к полупрозрачной пластинке. Тогда на экран свет будет приходить, как бы отражаясь от двух плоскостей и . Если дополнить интерферометр двумя линзами, как это обычно делается (рис. 30), то, в зависимости от расстояния между линзой и экраном , можно наблюдать полосы равной толщины () или полосы равного наклона ().

6) зоны Френеля

Одной из самых простых дифракционных задач является дифракция на круглых отверстиях или круглых дисках (шариках). Если точечный источник света и точка наблюдения находятся на оси системы, то задача просто решается методом зон Френеля. Радиусы кольцевых зон Френеля в плоскости препятствия в случае падения плоского волнового фронта определяются выражением

где L – расстояние от препятствия до плоскости наблюдения, λ – длина волны света. Расчеты показывают, что амплитуды колебаний вторичных волн в точке наблюдения от каждой зоны одинаковы, но колебания, возбуждаемые соседними зонами, отличаются по фазе на π. Поэтому при увеличении радиуса круглого отверстия интенсивность света в центре дифракционной картины будет обращаться в ноль, если на отверстии укладывается четное число зон, и достигать максимума при нечетном числе зон.

Если перекрыть непрозрачным экраном зоны Френеля через одну, то можно получить значительное усиление интенсивности колебаний в точке наблюдения, так как колебания только от четных (или только от нечетных) зон происходят в одной фазе. Такие устройства называют зонными пластинками Френеля. Они действуют подобно линзе.

При дифракции света на круглом диске в центре дифракционной картины всегда наблюдается светлое пятно (пятно Пуассона).

Общий вид дифракционной картины при дифракции света на круглых препятствиях достаточно сложен.

Для каждого положения точки наблюдения в стороне от оси симметрии результирующее колебание может быть найдено путем сложения колебаний от всех вторичных источников с учетом фазовых соотношений. Метод зон Френеля неприменим при нарушении осевой симметрии задачи. Определение результатов интерференции вторичных волн, в общем является сложной математической задачей, которая может быть решена с помощью компьютерного моделирования.

В данной компьютерной модели в нижнем левом окне изображены границы зон Френеля, определенные для точки наблюдения, находящейся на оси симметрии. Программа позволяет оставлять открытыми или закрывать непрозрачным экраном целые зоны Френеля. Для каждого случая компьютер рассчитывает дифракционную картину во всей плоскости наблюдения. Таким путем могут быть получены дифракционные картины при дифракции на зонных пластинках и продемонстрировано их фокусирующее действие.

Модель позволяет изменять длину волны λ. На экране дисплея высвечивается отношение интенсивностей I / I₀ в центре дифракционной картины, где I₀ – интенсивность колебаний в точке наблюдения в отсутствие препятствия.

Обратите внимание, что если открыть только две соседние зоны, то в центре дифракционной картины возникает темное пятно. Если открыта только одна любая зона, то интенсивность колебаний в центре дифракционной картины в 4 раза превосходит I₀.

Спираль Френеля

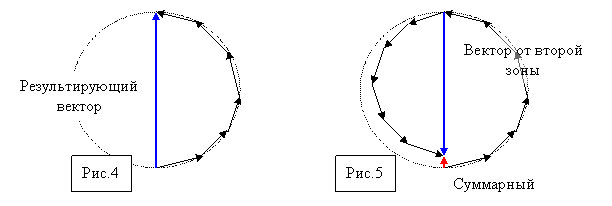
         Совершенно очевидно, что, то что мы приписываем каждой зоне Френеля одну и туже фазу есть лишь приближение, так как фаза будет плавно меняться от границы начала зоны до её конца. Однако с каждой зоной можно поступить как со всей волновой поверхностью. Разобьем каждую зону Френеля на кольцевые зоны, аналогичные зонам Френеля, но гораздо меньшие по ширине. Будем складывать колебания от этих узких зон графическим методом. Амплитуду от каждой зоны будем изображать вектором, модуль которого медленно убывает при  переходе от зоны к зоне. Каждое следующее колебание отстает по фазе на одну и туже величину. Векторная диаграмма от первой зоны Френеля будет иметь вид как на рис.4.

Результирующий вектор совпадает с диагональю окружности, на которой расположились вектора – амплитуды от узких зон. Из-за монотонного убывания амплитуд векторы образуют не замкнутую фигуру, а ломанную спиралевидную линию. Результирующий вектор от второй зоны Френеля направлен противоположно вектору первой зоны, но немного меньше его по модулю, поэтому их сумма не будет точным нулем, а даст небольшой суммарный вектор в нижней части рис.5.

Результирующий вектор

Рис.4

Рис.5

Суммарный

Вектор от второй зоны

 Сумма амплитуд от всех зон Френеля (от всей волновой поверхности) изображена на рис.6. Видно, что амплитуда равна половине амплитуды от первой зоны Френеля. На рс.7 изображен вектор, отвечающий внутренней половине первой зоны Френеля. Он в больше вектора всей волновой поверхности.

 

Рис.6

Суммарный

Вектор от ½ первой зоны Френеля

Рис.7

Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно, взаимно ослабляют друг друга. Если поставить на пути волны пластинку, которая перекрывала бы все четные или все нечетные зоны, то интенсивность света в точке Р резко возрастает. Такая пластинка называется амплитудной зонной пластинкой. Ещё большего эффекта можно добиться, не перекрывая зоны, а изменяя их фазу на π.  Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, соответствующих четным и нечетным зонам, отличается по толщине на соответствующим образом подобранную величину. Впервые это было осуществлено Робертом Вудом, с помощью травления тонкого слоя прозрачного лака. Такая пластинка называется фазовой зонной пластинкой. По сравнению в амплитудной зонной пластинкой фазовая  дает дополнительное увеличение амплитуды в два раза, а интенсивности света в четыре раза.

         Усиление интенсивности света зонной пластинкой эквивалентно фокусирующему действию линзы. Расстояния от зонной пластинки до источника и его «изображения» связаны таким же соотношением, как и для линз. Что бы убедится в этом, перепишем формулу (7) следующим образом:

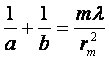          .                                                                                (10)

Выражение в правой части можно рассматривать как фокусное расстояние

         ,

но в отличии от линзы, зонная пластинка – система не таутохронная: колебания, приходящие в фокус от соседних открытых зон, различаются по фазе на π. Кроме основного фокуса, зонная пластинка имеет и другие, а именно те точки, в которые колебания приходят от соседних открытых зон с разностью хода 2λ, 3λ и т. д. Эти фокусы оказываются более слабыми по сравнению с основным.

7) дифракция на щели

льшое практическое значение имеет случай Дифракция света на щели. При освещении щели параллельным пучком монохроматического света на экране получается ряд тёмных и светлых полос, быстро убывающих по интенсивности. Если свет падает перпендикулярно к плоскости щели, то полосы расположены симметрично относительно центральной полосы (рис. 2), а освещённость меняется вдоль экрана периодически с изменением j, обращаясь в нуль при углах j, для которых sin j = m/lb (m = 1, 2, 3 ....). При промежуточных значениях освещённость достигает максимальных значений. Главный максимум имеет место при m = 0, при этом sin j = 0, т. е. j = 0. Следующие максимумы, значительно уступающие по величине главному, соответствуют значениям j, определённым из условий: sin j = 1,43 l/b, 2,46 l/b, 3,47 l/b и т.д.   С уменьшением ширины щели центральная светлая полоса расширяется, а при данной ширине щели положение минимумов и максимумов зависит от l, т. е. расстояние между полосами тем больше, чем больше l. Поэтому в случае белого света имеет место совокупность соответствующих картин для разных цветов. При этом главный максимум будет общим для всех l и представится в виде белой полоски, переходящей в цветные полосы с чередованием цветов от фиолетового к красному.