Частные коэффициенты корреляции

Частные коэффициенты корреляции определяют силу линейной зависимости между двумя переменными без учета влияния на них других переменных. При изучении многомерных связей парные коэффициенты корреляции могут давать совершенно не верные представления о характере связи между двумя переменными. Например, между двумя переменными X и Y может быть высокий положительный коэффициент корреляции не потому, что одна из них стимулирует изменение другой, а оттого, что оби эти переменные изменяются в одном направлении под влиянием других переменных, как учтенных в модели, так и возможно, неучтенных. Поэтому необходимо измерять действительную силу линейной связи между двумя переменными, очищенную от влияния на рассматриваемую пару переменных других факторов, т.е. необходимо рассчитать частные коэффициенты корреляции.

В общем случае выборочный частный коэффициент корреляции между переменными x_i и x_j обозначается ,

Если необходимо учесть и влияние y: ;

Пусть эмпирические парные коэффициенты корреляции между всевозможными парами представлены в виде корреляционной матрицы:

,

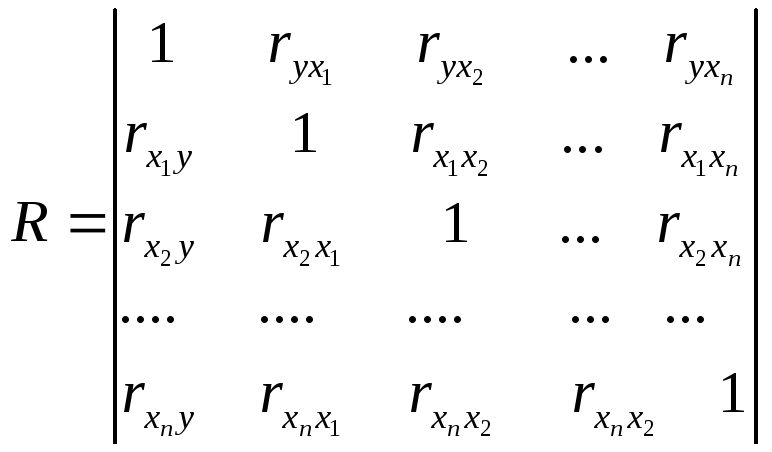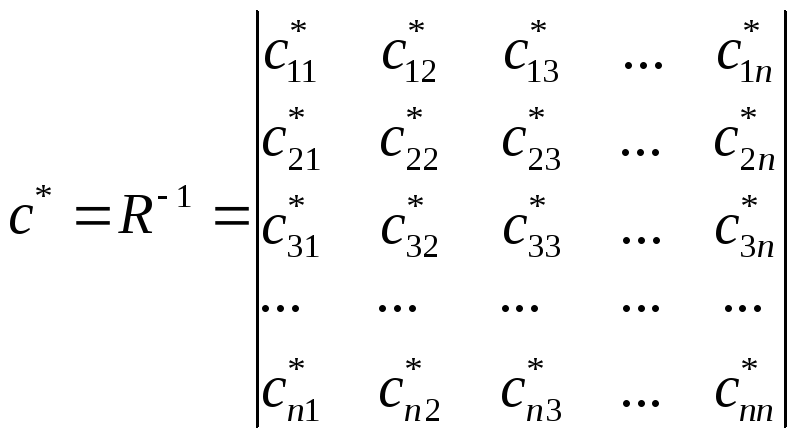, где - обратная матрица к матрице R, тогда (1)

Из общей формулы (1) можно получить частные формулы для трех переменных и для четырех переменных ; .

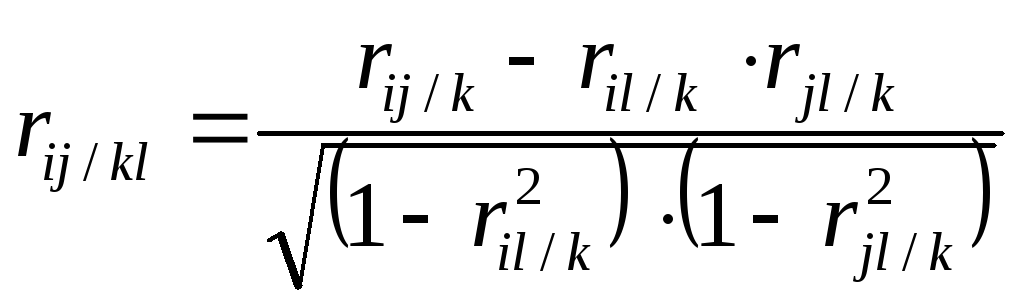Значимость коэффициентов корреляции как частных, так и общих производится с помощью t-критерия Стьюдента. Отбираются факторы , для которых частные коэффициенты корреляции незначимы.

Множественная регрессионная модель строится так, сначала рассчитываются общие коэффициенты корреляции и , проверяется их значимость. Затем рассчитывают частные коэффициенты корреляции и , проверяется их значимость. В модель включают факторы , для которых связь с y значима, а между и связь незначима, т.е. частные коэффициенты должны быть значимыми, а - незначимыми.

Множественная линейная регрессия

Множественная линейная регрессия является простейшим формой множественной зависимости. Ее уравнение записывается в виде (1)

где - результирующий показатель (зависимая переменная); - независимый фактор.

Запишем уравнения (1) в матричной форме.

Пусть Х – матрица N наблюдений по n факторам (),

Y - матрица – столбец наблюдений по результирующему показателю (1 х N),

A - матрица-столбец неизвестных параметров уравнения регрессии ():

,

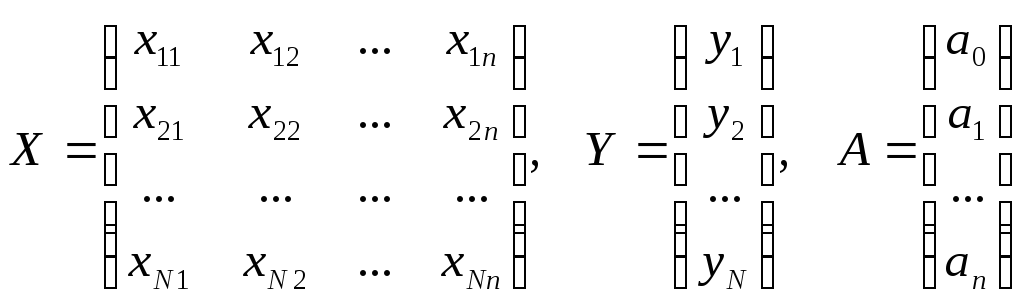где x_ij – i –ое () наблюдение по j –ому () фактору.

Ввиду того, что размерность матрицы-столбца А есть , матрицу Х дополним слева столбцом из единиц и обозначим :

.

Тогда уравнение (1) можно записать в матричном виде: (2). Транспонируем матрицу (строки и столбцы поменяем местами, превращаем в ): , где - матрица, транспонированная к матрице .

Умножим левую и правую части уравнения (2) слева на матрицу : (3).

Уравнение (3) является системой нормальных уравнений, полученной на основании уравнения регрессии (1) и записанной в матричной форме.

Пусть – матрица, обратная матрице . Тогда, умножив слева на эту матрицу левую и правую части уравнения (3), получим . Откуда следует, что коэффициенты уравнения регрессии (1) могут быть определены по формуле:

,

где – элементы обратной матрицы .

Для уравнения с двумя объясняющими переменными (n=2):