Корреляционное отношение  всегда положительно 0   1.

Чем теснее связь между y и х, тем меньше величина , , тем больше .

Точность аппроксимации определяется как средняя относительная ошибка аппроксимации .

Величина  определяется в процентах. Чаще применяется при оценке нелинейной зависимости. Если  менее 3-5%, то точность высокая, если 5-10% - умеренная, 10% и более – низкая.

Оценка значимости коэффициента корреляции и коэффициентов уравнений регрессии. Оценка значимости коэффициента корреляции

Поскольку коэффициент корреляции r определяется по данным случайной выборки, то он может отличаться от коэффициента корреляции , который соответствует генеральной совокупности.

В случае, когда объем выборки N  20, то предполагают, что коэффициент корреляции является случайной величиной, распределенной по нормальному закону.

Пусть _r – среднеквадратичное отклонение выборочного коэффициента корреляции r. Тогда при N  20 доверительный интервал для r будет равен ( - x_p_r,  + x_p_r), где х_р – параметр нормального распределения вероятностей:

.

Значение х_р определяется по таблице функции распределения Ф(х) в зависимости от вероятности Р. Для оперативного определения значения х_р при Р  0,9, можно использовать таблицу 2.

Таблица 2.

Ф(хp)	0,9	0,95	0,99
хр	1,653	1,96	2,576

Значение среднеквадратичного отклонения _r можно определить по формуле .

Подставим в доверительный интервал вместо неизвестной величины  его оценку по выборке r и _r . Тогда

. Для проверки значимости выборочного коэффициента корреляции r чаще используется так называемая нулевая гипотеза: H₀:  = 0 (H₁:   0).

Суть нулевой гипотезы состоит в том, что в случае, когда для случайных величин х и y на основании выборок и полученоr>0, т.е. между ними имеется корреляционная связь, предполагается, что в генеральной совокупности этой связи нет (H₀:  = 0).

При  = 0, получим:

.

При проверке нулевой гипотезы достаточно использовать только левый (нижний) предел доверительного интервала . Так как  = 0, то .

Данное условие означает, что нулевая гипотеза с вероятностью Ф(х_р) подтверждается.

Если , то нулевая гипотеза с вероятностью Ф(х_р) отвергается, а, следовательно, связь между х и y имеет место.

В тех случаях, когда размер выборки N<30, для проверки нулевой гипотезы ( = 0) используется t – критерий Стьюдента.

Алгоритм использования t – критерия Стьюдента

1. а) Для анализа значимости коэффициента корреляции 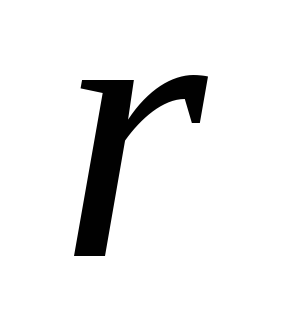определяется расчетное значение 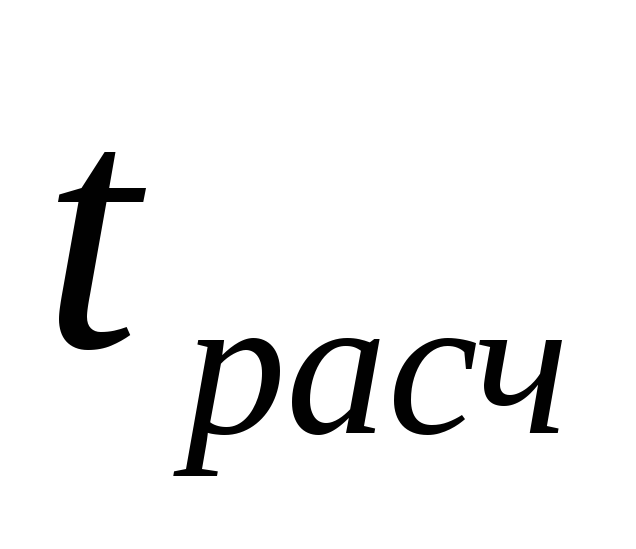по формуле 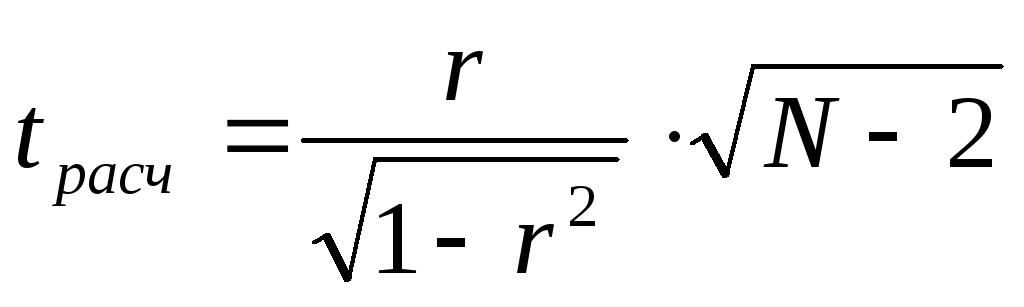(если N<30)

(если N>30)

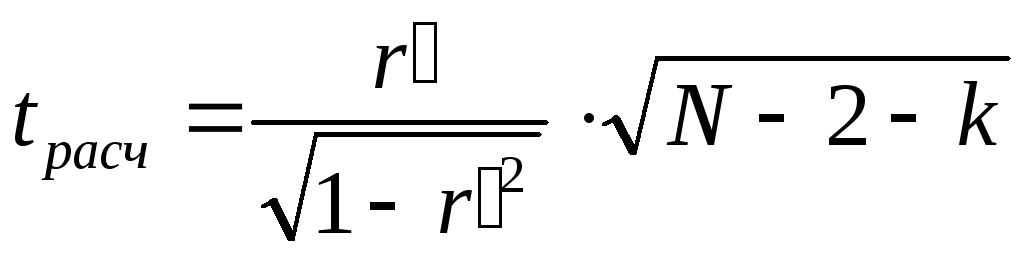б) Для анализа значимости частного коэффициента корреляции определяется расчетное значение t_расч. по формуле: , где - частный коэффициент корреляции, k – номер частного коэффициента корреляции (k – число исключенных факторов).

в) Для анализа значимости корреляционного отношения определяется расчетное значение t_расч. по формуле:

2. По таблице критических точек распределения Стьюдента по значению числа степеней свободы k = N - n (n – число параметров) и уровню значимости  (уровень значимости - это вероятность совершить ошибку первого рода, т.е. отвергнуть правильную нулевую гипотезу) определяется теоретическое значение t_теор. (критическая точка).

Таблица 3.

Таблица критических точек для =5%

k	1	3	5	10	15	20	30	40	50	75	100	150	200
t	12,7	3,18	2,57	2,23	2,13	2,09	2,04	2,02	2,01	1,99	1,98	1,98	1,97

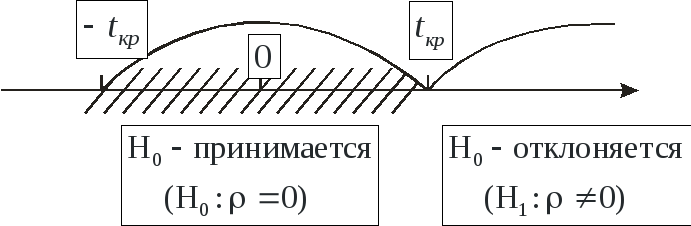
Рис.1.

Если t_расч  t_теор., то нулевая гипотеза Н₀ принимается ( = 0), если t_расч > t_теор., то Н₀ – отвергается (  0), следовательно, случайные величины х и y коррелированы, то есть между ними существует линейная связь, следовательно:

1. коэффициент корреляции r значим;

2. частный коэффициент корреляции 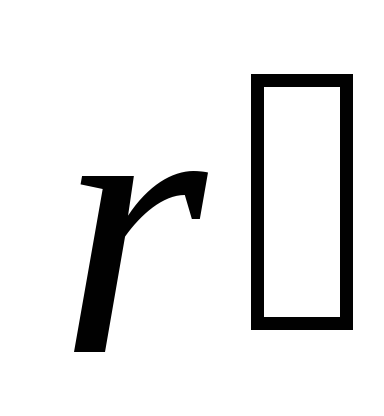значим;

3. корреляционное отношение 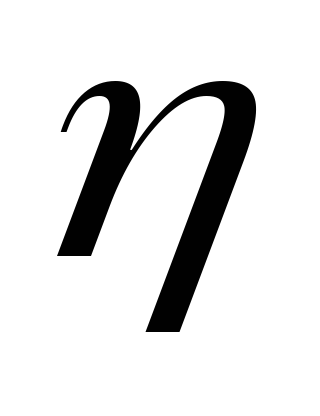значимо.

Оценка значимости коэффициентов уравнений регрессии

В общем случае значимость коэффициентов уравнений регрессии определяется с помощью t – критерия Стьюдента.

Линейная зависимость: .

Для коэффициентов уравнения регрессии а_к (k = 1,2):

,

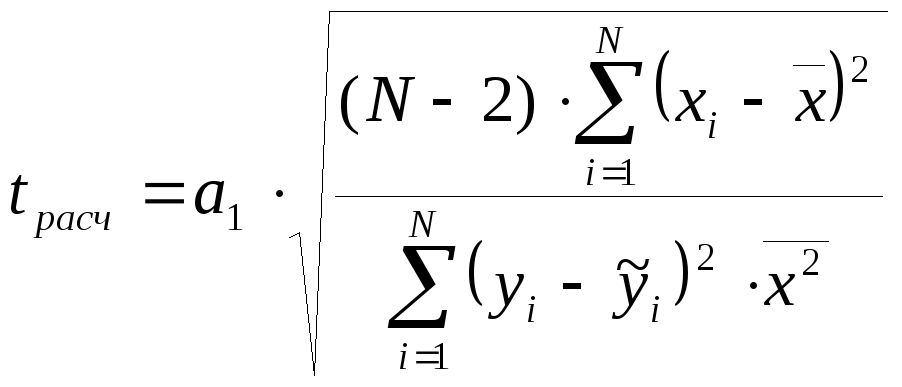Теоретическое значение t – критерия Стьюдента t_теор находится аналогично коэффициенту корреляции r.

По той же схеме проверяется нулевая гипотеза: H₀ : a_k = 0 (H₁ : a_k  0). Гипотеза в такой постановке называется гипотезой о статистической значимости коэффициента регрессии. Если гипотеза Н₀ принимается, то полагают, что у не зависит от х, а коэффициент a_k считается статистически незначимым. При отклонении гипотезы Н₀ коэффициент a_k считается статистически значимым, что указывает на наличие определенной линейной зависимости между y и х. В данном случае рассматривают двустороннюю критическую область, так как коэффициент регрессии может быть как положительным, так и отрицательным (а_к > 0 или а_к < 0).

Если t_расч  t_теор., то Н₀ принимается и а_к = 0, если t_расч > t_теор, то Н₀ отвергается и а_к  0.

Для парной регрессии более важным является анализ статистической значимости коэффициента а₂ , так как именно в нем скрыто влияние независимой переменной х на зависимую y.

При оценке значимости коэффициента линейной регрессии на начальном этапе можно использовать «грубое» правило, позволяющее не прибегать к таблицам:

1. Если t_расч  1, то а_к = 0, т.е. коэффициент а_к незначим, так как доверительная вероятность при двусторонней альтернативной гипотезе составит менее, чем 0,7.

2. Если 1<t_расч  2, то а_к относительно (слабо) значим, доверительная вероятность лежит между значениями 0,7 и 0,95.

3. Если 2<t_расч.  3, то коэффициент а_к значим и связь между х и у имеет линейный характер. В этом случае доверительная вероятность колеблется от 0,95 до 0,99.

4. Если t_расч > 3, то это почти гарантия наличия линейной связи.

Для N > 10 предложенное «грубое» правило практически всегда работает.

Степенная зависимость: .

Линеаризуя данную зависимость, получим

lnỹ = lna₁ + а₂  lnx или , где , .

Для полученного линейного уравнения имеем:

,

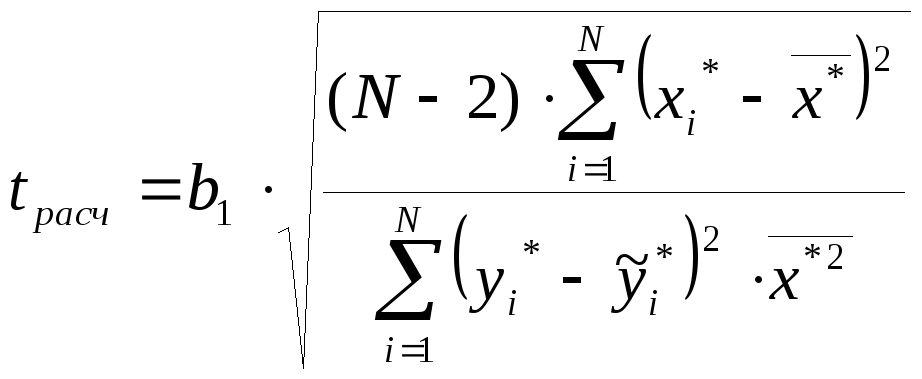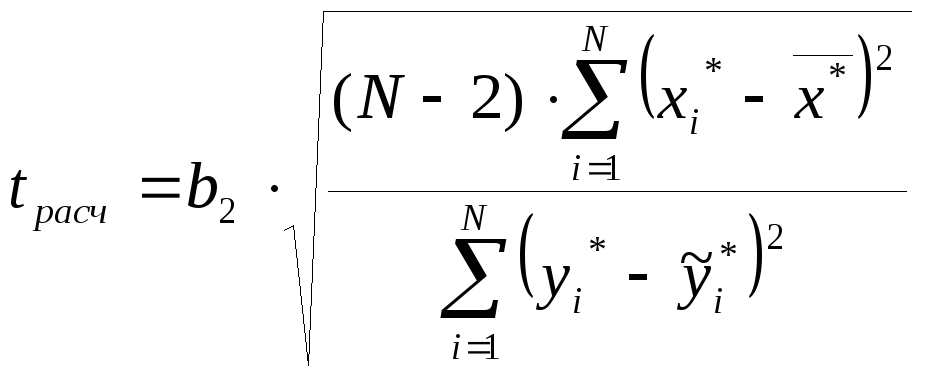
где b₁ = a₁^*, b₂ = a₂.

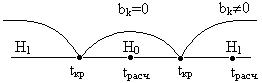
Рис.2.

Значение t_теор. находится аналогично линейной зависимости (Рис.2.).

Если t_расч  t_теор., то b_к = 0, коэффициент b_к незначим.

Если t_расч > t_теор, то b_к  0, коэффициент b_к значим.

Если b₁ = a₁^*= lna₁ = 0, то а₁ = 1 и ,

Если b₂ = a₂ = 0, то .

Гиперболическая зависимость:

Значимость коэффициентов по нулевой гипотезе определяется так же, как и при линейной зависимости, с одной разницей: при вычислении t_расч в формуле вместо x_i и берутся:

и .

Логарифмическая зависимость: .

Значимость а₁ и а₂ определяется по той же схеме. Вместо х_i и берутся и .

Параболическая зависимость:

Для проверки значимости коэффициента а_к (k = 1,2..n), значение t_расч определяется по формуле:

,

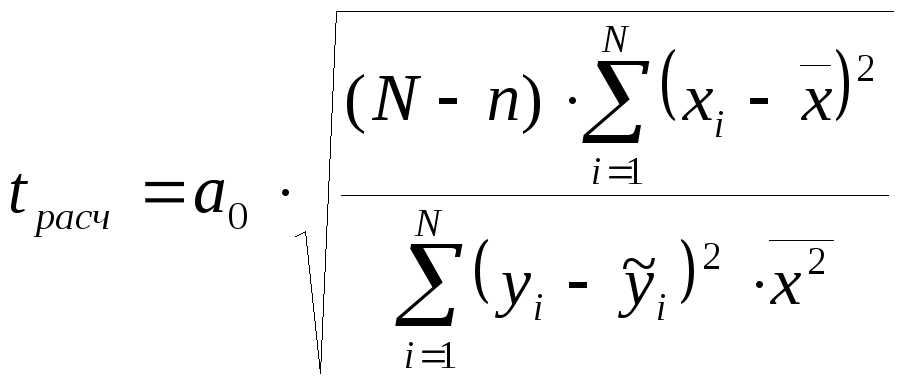
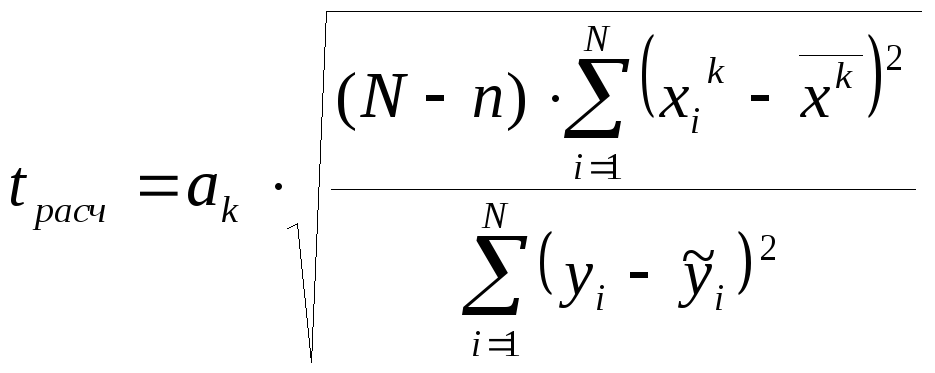где n – число коэффициентов регрессии.

При определении значимости коэффициента а₀ в формуле t_расч показатели степени к при х_i и берутся равными единице (k= 1).

Тригонометрическая зависимость:

представляется в виде линейной зависимости: ,

где , .

Значимость коэффициента а_к,() оценивают по формуле:

.

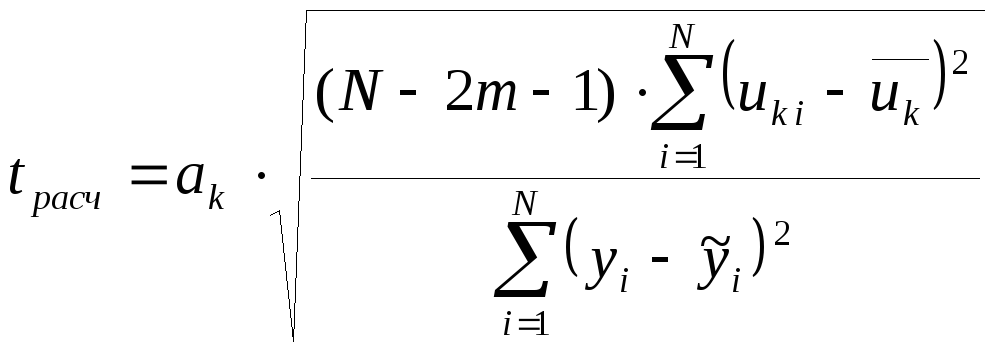Значимость коэффициента b_к () определяют по формуле:

.

Значимость коэффициента а₀ () рассчитывают по формуле: