
- •Регрессионный анализ
- •Основные виды уравнений парной регрессии и методы определения их параметров
- •Алгоритм применения мнк
- •Линейная зависимость
- •Гиперболическая зависимость
- •Степенная зависимость
- •Логарифмическая зависимость
- •Параболическая зависимость
- •Тригонометрическая зависимость
- •Корреляционное отношение всегда положительно 0 1.
- •Оценка значимости коэффициента корреляции и коэффициентов уравнений регрессии. Оценка значимости коэффициента корреляции
- •Оценка значимости коэффициента детерминации (значимость уравнения регрессии в целом)
- •Автокорреляция остатков. Критерий Дарбина – Уотсона
- •Выбор формы уравнения регрессии
- •Множественная регрессия
- •Частные коэффициенты корреляции
- •Множественная линейная регрессия
- •Оценка параметров уравнения линейной регрессии
- •Множественная нелинейная регрессия. Алгоритм метода Брандона
- •Спецификация множественной регрессии
- •Приложение 2. Распределение Дарбина—Уотсона
Выбор формы уравнения регрессии
Форма уравнения регрессии выбирается из числа рассмотренных регрессионных зависимостей, для этого выполняют следующие операции:
1) Для каждой зависимости определяют:
-
Неизвестные параметры (ak, bk,
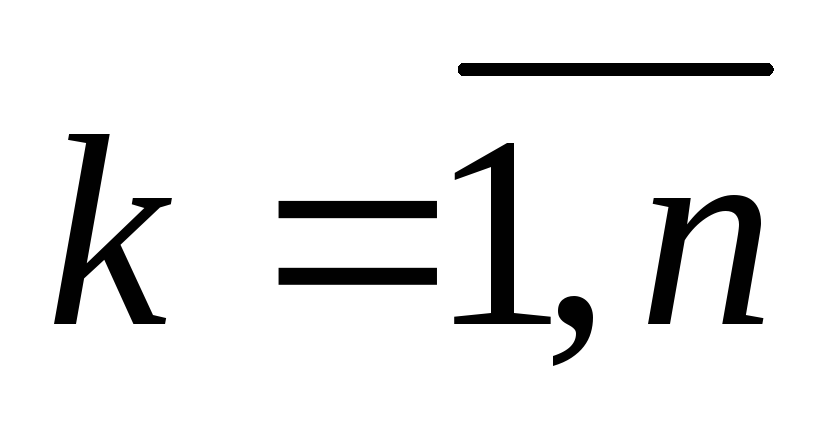 )
и их значимость;
)
и их значимость; -
Корреляционное отношение (для линейной зависимости коэффициент корреляции r) и значимость
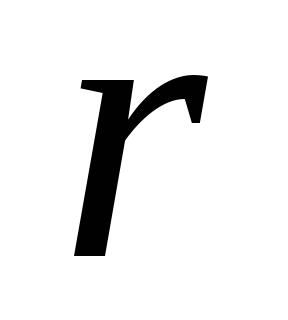 или
или
 ;
; -
Значимость уравнения в целом;
-
Критерий автокорреляции DW;
-
Точность аппроксимации .
2)
Из зависимостей выбирают такие, у которых
автокорреляция остатков отсутствует,
т.е. d2
DW<
4-d2
,все
параметры значимы, значим
![]() или
или
![]() ,
уравнение в целом значимо.
,
уравнение в целом значимо.
3) Из числа выбранных зависимостей выбирается зависимость, имеющая наибольшее значение корреляционного отношения (r – для линейной зависимости). Если таких зависимостей несколько, то предпочтение отдается той, у которой коэффициент меньше, при этом линейной зависимости независимо от величин отдается предпочтение.
Множественная регрессия
В
множественной регрессии в отличие от
парной на зависимую случайную переменную
(результирующий показатель)
![]() воздействуют
одновременно n
(n>1)
независимых факторов x1,
x2,
.. , xn.
Уравнение множественной регрессии
записывается в виде:
воздействуют
одновременно n
(n>1)
независимых факторов x1,
x2,
.. , xn.
Уравнение множественной регрессии
записывается в виде:
![]() .
.
Коэффициент
корреляции зависимости между результирующим
показателем y
и каждым j
– м (![]() )
фактором xj
должен быть
отличен от нуля:
)
фактором xj
должен быть
отличен от нуля:
![]() .
.
При
проверке по нулевой гипотезе, которая
утверждает, что в генеральной совокупности
связи между y
и xj
нет
![]() ,
хотя по выборке
,
хотя по выборке
![]() корреляционная связь имеется, нулевая
гипотеза не должна подтверждаться при
P
= 0,9.
корреляционная связь имеется, нулевая
гипотеза не должна подтверждаться при
P
= 0,9.
Факторы
x1,
x2,
.. , xn
должны быть
попарно независимыми:
![]() .
При проверке значимости коэффициентов
корреляции зависимости между xk
и xj
.
При проверке значимости коэффициентов
корреляции зависимости между xk
и xj
![]() по нулевой гипотезе, она должна
подтверждаться (
по нулевой гипотезе, она должна
подтверждаться (![]() )
при P = 0,9.
)
при P = 0,9.
В отличие от парной регрессии в множественной отдельно рассматриваются только два вида зависимостей: линейная и нелинейная.
Они отличаются только алгоритмами построения уравнений регрессии. Общим для них является способ выбора из заданного множества факторов, попарно независимых.
Пусть на результирующий показатель y воздействуют факторы х1,х2 ,х3, х4 . Для каждой пары факторов определяются коэффициенты корреляции, которые примем равными: r1,2 = 0,85; r1,3 = 0,22; r1,4 = 0,64; r2,3 = 0,75; r2,4 = 0,08; r3,4 = 0,45.
В результате проверки значений rk,j по нулевой гипотезе получим 1,3 = 2,4 = 0, а остальные k,j 0.
Отсюда следует, что попарно независимыми являются следующие пары факторов: х1,х3 и х2, х4 .
Таким образом, в рассматриваемом случае в качестве независимых факторов могут быть взяты либо х1,х3 , либо х2, х4 . Какой группе факторов отдать предпочтение, зависит от величины совокупного воздействия каждой из них на результирующий показатель y. Берется та пара, у которой коэффициент корреляции совокупного воздействия R на y больше.
В
случае, когда число независимых факторов
равно n
![]() D
– определитель вида
D
– определитель вида
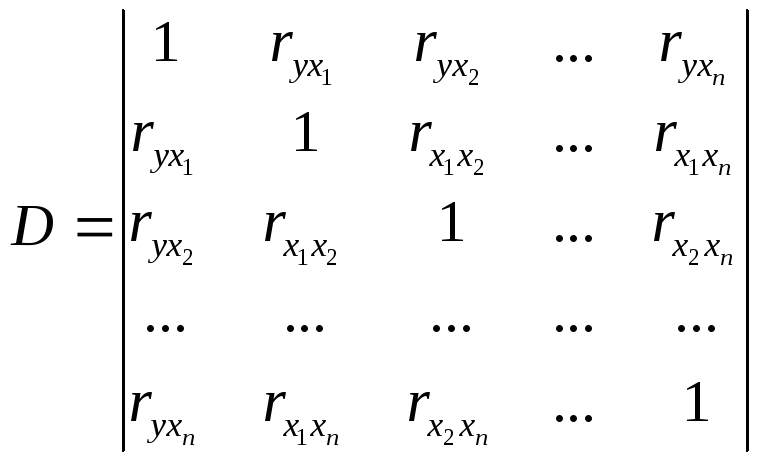 ,
,
![]() - определитель D
без первой строки и первого столбца:
- определитель D
без первой строки и первого столбца:
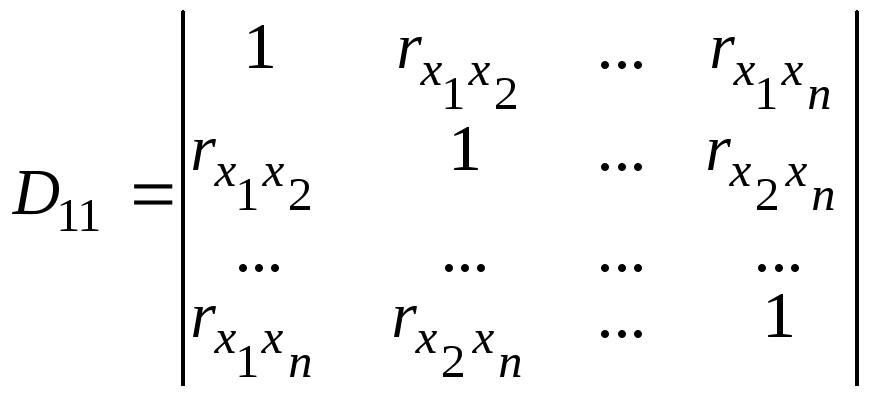 .
.
Предположим, что
в рассматриваемом примере
![]()
Тогда для пары x1 , x3 имеем

![]()
![]() .
.
Для
пары x2
, x4,
выполняя
аналогичные действия, находим
![]() .
.
Так как для пары x1, x3 Rx1x3 больше, чем для пары x2,x4 , то в качестве независимых факторов предпочтительнее взять x1 и x3.
