Регрессионный анализ

Регрессионный анализ – раздел математической статистики, главная задача которого состоит в выводе на основании соответствующих выборочных совокупностей уравнения регрессии, устанавливающего связь между значениями зависимой (эндогенной) переменной (результирующим показателем) и значениями независимых (экзогенных) переменных.

Указанную связь будем записывать в виде:, где - результирующий показатель; – j-й независимый параметр (фактор, воздействующий на результирующий показатель ()).

Совокупность методов, определяющих тесноту связи между y и x_j, составляет другой раздел математической статистики - корреляционный анализ. Если связь между переменными y и x является нефункциональной, установлена на основании совместного анализа соответствующих им выборок y₁, y₂, … , y_N и x₁, x₂, … , x_N, то считается, что между ними существует корреляционная связь.

Регрессия называется парной, если на y действует только один фактор (n = 1), и множественной, если число факторов, воздействующих на y, более одного (n > 1).

Уравнение линии регрессии (линии связи) при парной регрессии записывается в виде: ỹ= f (x).

Если при функциональной зависимости y=f(x) одному значению независимой переменной х соответствует только одно значение зависимой переменной y, то при корреляционной зависимости каждому значению х может соответствовать сколь угодно много значений y. Поэтому изменение х при корреляционной зависимости вызовет изменение не конкретного y, а среднего значения , и это изменение будет тем больше, чем теснее y и х будут корреляционно зависимы.

Тесноту связи определяют с помощью коэффициента корреляции r, который находится в пределах .

Если r = 0, то между случайными величинами y и х линейной связи нет (может иметь место параболическая, степенная, логарифмическая и т.п. связь, но не линейная ).

Если , то между величинами y и х существует функциональная связь: y = f (x).

При r > 0 имеет место прямая зависимость, т.е. с увеличением х увеличивается y, а при r < 0 – обратная зависимость - с увеличением х уменьшается y.

Если , то между случайными величинами y и х существует только корреляционная связь: .

Коэффициент корреляции находится по формуле:

, (1)

где

, , ,

Для вычисления r по значениям выборочных данных x_i и y_i, , формулу (1) преобразуем к виду (2):

(2)

Основные виды уравнений парной регрессии и методы определения их параметров

Выбор формулы связи (вида уравнения) называется спецификацией уравнения регрессии.

Перечислим основные виды уравнений парной регрессии:

• Линейная зависимость ;

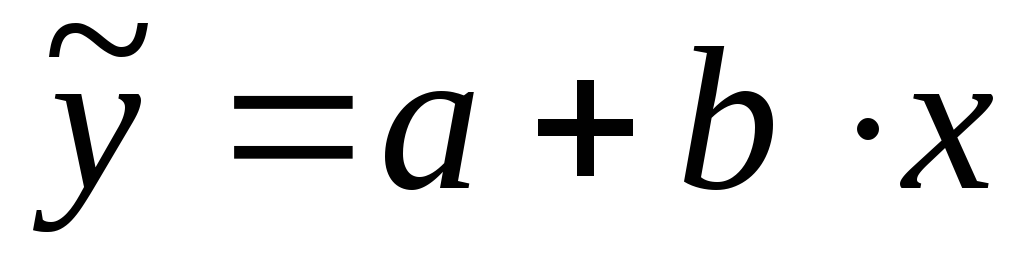• Гиперболическая зависимость ;

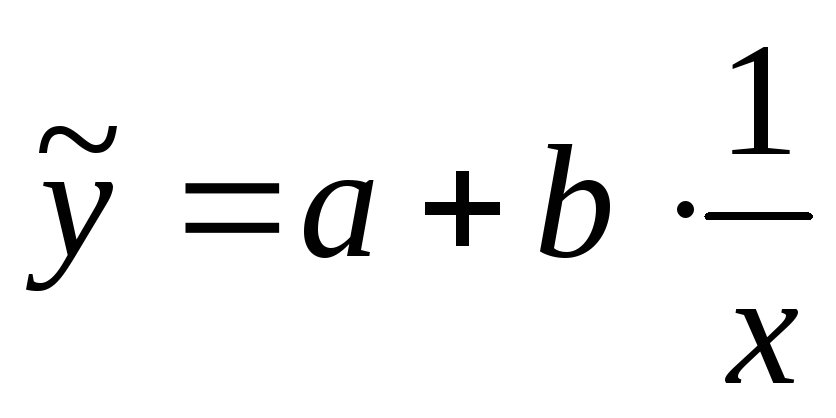• Степенная зависимость;

• Логарифмическая зависимость ;

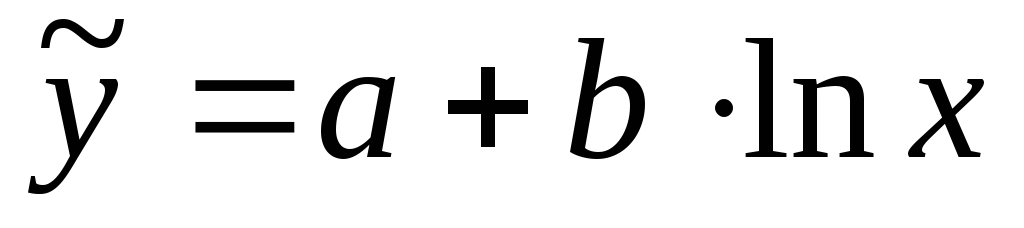• Полиномиальная зависимость ;

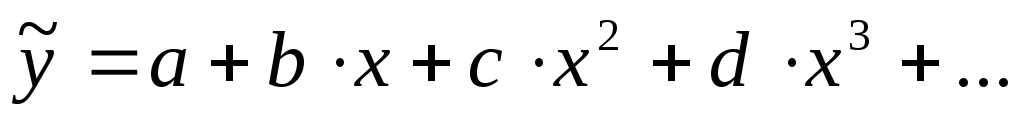• Тригонометрическая зависимость ; где m – число гармоник; a₀, a_k, b_k – неизвестные коэффициенты линии регрессии.

Определение параметров уравнения регрессии называется параметризацией.

Для определения неизвестных параметров уравнения регрессии обычно применяют метод наименьших квадратов (МНК). Рассмотрим функцию вида .

Алгоритм применения мнк

1. Строится целевая функция

2. Находится система уравнений для определения неизвестных параметров

Согласно МНК для нахождения параметров полинома p-ой степени необходимо решить систему так называемых нормальных уравнений:

Решение этой системы относительно и дает искомые значения параметров.