
- •1 Социальные информационные сети как объект защиты от деструктивных управляющих воздействий
- •1.1 Структурные и функциональные особенности социальных информационных сетей
- •1.1.1 Специфика понятие социальной информационной сети
- •1.1.2 Классификация социальных информационных сетей
- •1.1.3 Структура социальных информационных сетей
- •1.1.3 Свойства социальных информационных сетей
- •1.2 Моделирование процессов, протекающих в социальных информационных системах
- •1.2.1 Анализ социальных информационных сетей
- •1.2.2 Применение теории графов в моделировании сис
- •1.2.3 Модели влияния в сис
- •1.2.4 Сравнительная характеристика моделей
- •1.3 Угрозы, возникающие в социальных информационных системах
- •1.5 Основные выводы по главе
1.2.2 Применение теории графов в моделировании сис
В процессе эволюции
СИС может быть представлена как
ориентированный граф
 ,
где
,
где
 - некоторый профиль пользователя
(пользователь СИС), а любое ребро графа
- некоторый профиль пользователя
(пользователь СИС), а любое ребро графа
 имеет временную метку
имеет временную метку
 .
Отсюда,
.
Отсюда,
 отображает определенный момент времени,
когда была добавлена вершина
отображает определенный момент времени,
когда была добавлена вершина
 или ребро
или ребро
 в граф
в граф
 в некоторый момент времени
в некоторый момент времени
 существует граф
существует граф
 ,
который содержит все вершины и ребра,
добавленные к моменту времени
,
который содержит все вершины и ребра,
добавленные к моменту времени
 .
Такое представление СИС позволяет
отследить эволюционные процессы,
происходящие в ней.
.
Такое представление СИС позволяет
отследить эволюционные процессы,
происходящие в ней.
В графе СИС выделяют три типа пользователей:
-
пользователи, у которых больше всего прямых связей, чаще всего это лидеры СИС, имеющие большое влияние на других пользователей и являются активными распространителями информации;
-
субъекты, связывающие людей из различных подгрупп, которые между собой никак не пересекаются и быстрее всех других участников СИС распространяют информацию среди друзей;
-
субъекты, которые не хотят или не могут заводить больше связей, чем у них есть, поэтому распространение ими информации идет медленно и охватывает небольшие группы пользователей.
Большинство взаимных связей устанавливаются в относительно короткое время (в течение приблизительно одного дня). Отсюда, при описании СИС можно использовать неориентированный граф.
Рассмотрим
неориентированный граф, пусть
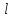 - путь между парой вершин графа (среднее
кратчайшей расстояние), тогда
- путь между парой вершин графа (среднее
кратчайшей расстояние), тогда
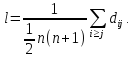
где
 - длина пути от точки
- длина пути от точки
 до точки
до точки
 .
.
Более точный способ
вычислить
 как среднее кратчайшее гармоническое
расстояние
как среднее кратчайшее гармоническое
расстояние
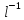 между парами вершин, в таком случае
будет справедливо выражение:
между парами вершин, в таком случае
будет справедливо выражение:
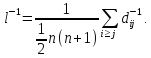
В выражении все
бесконечные значения
 никак не повлияют на результат, так
никак не повлияют на результат, так
 будет равно нулю [90, 91].
будет равно нулю [90, 91].
В вышеуказанном
контексте существование «эффекта малого
мира» означает, что распространение в
сети подобной реальному миру будет
зависеть от значения
 ,
и чем оно меньше, тем быстрее процесс
распространения по всей сети. Сейчас
«эффект малого мира» наблюдается, если
значение
,
и чем оно меньше, тем быстрее процесс
распространения по всей сети. Сейчас
«эффект малого мира» наблюдается, если
значение
 изменяется с логарифмической зависимостью
изменяется с логарифмической зависимостью
 ,
или медленнее.
,
или медленнее.
Свойство
транзитивности в виртуальных СИС иногда
также называют кластеризацией. Если в
графе точка
 взаимодействует с точкой
взаимодействует с точкой
 ,
и точка
,
и точка
 взаимодействует с точкой
взаимодействует с точкой
 ,
то существует высокая вероятность, что
точка
,
то существует высокая вероятность, что
точка
 взаимодействует с точкой
взаимодействует с точкой
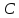 .
Другими словами: «друг твоего друга –
твой друг». Отсюда появляется возможность
разделить сеть на дизъюнктные группы
таким образом, чтобы было много ребер
внутри групп и мало ребер между группами.
.
Другими словами: «друг твоего друга –
твой друг». Отсюда появляется возможность
разделить сеть на дизъюнктные группы
таким образом, чтобы было много ребер
внутри групп и мало ребер между группами.
Транзитивность может быть определена как коэффициент кластеризации.

где:
 - количество «треугольников» графа;
- количество «треугольников» графа;
 - количество «вилок»
графа.
- количество «вилок»
графа.
Возможно вычисление коэффициента кластеризации через усреднение по вершинам, в этом случае:

где:
 - количество «треугольников» с вершиной
- количество «треугольников» с вершиной
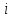 ;
;
 - число «вилок»,
центром которых является вершина
- число «вилок»,
центром которых является вершина
 .
.
Отсюда коэффициент кластеризации для всей сети равен:

Транзитивность
неориентированного графа может быть
также количественно оценена с помощью
коэффициента кластеризации, посчитанного
относительно единичной вершины.
Рассмотрим некоторую вершину
 ,
со степенью вершины
,
со степенью вершины
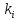 ,
обозначим как
,
обозначим как
 число ребер между
число ребер между
 вершинами соседними с
вершинами соседними с
 .
Тогда, коэффициент кластеризации
.
Тогда, коэффициент кластеризации
 вершины
вершины
 определяется как отношение числа
определяется как отношение числа
 к его максимально возможному значению
к его максимально возможному значению
 .
.

Фактически кластеризация способствует идентификации групп субъектов СИС.
Степень вершины
графа, характеризуется функцией
 ,
которая определяет вероятность того,
что случайно выбранная вершина будет
иметь ровно
,
которая определяет вероятность того,
что случайно выбранная вершина будет
иметь ровно
 ребер.
ребер.
Если в графе ребра
распределяются случайным образом,
большая часть вершин имеет приблизительно
одинаковую степень, близкую к средней
степени
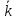 сети. Степени вершины случайного графа
нередко подчиняются распределением
Пуассона с пиком в
сети. Степени вершины случайного графа
нередко подчиняются распределением
Пуассона с пиком в


где:
 –
некоторый параметр распределения,
являющийся константой
–
некоторый параметр распределения,
являющийся константой
 –
степень;
–
степень;
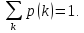
Однако для современных СИС, распределение степеней вершин является степенным. Такие сети называют сетями без масштабирования (безмасштабные сети)

где:
 – константа;
– константа;
 –
дзета-функция
Римана [29], которая служит, чтобы
выполнялось равенство
–
дзета-функция
Римана [29], которая служит, чтобы
выполнялось равенство
 .
.
Эффект «предпочтительного связывания» наблюдается, когда есть ребра, которые «чаще» соединяют вершины внутри одного типа, чем между разными типами.
Если
 – доля ребер между типами
– доля ребер между типами
 и
и
 в множестве всех ребер сети (
в множестве всех ребер сети ( ,
,
 ,
где
,
где
 -
число вершин в сети), то условную
вероятность того, что мой друг представляет
класс
-
число вершин в сети), то условную
вероятность того, что мой друг представляет
класс
 ,
при условии, что я сам представляю класс
,
при условии, что я сам представляю класс
 ,
можно выразить следующим образом
,
можно выразить следующим образом

Откуда эффект
«предпочтительного связывания» можно
измерить коэффициентом


Где деление на
 необходимо для нормировки коэффициента
необходимо для нормировки коэффициента

Этот коэффициент также способствует выявлению групп субъектов СИС на основе теории графов.
