10

Лабораторная работа №2

Сложение гармонических колебаний

Цель работы: Изучить биения и сложение двух взаимно перпендикулярных колебаний с помощью электронного осциллографа.

Оборудование и принадлежности: осциллограф универсальный

С1-65, звуковой генератор, соединительные провода.

ЭЛЕМЕНТЫ ТЕОРИИ

Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени. Простейшим типом колебаний являются гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса) и описываются уравнением типа

x = А соs (t + ₀),

где А – максимальное значение колеблющейся величины, называемое амплитудой колебания,  – круговая (циклическая) частота, ₀ или ₀ – начальная фаза колебания в момент t=0, (t + ₀) – фаза колебания в момент времени t. Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то х может принимать значения от +А до –А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемой периодом колебания, за который фаза колебания получает приращение 2.

Т= 2

Величина, обратная периоду колебаний,  = 1/Т называется частотой колебаний и равна числу полных колебаний, совершаемых в единицу времени. Откуда =2. Единица частоты  - герц (Гц). 1 Гц – частота периодического процесса, при которой за 1 с совершается 1 цикл процесса.

Гармонические колебания могут изображаться графически методом вращающегося вектора амплитуды, или методом векторных диаграмм.

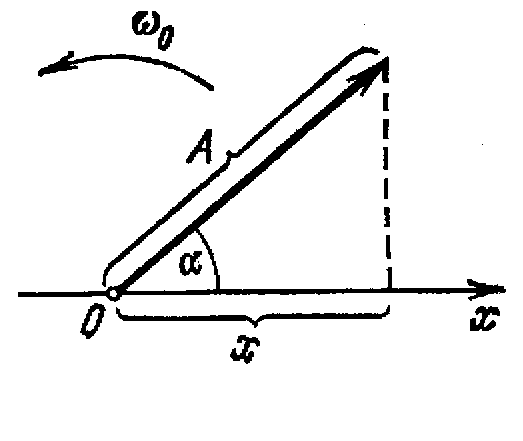Возьмем ось, вдоль которой будем откладывать колеблющуюся величину x (рис.1). Из взятой на оси точки О отложим вектор длины A, образующий с осью угол . Если привести этот вектор во вращение с угло­вой скоростью ω, то проекция конца вектора будет перемещать­ся по оси x в пределах от -А до +A, причем координата этой проекции будет изменяться со временем по закону

Рис. 1.

Следовательно, проекция конца вектора на ось будет совершать гармонические колебания с ам­плитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с на­чальной фазой, равной углу, образуемому вектором с осью в начальный момент времени.

Таким образом, гармоническое колебание может быть задано с помощью вектора, длина которого рав­на амплитуде колебания, а направление образует с осью x угол, равный начальной фазе колебаний.

Рассмотрим сложение двух гармонических коле­баний одного направления и одинаковой частоты. Результирующее колебание будет суммой колеба­ний х₁ и x₂, которые определяются функциями

, (1)

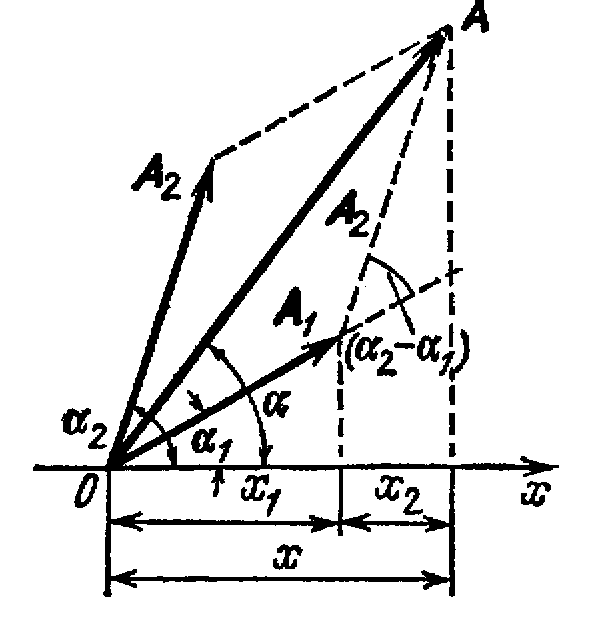¯ Представим оба колебания с помощью векторов A₁ и А₂ (рис.2). Построим по правилам сложения векторов результирующий вектор А. На рисунке вид­но, что проекция этого вектора на ось x равна сум­ме проекций складываемых векторов:

Поэтому вектор A представляет собой резуль­тирующее колебание. Этот вектор вращается с той же угловой скоростью ω₀, как и векторы А₁ и А₂, так что сумма x₁ и х₂ является гармоническим колебанием с

Рис. 2. частотой ω₀, амплитудой A и начальной

фа­зой α.

Используя теорему косинусов получаем, что

(2)

Также из рисунка видно, что

(3)

Представление гармонических колебаний с помощью векторов позволяет заменить сложение функций сложением векторов, что значительно проще.