1.5. Устойчивость активных электрических цепей. Критерии устойчивости.

Неустойчивость может наблюдаться в активных электрических цепях с обратными связями. В этих цепях энергия, накапливаемая пассивными элементами при переходном процессе, восполняется управляемыми источниками, что может привести к неограниченному росту напряжений и токов при ограниченном внешнем воздействии.

Анализ устойчивости производится по расположению корней характеристического полинома знаменателя передаточной функции исследуемой цепи на комплексной плоскости. При этом можно непосредственно находить значения корней (полюсов передаточной функции) или воспользоваться для этой цели критериями устойчивости. Рассмотрим оба подхода для анализа устойчивости на примерах.

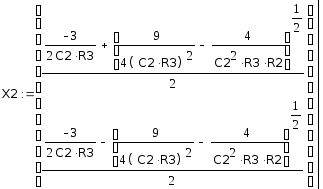
Для определения полюсов передаточной функции необходимо характеристический полином передаточной функции каждого звена электрического фильтра приравнять к нулю и найти их корни.

Характеристический полином передаточной функции (5) первого звена фильтра приравняем к нулю и найдем его корни :

12

Знаменатель передаточной функции (6) второго звена фильтра приравняем к нулю и решим полученное уравнение:

Если электрическая цепь устойчива, то все полюса будут расположены в левой полуплоскости комплексной плоскости ( рис.7).

Теперь исследуем устойчивость фильтра с использованием критерия Найквиста. Критерий устойчивости Найквиста применяется к электрическим цепям с обратной связью. Его можно сформулировать в геометрической трактовке так: система с обратной связью будет устойчивой, если годограф комплексной передаточной функции по петле обратной связи не охватывает точку с координатами (+1;j0), где - передаточная функция усилителя; - передаточная функция цепи обратной связи.

Построим годограф передаточной функции по петле обратной связи для первого звена фильтра. Для определения передаточной функции разорвем цепь обратной связи на входе усилителя и замкнем входные полюса первого звена фильтра. В результате получим расчетную схему, приведенную на рис.8. Комплексная передаточная функция по петле обратной связи для нее равна:

13

(16)

Составим узловые уравнения для узлов 1 и 2:

,

.

Рис. 7

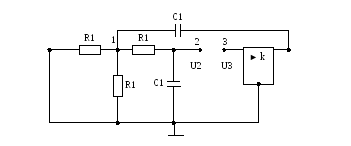
Рис. 8

14

Решив систему узловых уравнений, найдем выражение для передаточной функции (16) в следующем виде:

(17)

С помощью среды MathCAD построим годограф по петле обратной связи первого звена фильтра (рис. 9).

Рис. 9

Поскольку годограф не охватывает точку (1; j0), то по критерию Найквиста данная цепь устойчива. Максимум передаточной функции приходится на частоту :

Если посмотреть на годограф, то видно, что для устойчивости цепи коэффициент усиления должен быть k<4. Если же k=4, то звено фильтра будет находиться строго на границе устойчивости, при этом частота свободных колебаний будет .

15