ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра электротехники

ОБЩАЯ ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА

ИССЛЕДОВАНИЕ АКТИВНЫХ RC-ФИЛЬТРОВ

Методические указания и задания к курсовой работе

Факультет: электроэнергетический

Специальность: 220201-управление и информатика в технических системах

Вологда 2005

УДК 621. 372. 032

Общая электротехника и электроника. Исследование активных RC-фильтров. Методические указания и задания к курсовой работе. – Вологда: ВоГТУ, 2005г. – 31c.

Приведены краткие теоретические сведения, методические указания и варианты заданий к курсовой работе.

Утверждено редакционно-издательским советом ВоГТУ

Составители: В.В. Реутов, кандидат технических наук, доцент

Г.Л. Ганичев, кандидат технических наук, доцент

Рецензент: Н.А. Сердюков, кандидат технических наук, доцент

ВВЕДЕНИЕ.

Настоящие методические указания предназначены для студентов дневной и заочной форм обучения электротехнических специальностей, изучающих курс «Общая электротехника и электроника» и содержат краткие теоретические

сведения, задание и варианты по курсовой работе «Исследование активных RC-фильтров».

Содержание методических указаний соответствует государственному образовательному стандарту специальности 220201.

Целью курсовой работы является обучение студентов методам расчета электрических цепей с активными элементами и анализа свойств активных фильтров с использованием частотных характеристик передаточных функций, переходных характеристик и критериев устойчивости.

Ограниченный объем методических указаний не позволяет представить в них полные теоретические сведения по разделам курсовой работы. Студентам необходимо перед выполнением работы изучить соответствующий заданию теоретический материал, используя для этого конспект лекций и приведенный в указаниях список литературы.

Количество вариантов позволяет преподавателю выдать каждому студенту индивидуальное задание, что создает условия для самостоятельного выполнения курсовой работы и эффективного закрепления тех знаний, которые студент получает на лекциях и практических занятиях.

В целях снижения затрат времени на расчет и построение графиков можно использовать при выполнении работы пакеты прикладных программ, например, Mathcad.

1. Краткие теоретические свдения.

1.1.Особенности формирования узловых уравнений электрической цепи с идеальными усилителями.

Расчет передаточной функции фильтра производится путем формирования и решения узловых уравнений в операторной форме. Формирование уравнений электрической цепи с идеальными усилителями имеет следующие особенности:

- при формировании уравнения для входного узла влияние усилителя не учитывается, так как ток во входной ветви идеального усилителя равен нулю;

- для выходного узла узловое уравнение не может быть составлено, так как при нулевом выходном сопротивлении идеального усилителя его выходная проводимость равна бесконечности;

3

- систему узловых уравнений необходимо дополнить уравнением связи входного и выходного напряжений усилителя в результате получим систему, в которой число уравнений равно числу неизвестных.

Напряжение на входе и выходе усилителя с конечным коэффициентом усиления связаны уравнением:

, где

-операторное напряжение на входе ;

-операторное напряжение на выходе;

-коэффициент усиления.

Если коэффициент усиления задан равным бесконечности, то при конечной величине напряжения систему узловых уравнений необходимо дополнить уравнением:

=

При анализе цепей с дифференциальным операционным усилителем с бесконечным коэффициентом усиления система узловых уравнений должна быть дополнена уравнением:

=, где

- операторное напряжение на неинвертирующем входе усилителя;

-операторное напряжение на инвертирующем входе усилителя.

1.2.Операторная передаточная функция и ее частотные характеристики.

Операторной передаточной функцией называется отношение изображений выходного и входного напряжений (или токов). Для рассматриваемой в курсовой работе электрического фильтра передаточная функция имеет вид:

, где

-передаточная функция фильтра;

-передаточная функция по напряжению первого звена фильтра;

-передаточная функция по напряжению второго звена фильтра.

Рассмотрим порядок расчета передаточной функции одного звена электрического фильтра, например, первого.

4

Принципиальная схема электрической цепи звена представлена на рис.1.

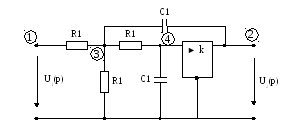
Рис. 1

Запишем узловые уравнения 1-го звена в общем виде. Для расчета передаточной функции достаточно записать уравнения для узлов (3) и (4):

(1)

(2)

Как было отмечено, в электрических цепях, содержащих идеальные усилители, узловое уравнение для выходного узла не составляют. Вместо этого рекомендуется использовать уравнение:

(3)

Расчёт коэффициентов левой части уравнений (1) и (2):

, , , ,

Расчёт правой части уравнений:

,

С учётом найденных коэффициентов, уравнения ( 1) и (2) примут вид:

.

5

В результате решения уравнений найдем передаточную функцию звена:

(4)

Преобразуем выражение для передаточной функции. С этой целью разделим числитель и знаменатель на коэффициент при операторе :

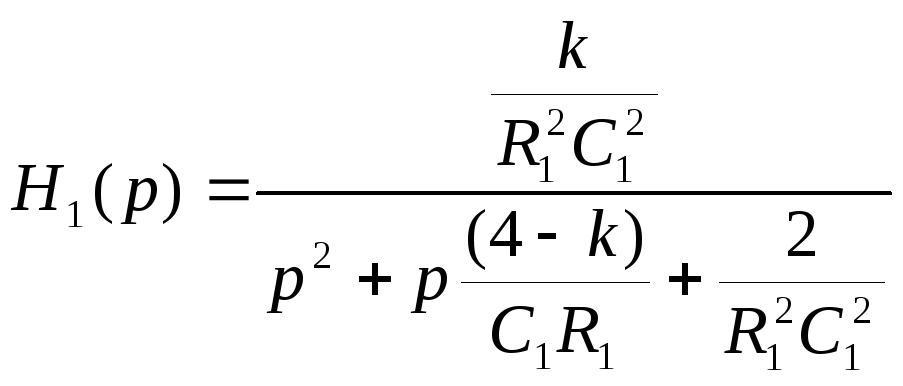(5)

Знаменатель передаточной функции звена содержит характеристический полином второго порядка, формально совпадающий с характеристическим полиномом резонансного колебательного контура.

,

где и - резонансная частота и добротность контура соответственно.

Аналогичные коэффициенты знаменателя передаточной функции звена называются добротностью и частотой полюса :

В таком же порядке производится расчет передаточной функции второго звена фильтра (рис. 2).

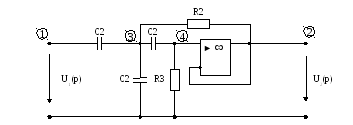
Рис. 2

6

Передаточная функция второго звена:

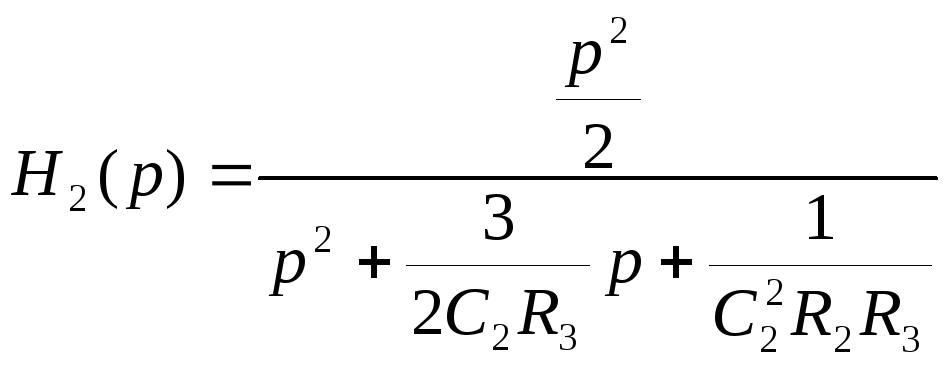(6)

- частота полюса второго звена;

- добротность второго звена.

Передаточная функция фильтра при каскадном соединении звеньев:

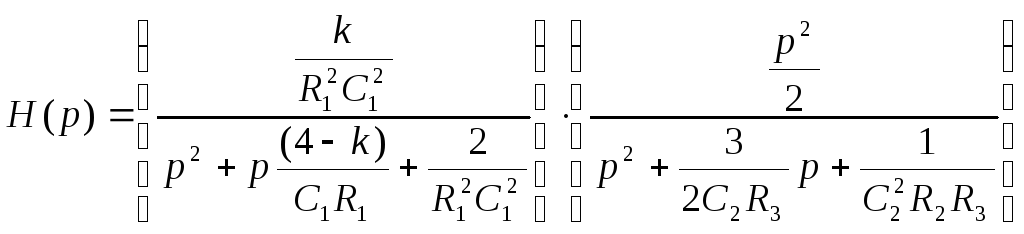(7)

При анализе процессов преобразования сигналов электрическими фильтрами представляет интерес исследования передаточной функции фильтра от частоты. График зависимости модуля передаточной функции от частоты называется амлитудночастотной характеристикой (АЧХ), а график зависимости аргумента – фазочастотной характеристикой (ФЧХ). Обе зависимости, построенные в широком диапазоне частот, определяют характер преобразования сигналов и тип фильтра: фильтр нижних частот (ФНЧ), фильтр верхних частот (ФВЧ), полосовой фильтр (ПФ), заграждающий фильтр (ЗФ) и другие типы фильтров с более сложным видом частотных характеристик.

Выражения для частотных характеристик передаточной функции фильтра получим на основании (7), подставив в него

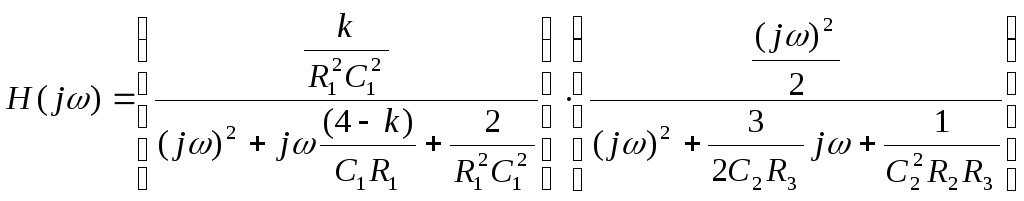(8) ,

H(j) – комплексная передаточная функция фильтра.

Расчет выражений для АЧХ и ФЧХ передаточной функции H(j производится в обычном порядке, как расчет модуля и аргумента комплексного числа.

График АЧХ передаточной функции изображают как в линейном, так и в логарифмическом масштабах. На оси ординат графика АЧХ , построенной в

7

линейном масштабе указывают модуль |H(j|. На оси ординат графика АЧХ,

построенной в логарифмическом масштабе, принято откладывать значение 20lg|H(j|. Эта величина оценивается в децибелах.

Фазовый сдвиг на фазочастотных характеристиках откладывают в линейном масштабе.

На рис.3 и рис.4 представлены графики АЧХ передаточной функции фильтра соответственно в линейном и логарифмическом масштабах. Фазочастотная характеристика передаточной функции приведена на рис.5.

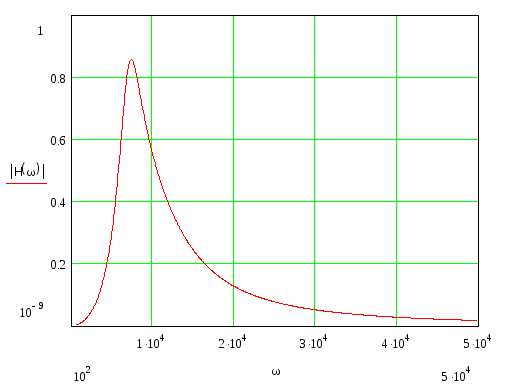
Рис. 3

По графикам можно сделать вывод, что АЧХ и ФЧХ передаточной функции при каскадном соединении первого и второго звена соответствуют частотным характеристикам полосового фильтра.