-
Контрольные вопросы и упражнения
-
Дайте определение выборки (выборочной совокупности).
-
Что называется объемом выборки?
-
По выборочным данным:
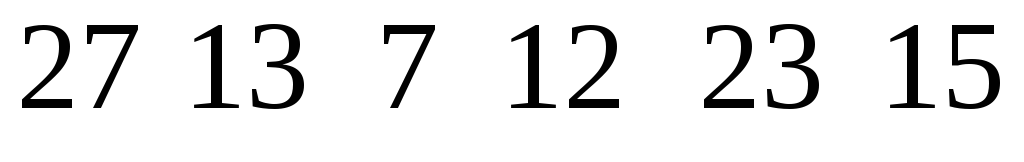составьте вариационный ряд. Укажите
объем выборки, размах выборки. -
Как построить интервальный статистический ряд?
-
Как найти частоты попадания в интервал?
-
Как найти относительные частоты?
-
Как построить гистограмму?
-
Как построить группированный статистический ряд на основе интервального?
-
Как построить полигон (полигон абсолютных частот)?
-
Постройте интервальный статистический ряд с 4 интервалами по выборочным данным: 4 12 8 4 8 3 4 1 3 2 3 13 4 7 6 2 8 5 3 7.
-
Постройте гистограмму относительных частот по статистическим данным.
-
Интервалы
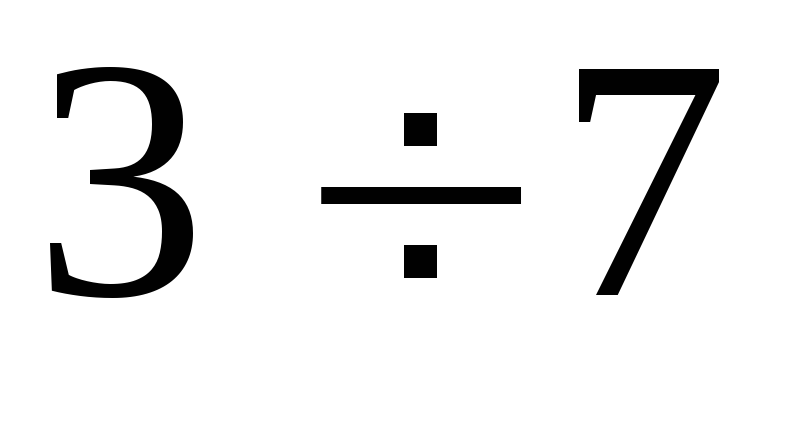
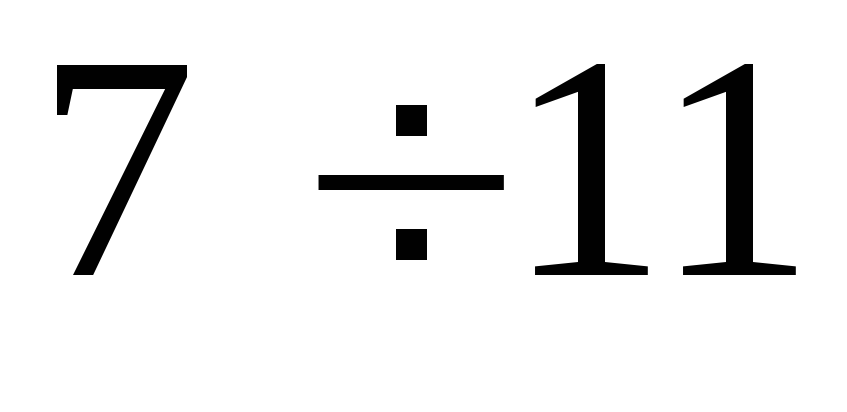
Частоты
4
5
8
3
-
Постройте группированный статистический ряд по статистическим данным.
-
Интервалы
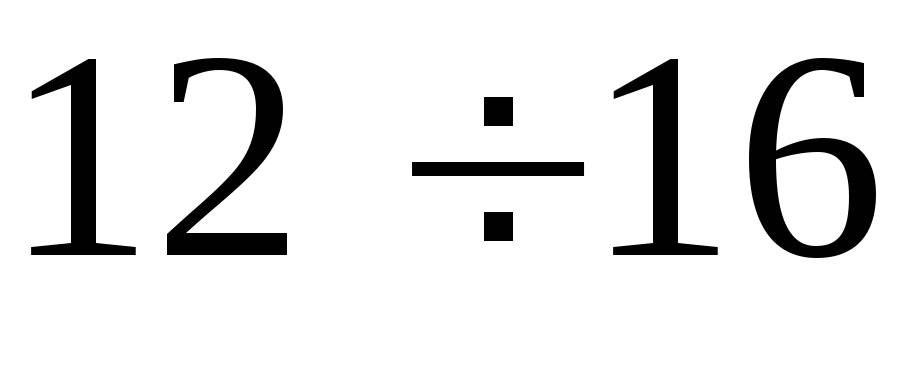
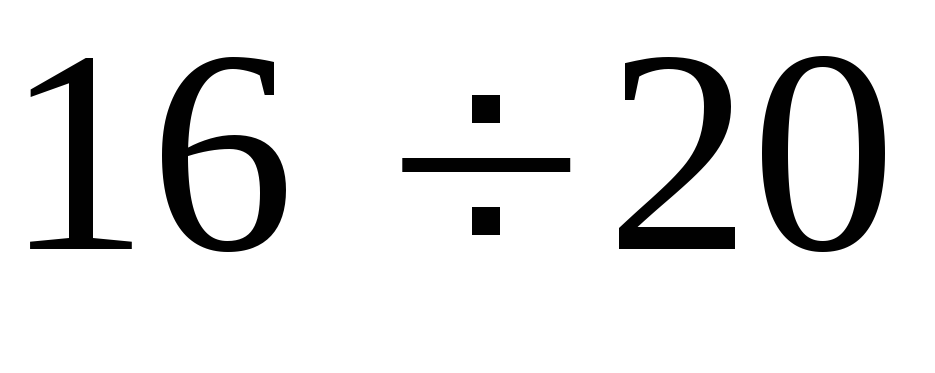
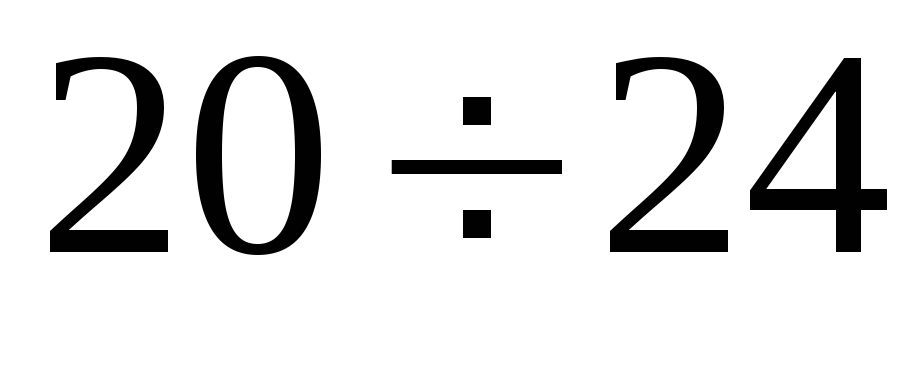
Частоты
6
11
8
5
-
Как по выборочным данным находится выборочная средняя?
-
Найдите выборочную среднюю по статистическим данным.
-
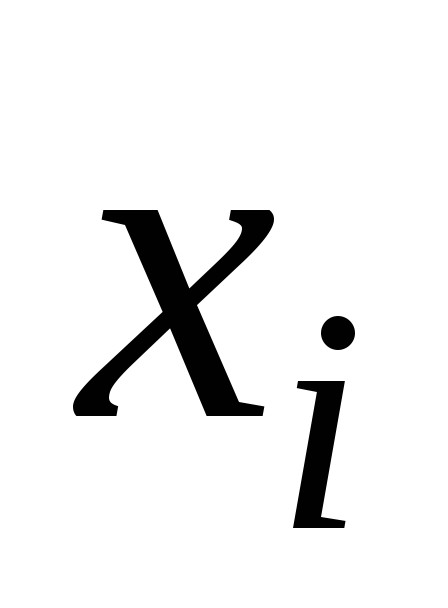
1
2
4
6
3
1
-
Как по выборочным данным находится исправленная выборочная дисперсия и выборочное среднее квадратическое отклонение?
-
Найдите исправленную выборочную дисперсию и выборочное среднее квадратическое отклонение по статистическим данным.
-
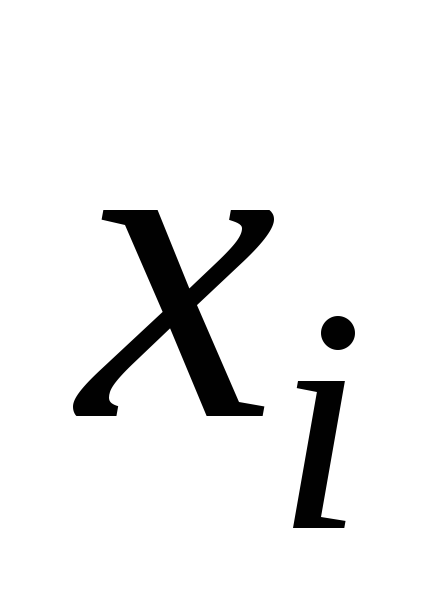
1
2
4
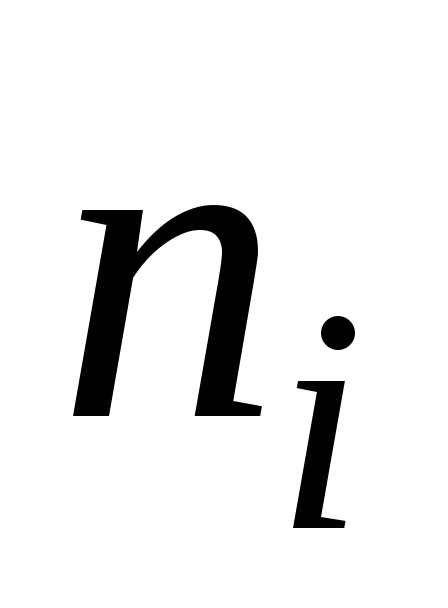
6
3
1
-
Проведя предварительную группировку, найдите коэффициент вариации выборочных данных: 2 1 5 5 3 2 1 3 1 1.
-
Найдите моду и медиану выборки.
-
1
3
5
7
9
3
8
6
2
1
-
На основе статистических данных
-
Интервалы
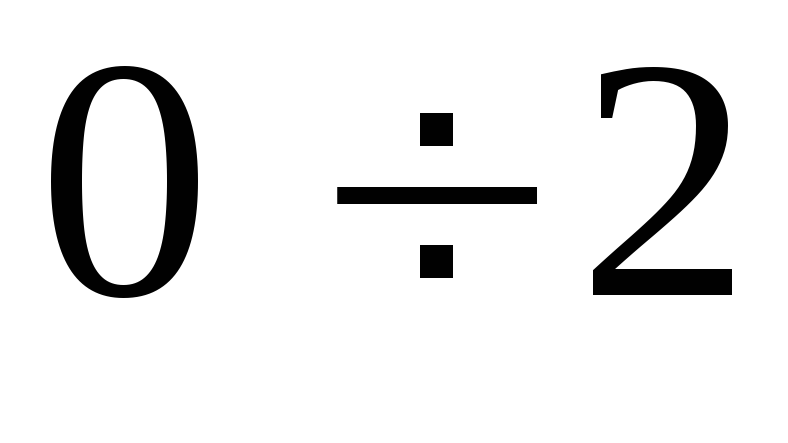
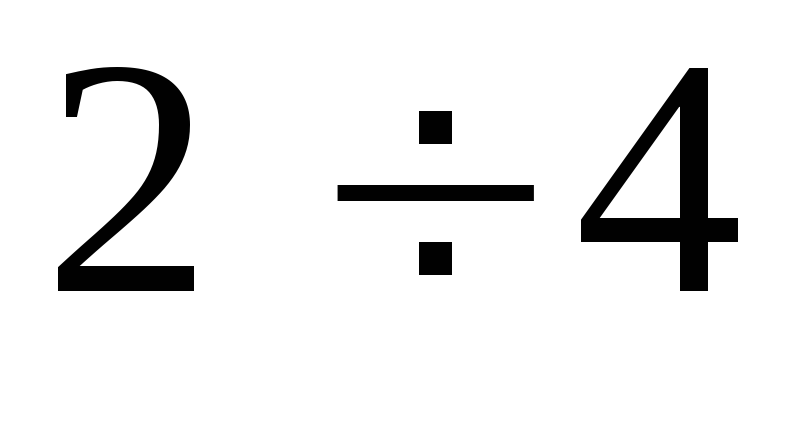
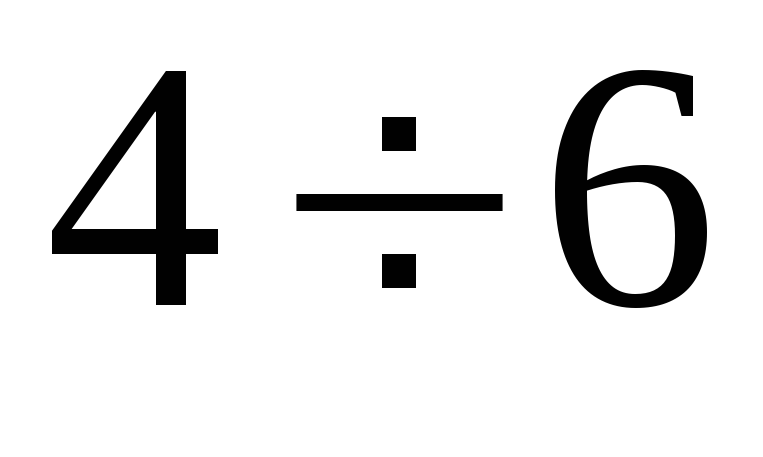
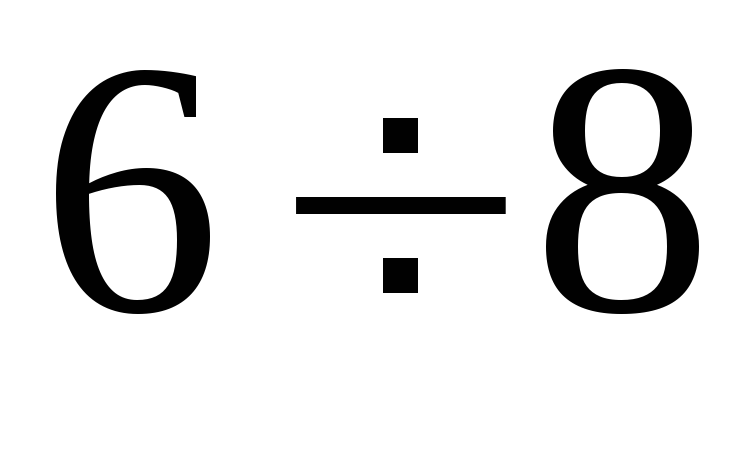
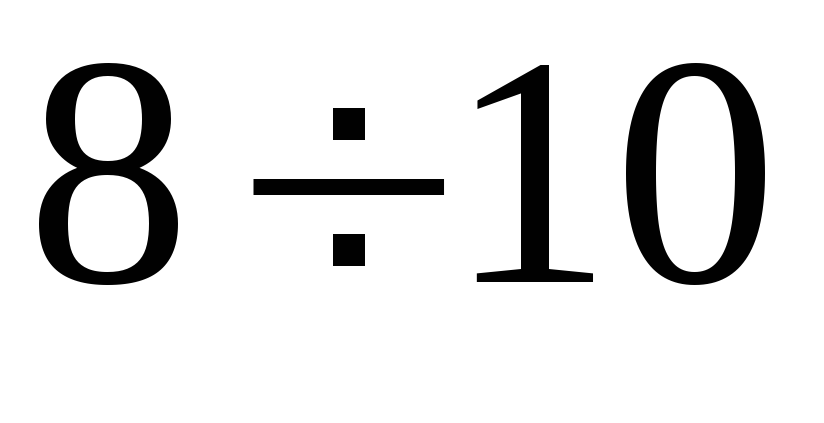
Частоты
12
6
4
2
1
выдвините гипотезу о типе распределения генеральной совокупности. Найдите параметры распределения.
-
На основе статистических данных
-
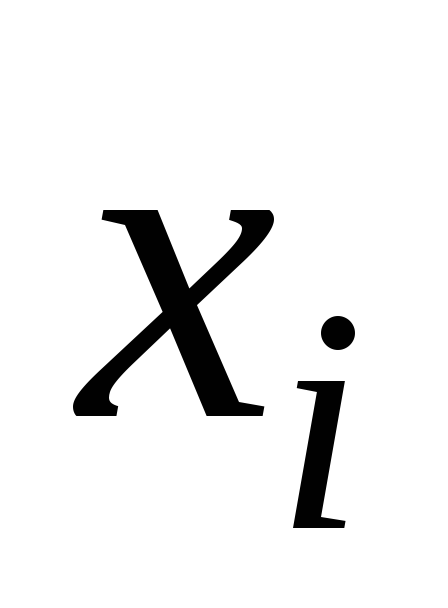
-1
0
1
2
3
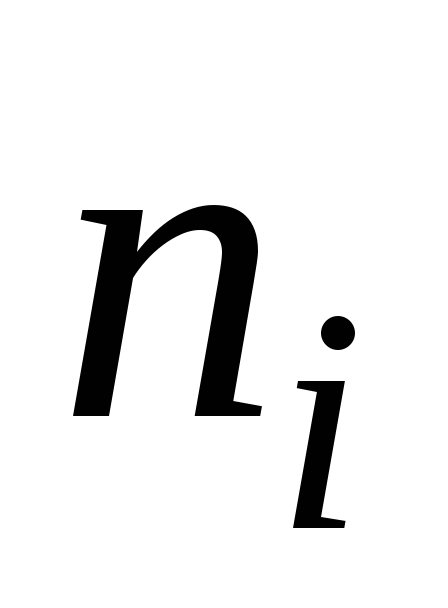
1
3
9
4
3
выдвините гипотезу о типе распределения генеральной совокупности. Найдите параметры распределения.
-
На основе статистических данных
-
Интервалы
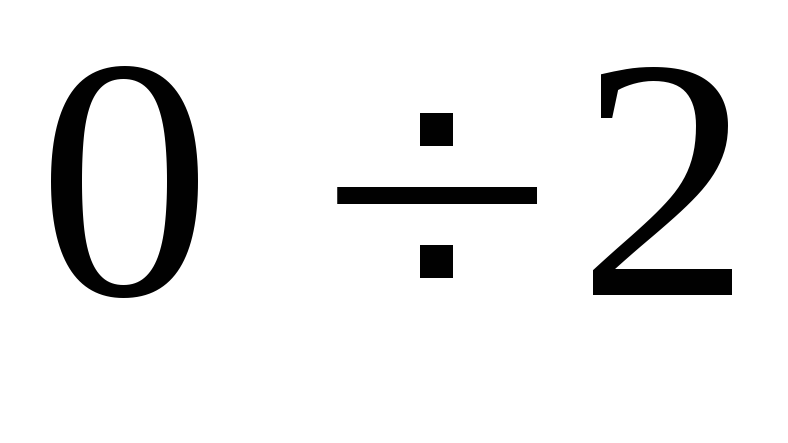
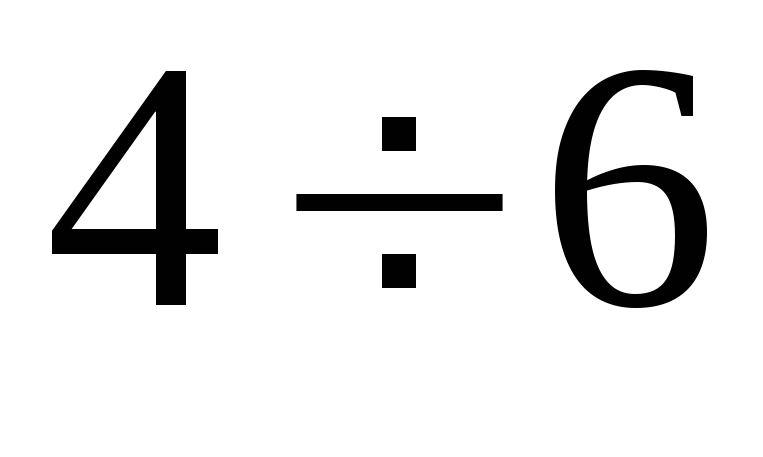
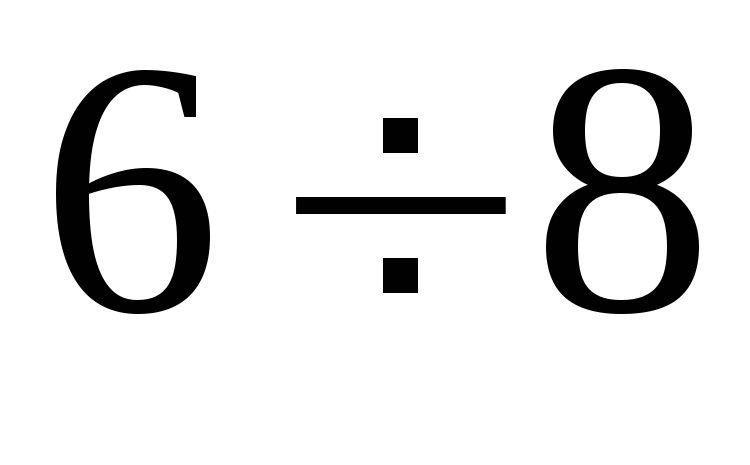
Частоты
12
5
2
1
получено теоретическое
распределение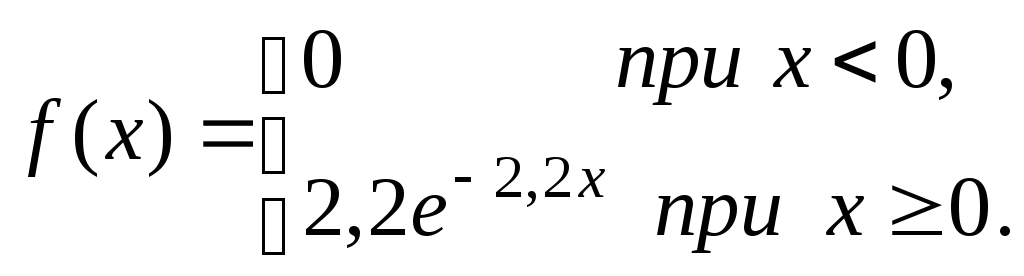
Найдите теоретические частоты попадания выборочных данных в интервалы статистического ряда.
-
При уровне значимости
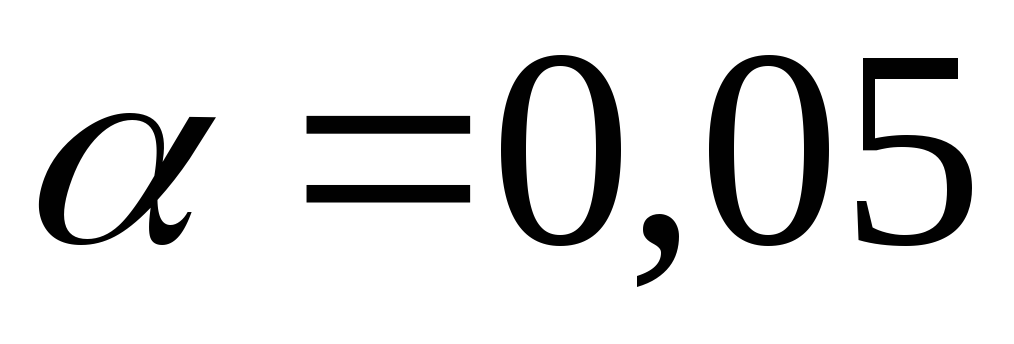проверить гипотезу о нормальном
распределении генеральной совокупности,
если известны эмпирические и теоретические
частоты.
-
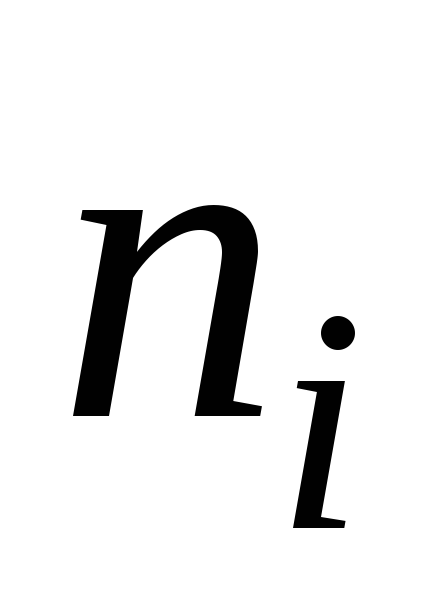
12
5
2
1
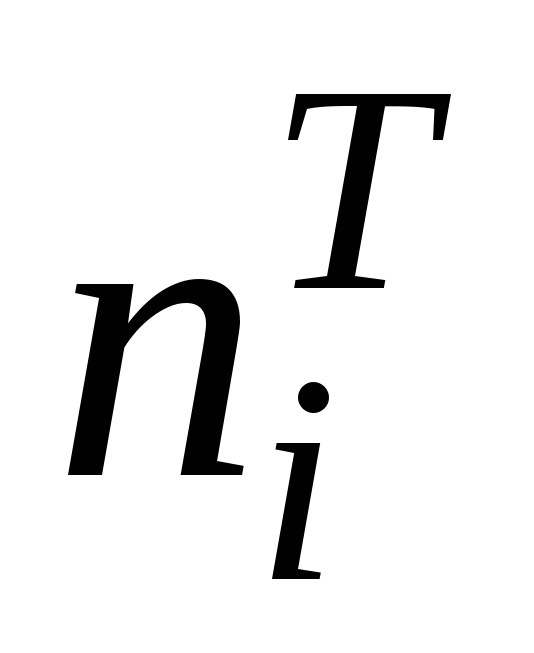
4
6
6
4