
- •Тема 1. Дискретна випадкова величина та закон її розподілу
- •Способи задання дискретних випадкових величин
- •Тема 2. Числові характеристики дискретних випадкових величин та їх властивості
- •Математичне сподівання та його основні властивості.
- •Основні властивості математичного сподівання
- •1) Математичне сподівання постійної величини дорівнює самій постійній
- •2) Постійний множник можна виносити за знак математичного сподівання
- •3) Математичне сподівання добутку декількох взаємно незалежних дискретних випадкових величин дорівнює добутку їх математичних сподівань, тобто
- •4) Математичне сподівання суми випадкових величин дорівнює сумі їх математичних сподівань, тобто
- •Дисперсія та її властивості.
- •Основні властивості d(X).
- •Середнє квадратичне відхилення дискретної випадкової величини.
- •Тема 3. Уявлення про закон великих чисел
- •Тема 4. Поняття про статистику та її методи
- •Джерела даних у статистиці
Дисперсія та її властивості.
Математичне сподівання характеризує центр розподілу дискретної випадкової величини. Але цієї характеристики недостатньо, бо можливе значне відхилення можливих значень від центру розподілу. Для характеристики розсіювання можливих значень X відносно центру розподілу введемо нову числову характеристику.
Означення 2. Дисперсією дискретної випадкової величини X називають число, яке дорівнює математичному сподіванню квадрата відхилення ДВВ X від її математичного сподівання.
Дисперсію величини X позначають D(X) або DХ. Це означення математично виглядає так
D(X)=M((X-М(Х))2). (2)
Основні властивості d(X).
1) Дисперсія будь-якої ДВВ X невід'ємна
D(X)>0
Дійсно, (X-М(Х))2 невід'ємна, тому згідно означення математичного сподівання та властивостей імовірностей рk, k=1,2,...,п, D(X) також невід'ємна.
2) Дисперсія постійної величини С дорівнює нулеві
D(C)=0.
Дійсно, якщо X=С, то М(С)=С, тому С-М(С)=0.
3) Постійний множник С можна виносити за знак дисперсії, при цьому постійний множник треба піднести у квадрат
![]() (3)
(3)
Дійсно, СХ-М(СХ)=С(Х-М(Х)), тому
![]()
Постійний множник С2 можна виносити за знак математичного сподівання, тому з формули (2) випливає потрібна рівність (3).
4) Дисперсія ДВВ X дорівнює різниці між математичним сподіванням квадрата випадкової величини X та квадрата її математичного сподівання
![]() (4)
(4)
Дійсно,
![]()
![]()
Зауваження 4. Формула (2) визначає дисперсію випадкової величини X, а за формулою (4) її доцільно знаходити.
5) Дисперсія алгебраїчної суми ДВВ X та У дорівнює сумі їх дисперсій
![]()
Доведення. Спочатку доведемо цю властивість для X+Y. Згідно з формулою (4) маємо
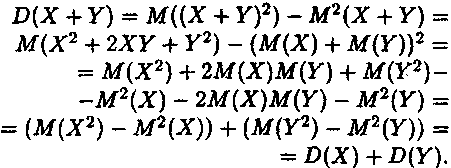
Тепер розглянемо дисперсію різниці X та Y
![]()
Зауваження 5. П'ята властивість дисперсії має місце для алгебраїчної суми не лише двох, але й скінченого числа дискретних випадкових величин.
Приклад 4. Знайти дисперсію випадкової величини X, що задана законом
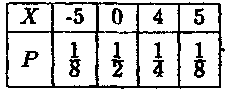
Розв'язання. Будемо шукати D(X) з використанням формули (4). Математичним сподіванням X згідно з формулою (1) буде
![]()
Щоб
знайти математичне сподівання X2,
тобто![]() ,
запишемо закон розподілу X2
у
вигляді таблиці
,
запишемо закон розподілу X2
у
вигляді таблиці
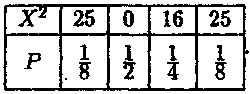
Відмітимо, що усі значення X2 отримані шляхом піднесення до квадрату відповідних значень X. Елементи другого рядка - імовірності цих значень - не змінюються.
За формулою (1) знаходимо
![]()
Згідно з формулою (4) тепер одержуємо
![]()
Середнє квадратичне відхилення дискретної випадкової величини.
У більшості випадків випадкова величина X має розмірність, наприклад, метр, міліметр, грам, тому її дисперсія D(X) буде вимірюватись у квадратних одиницях цієї розмірності.
У практичній діяльності доцільно знати величину розсіювання випадкової величини в розмірності цієї величини. Для цього використовують середнє квадратичне відхилення, яке дорівнює квадратному кореню з дисперсії і позначається
![]()
Тема 3. Уявлення про закон великих чисел
Припущення про існування ймовірності події, що нас цікавить, є гіпотезою, яка в кожному випадку вимагає спеціальної перевірки. Далеко не кожна подія з неоднозначним результатом (за незмінних умов випробування) має певну ймовірність.
Якщо
позначити статистичну частоту символом
 ,
де
,
де
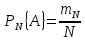 ,
то
,
то
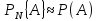 ,
де
,
де
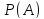 - ймовірність події А.
- ймовірність події А.
Індекс N ставиться спеціально, щоб підкреслити залежність статистичної частоти від кількості випробувань.
Ця наближена рівність, яка виражає властивість стійкості статистичних частот, багаторазово перевірена експериментально і підтверджена практичною діяльністю, є однією з найважливіших закономірностей масових випадкових подій. Математичне формулювання цієї закономірності вперше дав швейцарський математик Якоб Бернуллі у вигляді теореми.
Теорема. Якщо в ряді випробувань ймовірність деякої події залишається для кожного випробування сталою, то з достовірністю можна стверджувати, що при досить великій кількості випробувань статистична частота цієї події відрізнятиметься як завгодно мало від її ймовірності.
Теорема Бернуллі є простішою формою так званого закону великих чисел – одного з найважливіших законів теорії ймовірностей.
У теорії ймовірностей велике значення має з’ясування питання про те, наскільки частота може відхилятися від ймовірності. Таке відхилення вкаже на похибку, яка допускається, якщо прийняти частоту за ймовірність.
На можливості визначення величини відхилення частоти від ймовірності ґрунтується практичне застосування теорії ймовірностей в економіці, метеорології, медицини, біології, астрономії, теорії стрільби та багатьох інших галузях науки і практики.
Теорему
Бернуллі вперше було опубліковано в
1713 р. На доведення цієї «золотої теореми»,
як він її називав, було затрачено 20 років
життя вченого. Доведення Я. Бернуллі
ґрунтувалося на розгляді поведінки
біноміальних членів
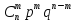 і займало 12 сторінок тексту.
і займало 12 сторінок тексту.
Надзвичайно коротке і строге доведення цієї теореми дав у 1845 р. російський математик П. Л. Чебишов.
У 1837 р. французький математик С. Пуассон довів теорему, яка узагальнює теорему Бернуллі на випадок, коли ймовірність події, що розглядається, змінюється в разі повторення випробувань.
Щоб
зрозуміти практичне значення наближеної
рівності
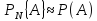 ,
розглянемо таку задачу.
,
розглянемо таку задачу.
Приклад. Виходячи з даних про народження дітей, можна зробити висновок: частота народжування хлопчиків у достатньо великій кількості спостережень за народжуваністю наближена до 0,511. Тому це число і береться за ймовірність події «народився хлопчик». На основі цієї ймовірності робиться демографічний прогноз.
