2.3. Игры.

Пусть есть n игроков, X₁,X₂,…,X_nмножества их стратегий, f₁(x),…, f_n(x)  их функции выигрыша, x=(x₁,…,x_n)совокупная стратегия игроков и x_jX_{i ,}.

Принципы рационального поведения в играх:

1. Принцип Парето xy, если i f_i (x)  f_i (y)   i₀: f_i0 (x)  f_i0 (y).

2. Принцип пессимиста: он считает, что цель соперниковнавредить ему 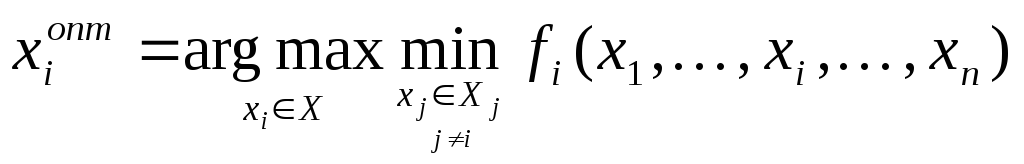 . Стратегия называется максиминной.

3. Принцип равновесия (Нэша): совокупная стратегия x*=(x₁*,…,x_n*) оптимальна по Нэшу (равновесна), если всем игрокам невыгодно отступать от своих частей совокупной стратегии, т.е. i f_i (x*)  f_i (x₁*,…,x_i,…,x_n*).

Пример Гермейера: nигроков, множества стратегий X_i=[0,1], функции выигрыша: . Оптимальной по Нэшу и максимину является стратегия, при которой все выбирают 1 и выигрывают 1. Оптимальными по Парето являются стратегии, когда все выбирают 0 и выигрывают n-1, или когда i-й игрок выбирает 1,а остальные – 0; при этом i-й получает n, а остальные – n-2.

№12. Биматричная игра

Число игроков = 2, множества стратегий конечны. Функции выигрыша = две матрицы. Один игрок выбирает номер строки матриц, другой  номер столбца.

Пример: Пусть. fx_ij=f_x(x_i,y_j) – выигрыш игрока х, если он играет по x_i ,а y по y_j .

fx	y1	y2	miny		fy	y1	y2	maxy
x1	5	1	1		x1	3	3
x2	2	6	2		x2	4	5
x3	1	4	1		x3	8	2
maxx			=2		minx	3	2	=3

1. максиминные стратегии существуют всегда:

x^опт=argmax{min f_x(x_i,y_j)} = x₂ y^опт=argmax{min f_y(x_i,y_j)} = y₁

x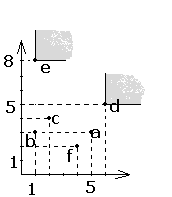_i y_j y_j x_i

2. оптимальны по Парето только совокупные стратегии {( x₂ ,y₂), (x₃ ,y₁)}:

в правом верхнем квадранте от них нет других точек.

Точки с максимальными координатами f_x и f_y всегда оптимальны по Парето.

3. Н эш. Рассмотрим условные оптимумы:

x^опт(y) = argmax_x f_x(x,y), y^опт(x) = argmax _y f_y(x,y). Представим эти функции в виде двудольного орграфа. Оптимуму по Нэшу соответствует неориентированное ребро.

Таких может не быть. У нас – это ребра {( x₁ ,y₁), (x₂ ,y₂)} .

Заметим, что оптимумы по Нэшу и по Парето не совпали.

Def: Играантагонистическая, если увеличение выигрыша одного из игроков ведет к уменьшению выигрыша другого (интересы противоречивы). Если f_x(x,y)+f_y(x,y)=const, то игра – с постоянной суммой (в т.ч. с нулевой).

Лемма 1: Пусть x [ f₁(x)  f₂(x) ], x₁=arg max f₁, x₂=arg min f₂.

 max f₁ (x)= f₁ (x₁) f₂ (x₁) max f₂ (x), min f₁ (x) f₁ (x₂) f₂ (x₂)= min f₂ (x).

Лемма 2: Пусть f₁ (x) + f₂ (x)=0, т.е. f₂ (x) = f₁ (x) x.

 max f₂ (x)=max {f₁ (x)}=min f₁  arg max f₂=arg min f₁.

№13. Матричные игры.

Игра двух лиц с конечными множествами стратегий и нулевой суммой, когда f₁+f₂=0, задается одной матрицей. Пусть Z* - множество всех совокупных стратегий, оптимальных по Нэшу; Z^опт – множество оптимумов по максимину.

1. Оптимальными по Парето являются все совокупные стратегии.

2. Z^опт  , т.е оптимум по максимину существует всегда.

3. Z*   Z^опт.= Z*, т.е. оптимум по Нэшу может не существовать, но если он существует, то совпадает с оптимумом по максимину.

Лемма 3: Пусть ,  v₁ ≤ v₂  f.

Доказательство: Имеем и по лемме 1 



Числа v₁ и v₂ называются нижним и верхним значениями игры.

Теорема: Утверждения Z* , v₁=v₂ и Z* = Z^опт эквивалентны, т.е. матричная игра имеет решение по Нэшу тогда и только тогда, когда v₁=v₂. При этом оптимумы по максимину и по Нэшу совпадают.

Доказательство. 1) Пусть (x*,y*)  Z*, т.е.  т.е. v₂< v₁. Но по лемме 3 v₁< v₂ ,  v₂ = v₁ и все неравенства суть равенства  и , т.е. Z*  Z^опт.

2) Пусть v₁=v₂ и , . Тогда , т.е. для всех x и y. Полагая сначала x=x^опт, а потом y=y^опт, получим Z^опт  Z*, т.е. любое решение по максимину оптимально по Нэшу  Z* .

5	4	3	3
6	1	2	1
0	5	1	0
6	5	3

Оптимум по Нэшу оптимален по всем критериям рационального поведе­ния и называется решением игры в чистых стратегиях. Условием его сущест­вования является равенство v₁=v₂=v, а само число v называют значением игры.

	y1	y2	y3	miny
x1	3	6	2	-6
x2	1	4	3	-3
maxx	3	4	2

Пример1: v₁ = v₂ = v=3. Решение игры - x^опт=x₁, y^опт=y₃. Кстати,

цикл x₂  y₂  x₃  y₁  x₂, но x₁  y₃. p=(0,¹/₂,¹/₂), q=(²/₅,³/₅,0)?

Пример2: x^опт=x₂, y^опт=y₃ , v₁ = -3 ≠ 2= v₂.

 решения в чистых стратегиях нет, его нужно искать в смешанных стратегиях.

Д

P1 Pn

оминирование: y₁>y₃  отбросим y₁ (с большим проигрышем)!

Игра в смешанных стратегиях.

Пусть {f_ij}  матрица игры размера nm, т.е. f_ij=f(x_i,y_j) – выигрыш игрока x, если он играет по стратегии x_i, а его соперник  по стратегии y_j. Смешанными стратегиями игроков назовем векторы p и q, задающие распределение вероятностей на множествах чистых стратегий игроков, т.е. p_i, q_j0, p_i=q_j=1. Разобьем один интервал [0,1] на n отрезков с длинами p₁,…,p_n, а другой - на m отрезков с длинами q₁,…,q_m . Датчиком равномерного распределения - функцией СлЧис() разыграем две случайных точки. Попадание в iый отрезок первого интервала (с вероятностью p_i) соответствует выбору стратегии x_i, в jый отрезок второго интервала (с вероятностью q_j) - выбору стратегии y_j. Свой выбор соперники осуществляют независимо друг от друга.

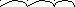
Посчитаем математическое ожидание выигрыша первого игрока:

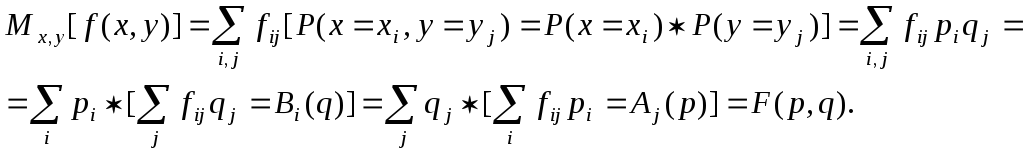
Определим и . Тогда

,

.

Сведение матричной игры к ЛП

Заметим, что . v v*=min A_j A_j Тогда

Нахождение v₁ является задачей линейного программирования, т.к. ограничения

и линейны относительно переменных v и p_i. Кроме того, задачей ЛП, двойственной к предыдущей, является нахождение v₂: .

Лемма 4: Матричная игра всегда имеет решение в смешанных стратегиях.

Т.к. значения функционалов в прямой и двойственной задачах ЛП совпадают, то в смешанных стратегиях v₁=v₂,  игра имеет решение по Нэшу.

Е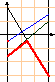сли p^опт найдена (например, графоаналитическим методом), то q^опт находят по теореме о доп. нежесткости: p_i(B_i(q)₂)=0, q_j(A_j(p)₁)=0.

Графоаналитический метод решения для игр 2n и n2

Пример:	q1	q2	q3	min		формула	p1: 0 1
p1	3	6	2	6		A1(p)=3p1-1p2 A2(p)=-6p1+4p2 A3(p)=2p1-3p2	1 4 3	3 6 2
p2	1	4	3	3
max	3	4	2	v1 < v2

Из графика (шаг сетки =2) видно, что A₁(p)>A₃(p) (доминирование),

максимум нижней огибающей лежит на пересечении прямых А₂ и А₃,

т.е. 6p₁+4p₂=2p₁3p₂  8p₁=7p₂. Но p₁+p₂=1  p^опт= (⁷/₁₅, ⁸/₁₅). Проверим:

A₁(p^опт) = ¹³/₁₅ > ²/₃ = A₂(p^опт) = A₃(p^опт)  нижняя огибающая в окрестности p^опт в самом деле сформирована прямыми А₂(p) и А₃(p). Производная огибающей меняет в точке  p^опт знак с + на - :  A₃'(p^опт) = 5, а A₂'(p^опт) = 10  p^опт является точкой max. Цена игры  = A₂(p^опт) = – ²/₃. Для нахождения q^опт графоаналитический метод неприменим: функции B_i(q) и их верхнюю огибающую сложно нарисовать (в равенстве q₁+q₂+q₃=1 две переменные свободны). Воспользуемся ТДН: p_i·[B_i(q)  v₂] = 0 = q_j·[A_j(p)  v₁]. A₁(p^опт) > v₁  q₁= 0, но p₁, p₂> 0  -6q₂+2q₃= B₁(q) = v₂= B₂(q) = 4q₂– 3q₃. 5q₃= 10 q₂, но q₂+q₃=1,   q^опт= (0, ¹/₃, ²/₃) и v₂= B₁(q^опт) = – ²/₃.

Замечание: Если матрица игры кососимметрична (т.е. квадратная и ƒ_ij=ƒ_ji), то игроки равносильны и их оптимальные стратегии совпадают.

 !!! При решении игр размера 2n алгоритмом Меджидо не нужно предварительно удалять доминируемые строки и столбцы (это требует O(n²) операций, а они удаляются алгоритмом автоматически), I^–= для p, I⁺=  для q, интервал [u₁,u₂] = [0,1] сразу.

Пример М3. v₁v₂  Решаем в смешанных стратегиях.

Пример:	Y1	Y2	Y3	Y4	min
X1	7	3	6	5	3
X2	2	4	8	3	2
X3	4	1	5	4	1
max	7	4	8	5

Доминирование: X₁ > X₃  отбрасываем X₃,

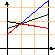
Y₃ > Y₂  отбрасываем Y₃ (больший проигрыш хуже)

A₁(p)=7p₁+2p₂ , Из графика получаем A₄= A₂,

A₂(p)=3p₁+4p₂, 5p₁+3p₂=3p₁+4p₂ 2p₁=p₂ , p₁+p₂ = 1

A₄(p)=5p₁+3p₂.  p₁= ¹/₃ , p₂= ²/₃.

v=A₄(p)=5p₁+3p₂= ⁵⁺⁶⁼¹¹/₃. A₁(p)=7p₁+2p₂ = v.  Все прямые пересекаются в точке.

Ищем q _опт по ТДН: p₁, p₂>0  B₁(q)=v=B₂(q) 7q₁+3q₂+5q₄=2q₁+4q₂+3q₄ q₁+q₂+q₄ =1 q₂ =5q₁ +2q₄  6q₁ +3q₄ = 1. q₄ = ¹/₃ - 2q₁ , q₂=5q₁ +2(¹/₃-2q₁) = ²/₃+q₁. q^опт= (q₁ , ²/₃+q₁ , 0, ¹/₃-2q₁)  0  q₁  [0, ¹/₆]

П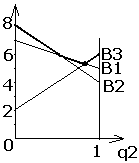ример М4: Задача проверки. Можно ли отбросить Y₁, полагая q₁ =0?

	Y1	Y2	Y3	Bi (q)
X1	3	5	7	B1=5q2+7q3
X2	2	4	8	B2=4q2+8q3
X3	1	6	2	B3=6q2+2q3.
X4	8	2	1	B4=2q2+q3.

Остается игра 2  3: X₄ < X₁  отбросим X₄.

B(q) - верхняя огибающая семейства прямых В_i., q^опт- точка минимума функции B, в ней B₃=B₁

 5q₂+7q₃ = 6q₂+2q₃ или q₂=5q₃. Но q₂+q₃ =1,

 q₂=⁵/₆ , q₃ = ¹/₆. q^опт =(0, ⁵/₆, ¹/₆), v = ³²/₆.

B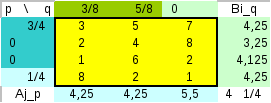₂(q) < v  p₂=p₄=0  5p₁+6p₃=7p₁+2p₃, p^опт=(²/₃,0,¹/₃, 0 ).

Но A₁(p) = ⁷/₃ < v  по ТДН это не решение игры  отбросить Y₁ нельзя.

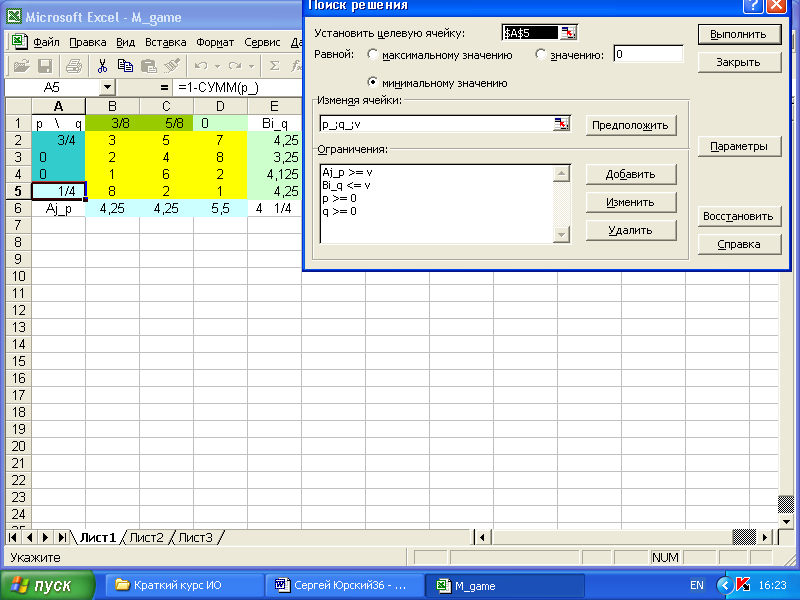
Эта игра легко решается в EXCEL командами Сервис+Поиск решения при следующих ограничениях:

В качестве параметра

выбираем тип модели – линейная.

p^опт=(³/₄,0,0,¹/₄), q^опт=(³/₈,⁵/₈, 0), v = 4¹/₄ .

Бесконечные антагонистические игры со счетным числом стратегий.

J\I	y1	y2	y3	…
x1	0	-1	-1	…
x2	1	0	-1	…
x3	1	1	0	…
…	…	…	…	0

Если игроки имеют не конечное, а счетное число стратегий, то при  |a_ij| < , все теоремы с конечного случая переносятся на счетный.

Иначе возможны следующие «плохие» случаи.

Случай 1: . Члены ряда равномерно ограничены, в чистых стратегиях существуют maxmin и minmax, но .

Перейдем к смешанным стратегиям: , _n^p_k 0.

монотонно убывает по j и стремится к –1.

Т.о. не существует, но .

J\I	y1	y2	y3	…
x1	0	-1	-2	…
x2	1	0	-1	…
x3	2	1	0	…
…	…	…	…	0

Аналогично , , монотонно возрастает по i и стремится к +1. Т.о. не существует, но ..

Случай 2: . Члены ряда не ограничены, поэтому в чистых стратегиях maxmin и minmax не существуют, как и supinf и infsup. Если p = (½, ¼, 0, ⅛, 0, 0, 0, ¹/₁₆, …), т.е. p_i = {2^-(k+1) при i = 2^k

и 0 при i ≠ 2^k}, то вообще не имеет смысла.

.

№14. Игра на квадрате.

Игра с нулевой суммой, f(x,y)функция выигрыша первого игрока; x,y[0,1].

Чтобы существовали ₁ и ₂, достаточно, чтобы были выполннены условия:

1) f непрерывна; 2) f строго вогнута? по x, строго выпукла? по y.

Теорема: При выполнении условий 1-2 существует решение в чистых стратегиях.

Доказательство: Определим непрерывные (докажите!) функции .

Пусть x* неподвижная точка их непрерывной! суперпозиции, т.е. ((x*))=x*.

Обозначим y*=(x*)  (y*)=x* и y* неподвижная точка функции ((y)).

П окажем, что f(x,y*)f(x*,y*)f(x*,y):

(x*,y*) седловая точка (ситуация равновесия),  оптимальная стратегия.

Пример: f(x,y)= -2x²+y²+3xy-x-2y. Теорема применима. Найдем функции и .

Сначала найдем точки абсолютных max и min и проверим условие «[0,1]?».

∂f/∂x = -4x+3y-1=0  x_абс = ^3y-1/₄ [-¼,+½] при y[0,1].

А

(y)=	0	при y[0,⅓)	,	(x)=	2-3x/2	при x[0,⅔]
	3y-1/4	при y[⅓,1]			0	при x(⅔,1]

налогично, ∂f/∂y = 2y+3x-2=0  y_абс = ^2-3x/₂ [-½,1] при x[0,1] 

Предположим, что y* = ψ(x*)=0  х>⅔, но х*=  (y*) =  (0) = 0. Противоречие. Предположим, что х*=  (y*)=0  y<⅓, но y* = ψ(x*) = ψ (0) = 1. Противоречие.  Нужно брать функции  и  не по этим веткам.

 х* =  (y*) = (3y*-1)/4 при y⅓, но y* = ψ(x*) = (2-3x*)/2; получаем 17x*=4  x*=⁴/₁₇ y*=1-³/₂* ⁴/₁₇=¹¹/₁₇. Получили решение игры ( ⁴/₁₇, ¹¹/₁₇).

№15. Позиционные игры.

Def: Под позиционной игрой n лиц понимается:

1. ориентированное дерево Г с выделенным корнем А (Аначальная позиция, невисячие вершины  промежуточные позиции, а висячиезаключительные);

2. для висячих вершин заданы nмерные векторы выигрышей игроков;

3. задано разбиение невисячих вершин на n+1 подмножество очередности хода S_i, и в каждой вершине vS_i ход делает игрок с номером i (0 означает, что ход делается случайно);

4. для позиций из S₀ заданы распределения вероятностей на исходящих дугах;

5. задано разбиение S_i (i0) на информационные подмножества S_ij (S_i= S_ij), причем позиции одного информационного подмножества имеют одинаковое количество дочерних позиций; а материнские позиции находятся в разных информационных подмножествах с дочерними;

6. для каждой позиции sS_ij существует нумерация дочерних позиций, и ход игрока состоит в выборе номера дочерней позиции (даже не зная самой позиции, выбор будет однозначным).

Def: Игра называется игрой с полной информацией, если каждое информационное подмно­жество состоит из одной позиции, а случайный ход может быть сделан только из корня.

Пример игры с полной информацией. Одномастка.

Есть два игрока, стол и колода из 2n пронумерованных карт. Случайно карты разда­ются поровну между игроками и определяется ХОДЯЩИЙ игрок. Игроки знают свои карты  знают карты соперника, т.е. игра идет “в открытую”. ХОДЯЩИЙ выбирает и кладет на стол одну из своих карт, а соперник ОТВЕЧАЕТ своей. Хозяин старшей карты стола получает очко и право ХОДА, карты стола удаляются из игры. Цель игры – набрать максимум очков.

Каждой карте припишем индекс – разность числа своих и чужих карт; старших или равных этой карте. Пусть  – вектор индексов карт ХОДЯЩЕГО,  – вектор соперника. При оптимальной игре индексы, как правило, сохраняются. Правила редукции:

при ОТВЕТЕ рассматриваем только два варианта: бить (самой младшей бьющей картой–если есть) или отдать (самую младшую), причем если после взятия хозяин старшей карты не меняется, то ответ отдать отбрасываем;

при ХОДЕ отбрасываем мажорируемые по Парето карты (если их индекс не меньше & они младше), ход с одиночки (если это не самая младшая карта ХОДЯЩЕГО) и ход с туза (если остались другие варианты ХОДА). Двойные стрелки отмечают лучший ход. Жирные цифры помечают карты игроков, ? – варианты хода, * - ХОД, цифры внизу – последовательность ходов в игре без вариантов.

На этом построение дерева можно закончить. Число висячих вершин равно 4. (6!)² ≈500 000.

На дереве игры для S1 мы использовали процедуру  отсечений.

Сколько вообще может быть таких отсечений? Что такое - отсечение?

Объем дерева игры = mⁿ. Пусть есть кто-то, кто подсказывает вариант игры, тогда получим рекуррентное соотношение для трудоемкости:

T_n^сп=T_n1+(m1)T_n2; T_n^сп=O(n^(m+1)/2) для сокращенного перебора;

T^пп=mT_n1=m²T_n2=…=mⁿ для полного перебора.

Пример: n=10, m=7. Полный перебор требует 10⁷, а с α–β отсечениями 10⁴ операций.

Если цена игры одинакова при двух вариантах хода, надо учитывать, что соперник может сы­грать неверно. Поэтому выбирается ход, максимально обладающий "ловушечными" свойствами. Антиловушечный метод  игроки избегают ситуации, в которых сами могут сделать ошибку.

Игрок	Оптимальная игра игроков	Игра с ловушками	Игра с антиловушками
"+"	max	max	M(мат.ожидание)
""	min	M	min

Способы игры:

Интересные позиции:

+0110000111 – старшая единица активна (должна взять очко)  ход с нее плох – ее побьют.

+0110001011 – оба хода верные, но ход с младшей лучше – это «антиловушка».

+0110000101011011 – ход со старшей (активной) единицы плох – ей отдадут, но промежуточные карты уменьшат свой индекс и число активных карт уменьшится.

+011000111001 – просто интересная позиция. Верный розыгрыш – ход со старшей, бить, старшая (ловушка), отдать, старшая (ловушка), бить.

+110010110100, 100011001110, 1001011010, 1000111010, 0110011010, 10010101, 01100101.

Стратегии позиционной игры.

Def: Стратегия  это правило однозначного выбора хода в любой возможной позиции.

В терминах дерева игры стратегия iого игрока  это поддерево, в котором в позициях с ходом iого игрока есть только одна дочерняя, а в позициях с ходом других игроков  все дочерние из дерева Г. Число стратегий  число различных таких поддеревьев дерева игры.

Правило подсчета числа стратегий:

в позициях со своим ходом числа стратегий суммируют­ся,

а в позициях с ходом соперника - перемножаются.

Пример: Посчитаем число стратегий в игре «крестики - нолики» размера 3*3.

S₉ – число стратегий игрока, делающего первый ход.

= 9 ветвей, их нужно суммировать. Затем ходит соперник  умножаем.

S₉=9*S₇⁸, S₇=7* S₅⁶, S₅=5*S₃⁴, S₃=3*S₁², S₁=1

S₉=9*(7*S₅⁶)⁸=9*7⁸*S₅^6*8=9*7⁸*5^6*8*S₃^4*6*8=9*7⁸*5^6*8*3^4*6*8*1^2*4*6*8

Теорема: Любая позиционная игра с полной информацией при сведении ее к матричной игре имеет седловую точку (т.е. решение в чистых стратегиях).

Практически это никогда не делается, т.к. число стратегий очень большое.

№16. Коалиционные игры.

При числе игроков больше двух задаются функции выигрыша всех игроков. Для игры трех лиц используем обозначения без индексов: xX, yY, zZ f_x(x,y,z), f_y(x,y,z), f_z(x,y,z).: Пусть - максиминные стратегии игроков (при этом каждый игрок считает, что он в одиночку играет против всех остальных). Если игроки Y и X образуют коалицию и согласовывают все свои действия, их рассматривают как одного игрока со стратегиями w=(x,y)W=XY и функцией выигрыша f_w(x,w) = f_y(x,y,z) + f_z(x,y,z). Максимальные выигрыши, на которые могут рассчитывать игроки y и z, играя в одиночку, и их коалиция, таковы:

, ,

Лемма 1. а) , б) .

Пусть . Для max .

Лемма 2. а) , б) .

Сложив два очевидных неравенства и , получим . Теперь применим лемму 1а. Для max аналогично.

Лемма 3. , .

Лемма 4. .

Сложив два неравенства и , получим . Лемма 2б здесь неприменима, т.к. в ней стоит знак «меньше». Однако первое слагаемое справа не зависит от z, а второе от y. Дважды применив леммы 1б и 3, получим утверждение леммы 4.

Теорема. В коалицию вступать выгоднее, чем играть против всех: υ_w ≥ υ_y + υ_z.

Имеем f_w(x,w) = f_y(x,y,z) + f_z(x,y,z). Взяв от суммы сначала min по x (лемма 2а), а затем max по y, z (леммы 1б и 4), получим утверждение теоремы.

Всего в игре n лиц существует 2ⁿ коалиций. Пусть SN={1, 2,…, n}. Рассмотрим игру двух коалиций S и N\S. Выигрыш коалиции S определим так: . Легко показать, что .

Def: Говорят, что коалиционная игра задана в редуцированной форме, если задана произвольная функция : 2^N, обладающая свойствами:

1) ()=0; 2) если S₁S₂=, то (S₁+S₂)(S₁)+(S₂).

Def: Коалиционная игра существенна, если (N)>({i}).

Если игра несущественна, то создавать коалиции не имеет смысла.

Def. Игра называется простой, если выигрыш любой коалиции равен 0 или 1.

Игрок i называется болваном, если, присоединяясь к любой коалиции S, он ничего ей не приносит (т.е. v(S) = v(S \ {i})). Очевидно, что его вес _i()=0.

Def: Коалиционная игра имеет постоянную сумму, если (S)+ (N\S)=C SN.

Пример К1. Есть 3 игрока, ({i})=2 i, ({1,2})=({1,3})=({2,3})=2, ({1,2,3})=(0)=0. Это игрa с нулевой суммой.